In a rectangle, if the length is increased by 3 meters and breadth is decreased by 4 meters,
Rectangle Area Word Problem demonstrates how to form and solve a pair of linear equations from changes in a rectangle’s dimensions and area, yielding the original dimensions as 28 m × 19 m.
What Is This Problem About?
Word problems based on rectangles are a staple of Class 10 Maths Chapter 3 — Pair of Linear Equations in Two Variables. They test whether students can translate real-world geometric conditions into algebraic equations and solve them systematically.This particular problem is a classic two-variable setup: you are given two different scenarios where the length and breadth of a rectangle are modified, and the resulting change in area is known. Your job is to find the original dimensions.
Problems like this appear regularly in CBSE board exams, state board papers, and JEE Foundation assessments. Mastering them builds the algebraic thinking needed for harder coordinate geometry and calculus topics later.For more problems of this type with detailed solutions, explore NCERT Solutions for Class 10 Maths — fully solved by eSaral's IIT Bombay faculty.
The method used here — cross-multiplication — is one of the most reliable techniques for solving a 2×2 linear system and is directly tested in CBSE board exams.In a rectangle, if the length is increased by 3 meters and breadth is decreased by 4 meters, the area of the rectangle is reduced by 67 square meters. If length is reduced by 1 meter and breadth is increased by 4 meters, the area is increased by 89 Sq. meters. Find the dimensions of the rectangle.
Let the length and breadth of the rectangle be $x$ and $y$ units respectively
Then, area of rectangle $=x y$ square units
If the length is increased by 3 meters and breath is reduced each by 4 square meters the area is reduced by 67 square units
Therefore,
$x y-67=(x+3)(y-4)$
$x y-67=x y+3 y-4 x-12$
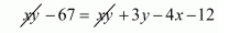
$4 x-3 y-67+12=0$
$4 x-3 y-55=0 \cdots(i)$
Then the length is reduced by 1 meter and breadth is increased by 4 meter then the area is increased by 89 square units
Therefore, $0=4 x-y-93 \cdots(i i)$
Thus, we get the following system of linear equation
$4 x-3 y-55=0$
$4 x-y-93=0$
By using cross multiplication we have
$\frac{x}{(-3 \times-93)-(-1 \times-55)}=\frac{-y}{(4 \times-93)-(4 \times-55)}=\frac{1}{(4 \times-1)-(4 \times-3)}$
$\frac{x}{279-55}=\frac{-y}{-372+220}=\frac{1}{-4+12}$
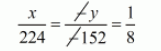
$x=\frac{224}{8}$
$x=28$
and
$y=\frac{152}{8}$
$y=19$
Hence, the length of rectangle is 28 meter,
The breath of rectangle is 19 meter.
Frequently Asked Questions
Find answers to common questions.
What is the answer to this rectangle problem?
The length of the rectangle is 28 metres and the breadth is 19 metres. These values are obtained by forming two linear equations from the two given area conditions and solving them using the cross multiplication method. Both conditions are verified: 31×15 = 465 = 532−67 ✓ and 27×23 = 621 = 532+89 ✓.
Which chapter does this problem belong to in Class 10 Maths?
This problem belongs to Chapter 3 — Pair of Linear Equations in Two Variables of the Class 10 NCERT Maths textbook. It is classified as an algebraic word problem where geometric conditions (changes in rectangle dimensions) are converted into a system of two linear equations in two unknowns.
Can this problem be solved by methods other than cross multiplication?
Yes. The same system of equations (4x − 3y = 55 and 4x − y = 93) can be solved by elimination or substitution. Subtracting equation (i) from equation (ii) gives −2y + 38 = 0 — wait, that yields 2y = 38 → y = 19 directly. Elimination is actually faster here. Cross multiplication is more general and useful for exams.
How do I form equations from rectangle area word problems?
Define length as x and breadth as y. For each condition, write: new area = original area ± change. Expand the new dimensions multiplied together, cancel the common xy term on both sides, and simplify. Each condition gives you one linear equation. Two conditions give two equations — enough to solve for both unknowns.
Why is cross-multiplication used to solve these equations?
Cross multiplication is a direct formula-based method that avoids the multi-step back-substitution required in elimination or substitution. It is particularly useful in exams when both equations are in standard form $ax + by + c = 0$. It also reduces the chance of arithmetic errors in longer coefficient sets.