In a right angle ΔABC is which ∠B = 90°,

Let O be the centre of the given circle. Suppose, the tangent at P meets BC at 0. Join BP.

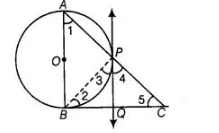
To prove   $B Q=Q C$  [angles in alternate segment]

Proot $\angle A B C=90^{\circ}$

thangent at any noint of circle is nernendicular to radius through the point of contact]

$\therefore \ln \triangle A B C$, $\angle 1+\angle 5=90^{\circ}$  [angle sum property, $\angle A B C=90^{\circ}$ ]

$\angle 3=\angle 1$

[angle between tangent and the chord equals angle made by the chord in alternate segment]

$\therefore$ $\angle 3+\angle 5=90^{\circ}$ $\ldots($ i)

Also, $\angle A P B=90^{\circ}$ [angle in semi-circle]

$\Rightarrow \quad \angle 3+\angle 4=90^{\circ}$ $\left[\angle A P B+\angle B P C=180^{\circ}\right.$, linear pair]

From Eqs. (i) and (ii), we get

$\angle 3+\angle 5=\angle 3+\angle 4$

$\Rightarrow \quad \angle 5=\angle 4$

$\Rightarrow \quad P Q=Q C$ [sides opposite to equal angles are equal]

Also, $Q P=Q B$

[tangents drawn from an internal point to a circle are equal]

$\Rightarrow \quad Q B=Q C$

Hence proved.