Question:
In Fig. 4.58, $\triangle \mathrm{ABC}$ is a triangle such that $\mathrm{ABAC}=\mathrm{BDDC}, \angle \mathrm{B}=70^{\circ}, \angle \mathrm{C}=50^{\circ}$. Find the $\angle \mathrm{BAD}$.
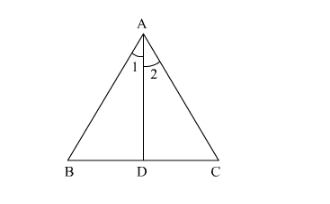
Solution:
It is given that in $\triangle A B C, \frac{A B}{A C}=\frac{B D}{D C}, \angle B=70^{\circ}$ and $\angle C=50^{\circ}$.
We have to find $\angle B A D$.
In $\triangle A B C$,
$\angle A=180^{\circ}-\left(70^{\circ}+50^{\circ}\right)$
$=180^{\circ}-120^{\circ}$
$=60^{\circ}$
Since $\frac{A B}{A C}=\frac{B D}{D C}$, therefore, $A D$ is the bisector of $\angle \mathrm{A}$.
Hence, $\angle B A D=\frac{60^{\circ}}{2}=30^{\circ}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
