Question:
In figure, BD and CE intersect each other at the point P. Is ΔPBC ~ ΔPDE? Why?
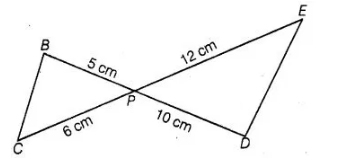
Solution:
True
$\angle B P C=\angle E P D$ [vertically opposite angles]
Now, $\frac{P B}{P D}=\frac{5}{10}=\frac{1}{2}$ $\ldots($ i)
and $\frac{P C}{P E}=\frac{6}{12}=\frac{1}{2}$ ...(ii)
From Eqs. (i) and (ii), $\frac{P B}{P D}=\frac{P C}{P E}$
Since, one angle of ΔPBC is equal to one angle of ΔPDE and the sides including these angles are proportional, so both triangles are similar.
Hence, ΔPBC ∼ ΔPDE, by SAS similarity criterion.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
