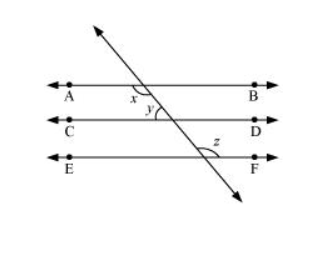
Solution:
It is given that $A B \| C D$ and $C D \| E F$
$\therefore \mathrm{AB}\|\mathrm{CD}\| \mathrm{EF}$ (Lines parallel to the same line are parallel to each other)
It can be observed that
$x=z$ (Alternate interior angles) ...(1)
It is given that $y: z=3: 7$
Let the common ratio between $y$ and $z$ be $a$.
$\therefore y=3 a$ and $z=7 a$
Also, $x+y=180^{\circ}$ (Co-interior angles on the same side of the transversal)
$z+y=180^{\circ}[U$ sing equation (1) $]$
$7 a+3 a=180^{\circ}$
$10 a=180^{\circ}$
$a=18^{\circ}$
$\therefore x=7 a=7 \times 18^{\circ}=126^{\circ}$