Prove that the sum of the squares of the sides

Solution:

ABCD is a rhombus in which AB = BC = CD = DA = a (say). Its diagonals AC and BD are right bisectors of each other at O.

In $\Delta \mathrm{OAB}, \angle \mathrm{AOB}=90^{\circ}$

$\mathrm{OA}=\frac{1}{2} \mathrm{AC}$ and $\mathrm{OB}=\frac{1}{2} \mathrm{BD}$



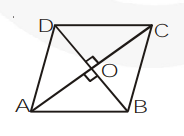
By pythagoras theorem, we have

$\mathrm{OA}^{2}+\mathrm{OB}^{2}=\mathrm{AB}^{2}$

$\Rightarrow\left(\frac{1}{2} A C\right)^{2}+\left(\frac{1}{2} B D\right)^{2}=A B^{2}$

or $4 \mathrm{AB}^{2}=\mathrm{AC}^{2}+\mathrm{BD}^{2}$

$\Rightarrow \mathrm{AB}^{2}+\mathrm{BC}^{2}+\mathrm{CD}^{2}+\mathrm{DA}^{2}$

$=\mathrm{AC}^{2}+\mathrm{BD}^{2}$

Hence proved.