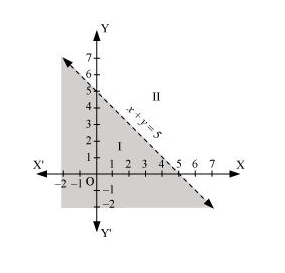
Solve the given inequality graphically in two-dimensional plane: x + y < 5

The graphical representation of x + y = 5 is given as dotted line in the figure below.

This line divides the xy-plane in two half planes, I and II.

Select a point (not on the line), which lies in one of the half planes, to determine whether the point satisfies the given inequality or not.

We select the point as (0, 0).

It is observed that,

$0+0<5$ or, $0<5$, which is true

Therefore, half plane II is not the solution region of the given inequality. Also, it is evident that any point on the line does not satisfy the given strict inequality.

Thus, the solution region of the given inequality is the shaded half plane I excluding the points on the line.

This can be represented as follows.