Question: The region represented by $|x-y| \leq 2$ and $|x+y| \leq 2$ is bounded by a :
(1) square of side length $2 \sqrt{2}$ units
(2) rhombus of side length 2 units
(c) square of area $16 \mathrm{sq}$. units
(4) rhombus of area $8 \sqrt{2}$ sq. units
Correct Option: 1
Solution:
Let, $\mathrm{C}_{1}:|y-x| \leq 2$
$\mathrm{C}_{2}:|y+x| \leq 2$
By the diagram, region is square
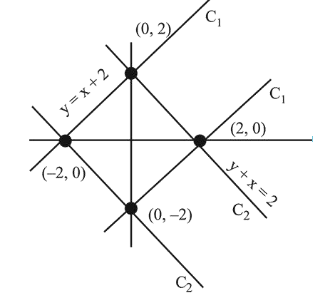
Now, length of side $=\sqrt{2^{2}+2^{2}}=2 \sqrt{2}$
