The weights of coffee in 70 jars are shown in the following table:
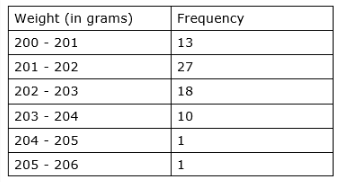
Determine variance and standard deviation of the above distribution.
Given the weights of coffee in 70 jars
Now we have to find the variance and standard deviation of the distribution
Let us make a table of the given data and append other columns after calculations
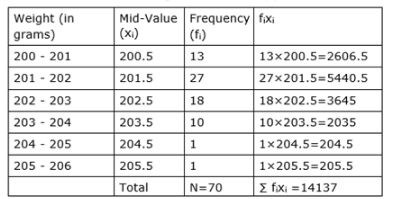
Here mean, ${ }^{\bar{x}}=\frac{\sum f_{1} x_{1}}{N}=\frac{14137}{70}=201.9$
So the above table with more columns is as shown below,
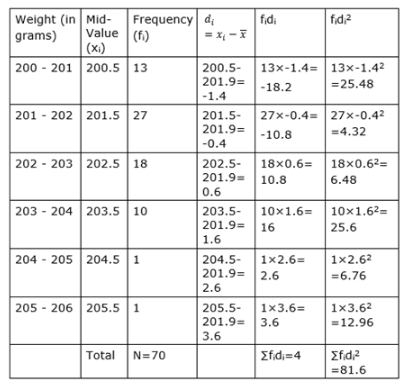
And we know standard deviation is
$\sigma=\sqrt{\frac{\sum f_{i} d_{i}^{2}}{n}-\left(\frac{\sum f_{i} d_{i}}{n}\right)^{2}}$
Substituting values from above table, we get
$\sigma=\sqrt{\frac{81.6}{70}-\left(\frac{4}{70}\right)^{2}}$
$\sigma=\sqrt{1.17-(0.057)^{2}}$
$\sigma=\sqrt{1.17-0.003249}=\sqrt{1.17}$
$\Rightarrow \sigma=1.08 \mathrm{~g}$
And $\sigma^{2}=1.08^{2}=1.17 \mathrm{~g}$
Hence the variance and standard deviation of the distribution are $1.166 \mathrm{~g}$ and $1.08$ respectively.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
