where R+ is the set of all non-negative real numbers.

Solution:

$f: \mathbf{R}_{+} \rightarrow[4, \infty)$ is given as $f(x)=x^{2}+4$

One-one:

Let f(x) = f(y).

$\Rightarrow x^{2}+4=y^{2}+4$

$\Rightarrow x^{2}=y^{2}$

$\Rightarrow x=y \quad\left[\right.$ as $\left.x=y \in \mathbf{R}_{+}\right]$

∴ f is a one-one function.

Onto:

For $y \in[4, \infty)$, let $y=x^{2}+4$

$\Rightarrow x^{2}=y-4 \geq 0 \quad[$ as $y \geq 4]$

$\Rightarrow x=\sqrt{y-4} \geq 0$

Therefore, for any $y \in \mathbf{R}$, there exists $x=\sqrt{y-4} \in \mathbf{R}$ such that

$f(x)=f(\sqrt{y-4})=(\sqrt{y-4})^{2}+4=y-4+4=y$

∴ f is onto.

Thus, $f$ is one-one and onto and therefore, $f^{-1}$ exists.

Let us define $g:[4, \infty) \rightarrow \mathbf{R}_{+}$by,

$g(y)=\sqrt{y-4}$

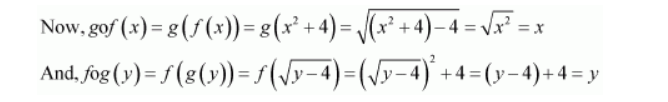
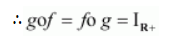
Hence, f is invertible and the inverse of f is given by

$f^{-1}(y)=g(y)=\sqrt{y-4}$