Draw the graphs of the lines x – y = 1 and 2x + y = 8. Shade the area formed by these two lines and the y-axis.
The lines x – y = 1 and 2x + y = 8 form a triangle with the y-axis, and the bounded area is 27/2 square units.
Draw the graphs of the lines x – y = 1 and 2x + y = 8. Shade the area formed by these two lines and the y-axis. Also, find this area.
$x-y=1$
$\Rightarrow y=x-1$
When $x=0, y=0-1=-1$
When $x=1, y=1-1=0$
When $x=2, y=2-1=1$
Thus, the points on the line x – y = 1 are as given in the following table:
Plotting the points (0, –1), (1, 0) and (2, 1) and drawing a line passing through these points, we obtain the graph of of the line x – y = 1.
$2 x+y=8$
$\Rightarrow y=-2 x+8$
When $x=1, y=-2 \times 1+8=-2+8=6$
When $x=2, y=-2 \times 2+8=-4+8=4$
When $x=3, y=-2 \times 3+8=-6+8=2$
Thus, the points on the line 2x + y = 8 are as given in the following table:
Plotting the points (1, 6), (2, 4) and (3, 2) and drawing a line passing through these points, we obtain the graph of of the line 2x + y = 8.
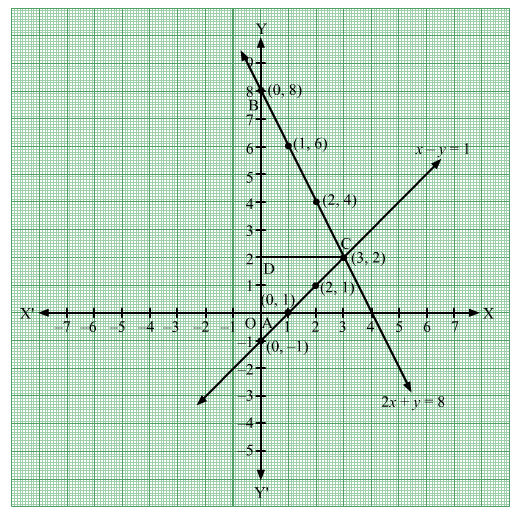
The shaded region represents the area bounded by the lines x – y = 1, 2x + y = 8 and the y-axis. This represents a triangle.
It can be seen that the lines intersect at the point C(3, 2). Draw CD perpendicular from C on the y-axis.
Height = CD = 3 units
Base = AB = 9 units
$\therefore$ Area of the shaded region $=$ Area of $\Delta \mathrm{ABC}=\frac{1}{2} \times \mathrm{AB} \times \mathrm{CD}=\frac{1}{2} \times 9 \times 3=\frac{27}{2}$ square units
🚀 Checkout eSaral Courses
Frequently Asked Questions
Find answers to common questions.
What are the vertices of the triangle formed by x – y = 1, 2x + y = 8, and the y-axis?
The three vertices are A(0, 8), B(0, –1), and C(3, 2). A and B are the y-intercepts of the two lines respectively, and C is the point where the two lines intersect each other. You can verify each vertex by substituting into the original equations.
What is the area of the triangle formed by the lines x – y = 1 and 2x + y = 8 and the y-axis?
The area is 27/2 square units (13.5 sq. units). The base AB = 9 units lies along the y-axis, and the perpendicular height CD = 3 units is the horizontal distance from the intersection point C(3, 2) to the y-axis. Applying Area = ½ × base × height gives ½ × 9 × 3 = 13.5.
How do you find where the lines x – y = 1 and 2x + y = 8 intersect?
Solve the two equations simultaneously. From x – y = 1, write x = y + 1. Substitute into 2x + y = 8 to get 2(y+1) + y = 8, which gives 3y = 6, so y = 2 and x = 3. The intersection point is (3, 2). Always verify by substituting back into both equations.
Why does the shaded region form a triangle and not another shape?
Two straight lines and the y-axis create exactly three boundary lines. Three non-parallel, non-concurrent lines always enclose a triangular region. In this problem, the y-axis and the two given lines meet at three distinct points — A, B, and C — forming a triangle.
How do you find the y-intercepts of x – y = 1 and 2x + y = 8?
Set x = 0 in each equation. For x – y = 1: 0 – y = 1, so y = –1, giving point B(0, –1). For 2x + y = 8: 0 + y = 8, so y = 8, giving point A(0, 8). These two y-intercepts, along with the intersection point C(3, 2), are the three vertices of the triangle.