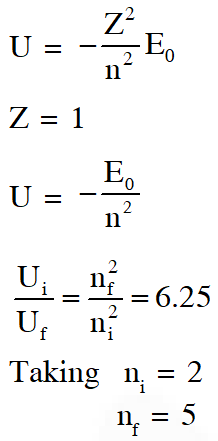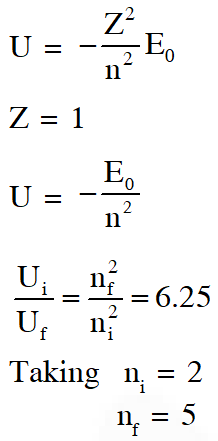JEE Advanced Previous Year Questions of Physics with Solutions are available at eSaral. Practicing JEE Advanced Previous Year Papers Questions of Physics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
Get detailed Class 11th & 12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Click Here for JEE main Previous Year Topic Wise Questions of Physics with Solutions
Download eSaral app for free study material and video tutorials.
Simulator
Previous Years JEE Advanced Questions
Paragraph for Question Nos. 1 to 3
The key feature of Bohr’s theory of spectrum of hydrogen atom is the quantization of angular momentum when an electron is revolving around a proton. We will extend this to a general rotational motion to find quantized rotational energy of a diatomic molecule assuming it to be rigid. The rule to be applied is Bohr’s quantization condition.
Simulator
Previous Years JEE Advanced Questions
Paragraph for Question Nos. 1 to 3
The key feature of Bohr’s theory of spectrum of hydrogen atom is the quantization of angular momentum when an electron is revolving around a proton. We will extend this to a general rotational motion to find quantized rotational energy of a diatomic molecule assuming it to be rigid. The rule to be applied is Bohr’s quantization condition.
Q. A diatomic molecule has moment of inertia I. By Bohr’s quantization condition its rotational energy in the nth level (n =0 is not allowed) is
$(\mathrm{A}) \frac{1}{\mathrm{n}^{2}}\left(\frac{\mathrm{h}^{2}}{8 \pi^{2} \mathrm{I}}\right)$
$(\mathrm{B}) \frac{1}{\mathrm{n}}\left(\frac{\mathrm{h}^{2}}{8 \pi^{2} \mathrm{I}}\right)$
$(\mathrm{C}) \mathrm{n}\left(\frac{\mathrm{h}^{2}}{8 \pi^{2} \mathrm{I}}\right)$
$(\mathrm{D}) \mathrm{n}^{2}\left(\frac{\mathrm{h}^{2}}{8 \pi^{2} \mathrm{I}}\right)$
[JEE 2010]
Ans. (D)
$\mathrm{E}_{\mathrm{n}}=\frac{1}{2} \mathrm{I} \omega^{2}=\frac{(\mathrm{l} \omega)^{2}}{2 \mathrm{l}}=\frac{(\mathrm{nh} / 2 \pi)^{2}}{2 \mathrm{l}}=\frac{\mathrm{n}^{2} \mathrm{h}^{2}}{8 \pi^{2} \mathrm{I}}$
Q. It is found that the excitation frequency from ground to the first excited state of rotation for the CO molecule is close to $\frac{4}{\pi} \times 10^{11} \mathrm{Hz}$ Hz. Then the moment of inertia of CO molecule about its center of mass is close to $\left[\text { Take } \mathrm{h}=2 \pi \times 10^{-34} \mathrm{Js}\right)$
(A) $2.76 \times 10^{-46} \mathrm{kg} \mathrm{m}^{2}$
(B) $1.87 \times 10^{-46} \mathrm{kg} \mathrm{m}^{2}$
(C) $4.67 \times 10^{-47} \mathrm{kg} \mathrm{m}^{2}$
(D) $1.17 \times 10^{-47} \mathrm{kg} \mathrm{m}^{2}$
[JEE 2010]
Ans. (B)
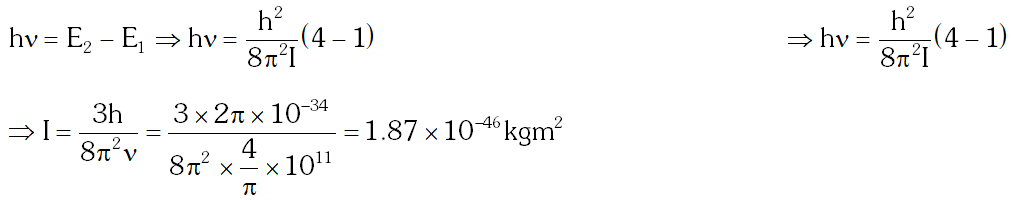
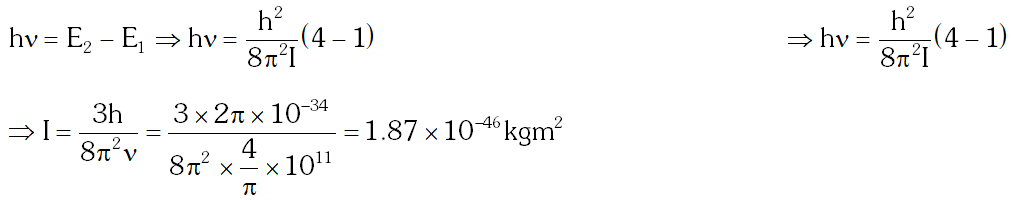
Q. In a CO molecule, the distance between C (mass = 12 a.m.u.) and O (mass = 16 a.m.u.), where 1 a.m.u. $=\frac{5}{3} \times 10^{-27} \mathrm{kg},$ is close to
(A) $2.4 \times 10^{-10} \mathrm{m}$
(B) $1.9 \times 10^{-10} \mathrm{m}$
(C) $1.3 \times 10^{-10} \mathrm{m}$
(D) $4.4 \times 10^{-11} \mathrm{m}$
[JEE 2010]
Ans. (C)
Moment of inertia of CO molecule about centre of mass : $\mathrm{I}=\mu \mathrm{r}^{2}$ where $\mu=\frac{\mathrm{m}_{1} \mathrm{m}_{2}}{\mathrm{m}_{1}+\mathrm{m}_{2}}$
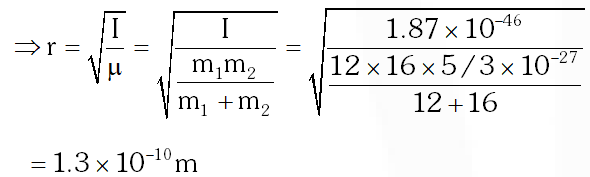
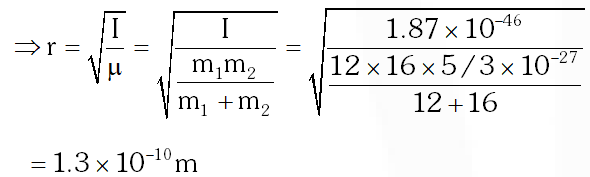
Q. The wavelength of the first spectral line in the Balmer series of hydrogen atom is 6561 Å. The wavelength of the second spectral line in the Balmer series of singly-ionized helium atom is ?
[JEE 2011]
[JEE 2011]
Ans. (A)
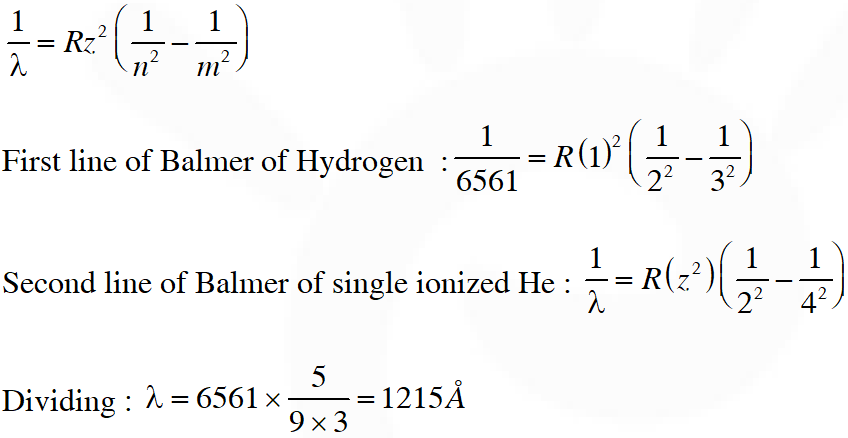
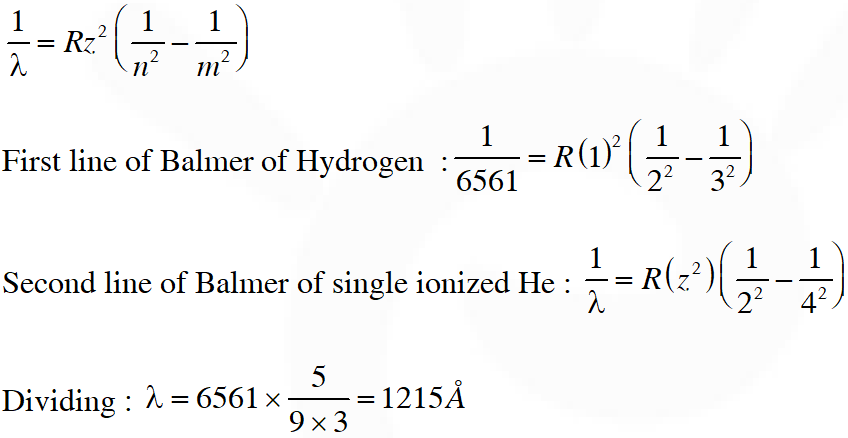
Q. The radius of the orbit of an electron in a Hydrogen-like atom is 4.5 a0, where a0 is the Bohr radius. Its orbital angular momentum is $\frac{3 \mathrm{h}}{2 \pi}$. It is given that h is Planck constant and R is Rydberg constant. The possible wavelength (s), when the atom de-excites, is (are) :-
(A) $\frac{9}{32 \mathrm{R}}$
(B) $\frac{9}{16 \mathrm{R}}$
(C) $\frac{9}{\text { sR }}$
(D) $\frac{4}{3 \mathrm{R}}$
[JEE Advanced-2013]
Ans. (A,C)
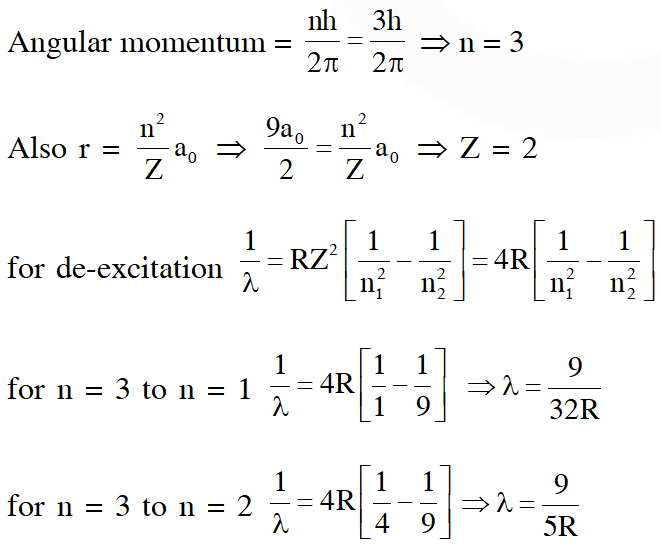for $\mathrm{n}=2$ to $\mathrm{n}=1 \quad \frac{1}{\lambda}=4 \mathrm{R}\left[\frac{1}{1}-\frac{1}{4}\right] \Rightarrow \lambda=\frac{3}{\mathrm{R}}$
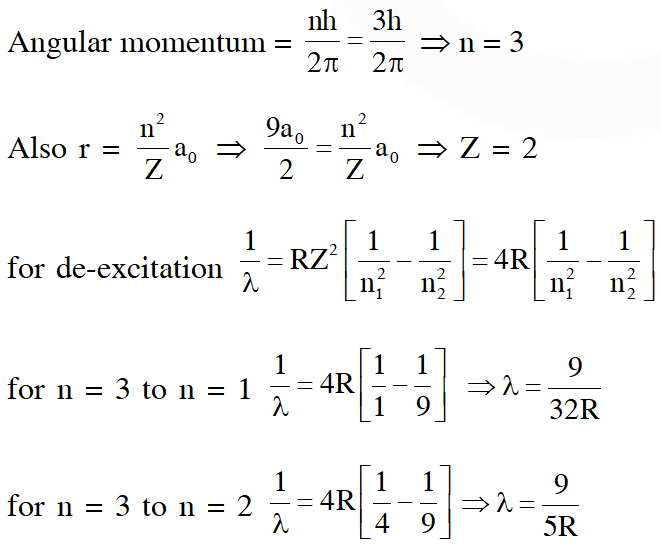for $\mathrm{n}=2$ to $\mathrm{n}=1 \quad \frac{1}{\lambda}=4 \mathrm{R}\left[\frac{1}{1}-\frac{1}{4}\right] \Rightarrow \lambda=\frac{3}{\mathrm{R}}$
Q. Consider a hydrogen atom with its electron in the nth orbital. An electromagnetic radiation of wavelength 90 nm is used to ionize the atom. If the kinetic energy of the ejected electron is 10.4 eV, then the value of n is (hc = 1242 eV nm).
[JEE Advanced-2015]
Ans. 2
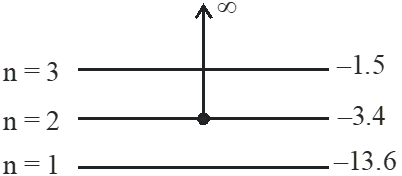$\mathrm{E}_{\mathrm{Ph}}=\frac{\mathrm{hc}}{\lambda}=\frac{1242}{90}=13.8 \mathrm{eV}$
$\mathrm{E}_{\mathrm{Ph}}=\Delta \mathrm{E}+(\mathrm{K.E.})$
$13.8=\Delta \mathrm{E}+10.4$
$\Delta E=3.4 \mathrm{eV}$
so electron initially was in n = 2
$\mathrm{E}_{\mathrm{Ph}}=\frac{\mathrm{hc}}{\lambda}=\frac{1242}{90}=13.8 \mathrm{eV}$
$\mathrm{E}_{\mathrm{Ph}}=\Delta \mathrm{E}+(\mathrm{K.E.})$
$13.8=\Delta \mathrm{E}+10.4$
$\Delta E=3.4 \mathrm{eV}$
so electron initially was in n = 2
Q. Highly excited states for hydrogen like atoms (also called Rydberg states) with nuclear charge Ze are defined by their principal quantum number n, where n >> 1. Which of the following statement(s) is (are) true?
(A) Relative change in the radii of two consecutive orbitals does not depend on Z
(B) Relative change in the radii of two consecutive oribitals varies as 1/n
(C) Relative change in the energy of two consecutive orbitals varies as $1 / \mathrm{n}^{3}$
(D) Relative change in the angular momenta of two consecutive orbitals varies as 1/n
[JEE Advanced-2016]
Ans. (A,B,D)
As radius $\mathrm{r} \propto \frac{\mathrm{n}^{2}}{\mathrm{z}}$
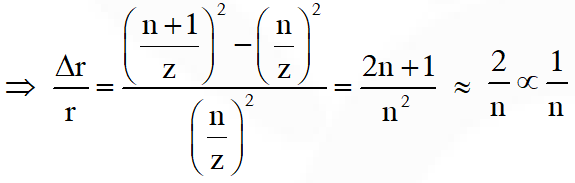as energy $\mathrm{E} \propto \frac{\mathrm{z}^{2}}{\mathrm{n}^{2}}$
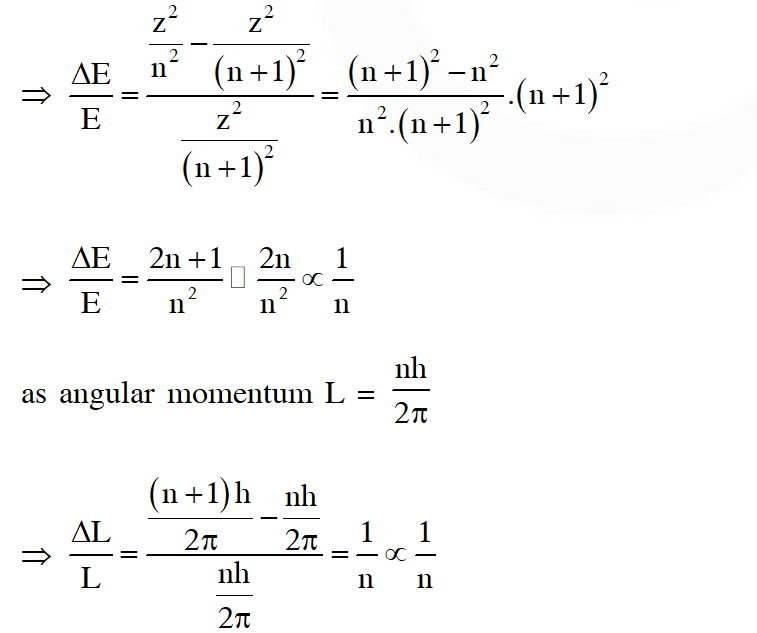
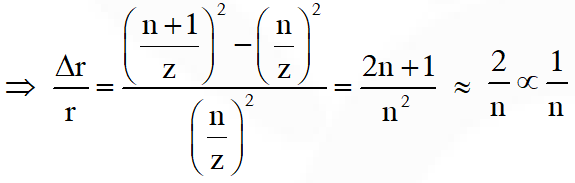as energy $\mathrm{E} \propto \frac{\mathrm{z}^{2}}{\mathrm{n}^{2}}$
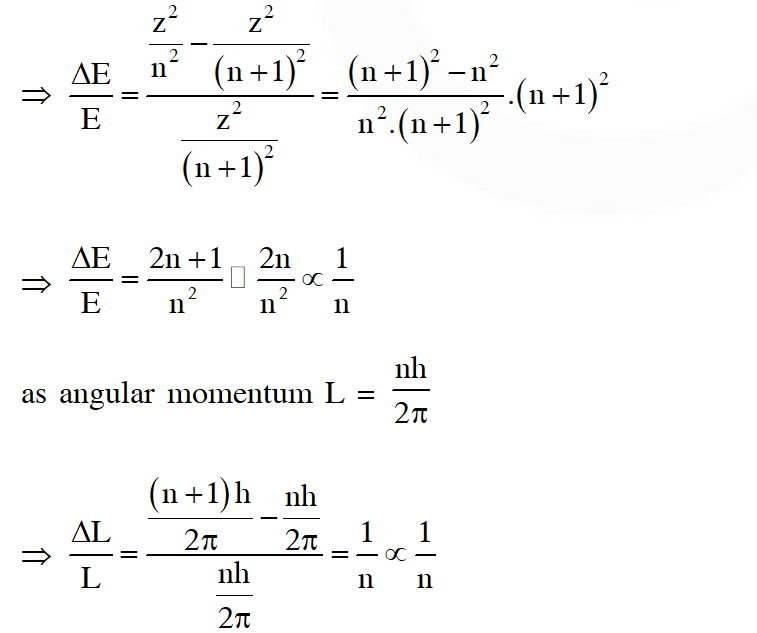
Q. A hydrogen atom in its ground state is irradiated by light of wavelength 970 $\hat{\mathbf{A}}$. Taking
hc/e = $1.237 \times 10^{-6}$ eV m and the ground state energy of hydrogen atom as –13.6 eV, the number of lines present in the emission spectrum is ?
[JEE Advanced-2016]
Ans. 6
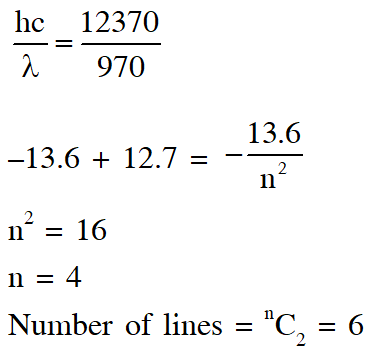
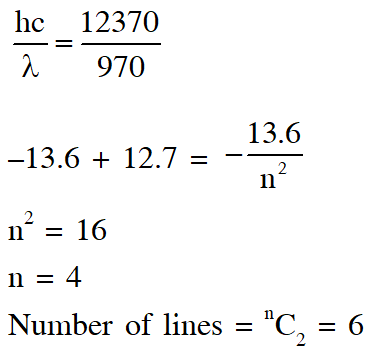
Q. An electron in a hydrogen atom undergoes a transition from an orbit with quantum number $\mathrm{n}_{\mathrm{i}}$ to another with quantum number $\mathrm{n}_{\mathrm{f}} \cdot \mathrm{V}_{\mathrm{i}}$ and $\mathrm{V}_{\mathrm{f}}$ are respectively the initial and final potential energies of the electron. If $\frac{\mathrm{V}_{\mathrm{i}}}{\mathrm{V}_{\mathrm{f}}}=6.25$, then the smallest possible $\mathbf{n}_{\mathrm{f}}$ is.
[JEE Advanced-2017]
Ans. 5
