JEE Main Previous Year Question of Math with Solutions are available at eSaral. Practicing JEE Main Previous Year Papers Questions of mathematics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
Get detailed Class 11th &12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Q. The remainder left out when $8^{2 n}-(62)^{2 n+1}$ is divided by 9 is :-
(1) 7 (2) 8 (3) 0 (4) 2
[AIEEE 2009]
Ans. (4)
$8^{2 \mathrm{n}}-(62)^{2 \mathrm{n}+1}$
$=(63+1)^{\mathrm{n}}-(63-1)^{2 \mathrm{n}+1}$
$=\left(63 \mathrm{I}_{1}+1\right)-\left(63 \mathrm{I}_{2}-1\right)$
$=63 \mathrm{I}_{3}+2=9 \mathrm{I}+2$
Q. Let $S_{1}=\sum_{j=1}^{10} j(j-1)^{10} C_{j}, S_{2}=\sum_{j=1}^{10} j^{10} C_{j}$ and $S_{3}=\sum_{j=1}^{10} j^{20} C_{j}$
Statement-1: $S_{3}=55 \times 2^{9}$.
Statement-2 : $S_{1}=90 \times 2^{8}$ and $S_{2}=10 \times 2^{8}$.
(1) Statement–1 is true, Statement–2 is true ; Statement–2 is a correct explanation for Statement–1.
(2) Statement–1 is true, Statement–2 is true ; Statement–2 is not a correct explanation for Statement–1.
`(3) Statement–1 is true, Statement–2 is false.
(4) Statement–1 is false, Statement–2 is true.
[AIEEE-2010]
Ans. (3)
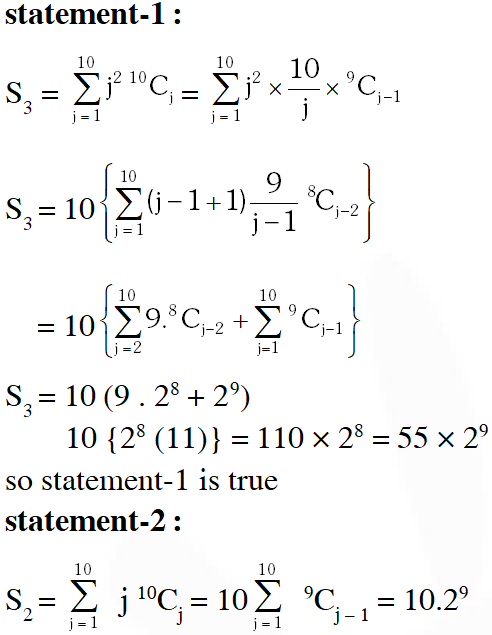so, statement-2 is wrong.
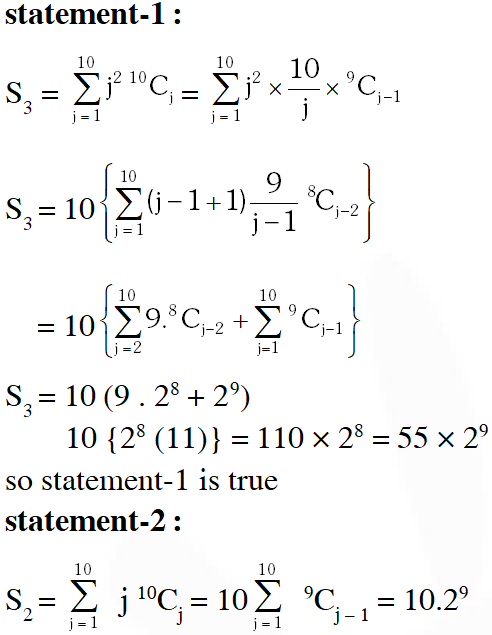so, statement-2 is wrong.
Q. The coefficient of $x^{7}$ in the expansion of $\left(1-x-x^{2}+x^{3}\right)^{6}$ is :-
(1) – 144 (2) 132 (3) 144 (4) – 132
[AIEEE 2011]
Ans. (1)
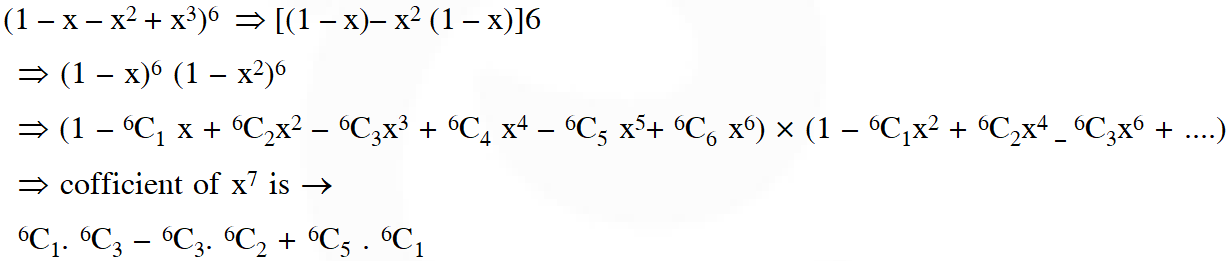
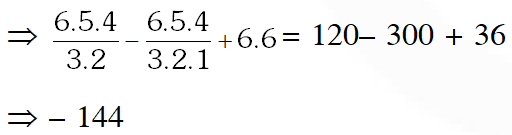
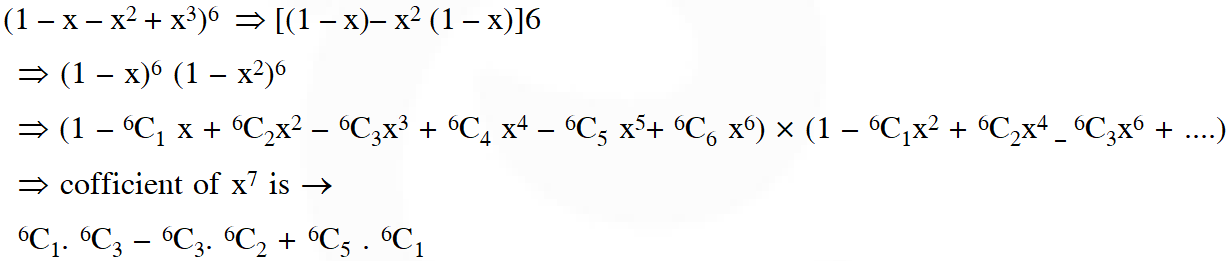
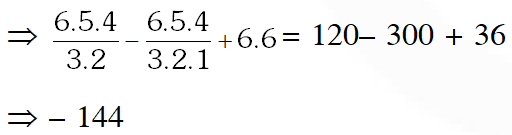
Q. If $\mathrm{n}$ is a positive integer, then $(\sqrt{3}+1)^{2 \mathrm{n}}-(\sqrt{3}-1)^{2 \mathrm{n}}$ is :
(1) a rational number other than positive integers
(2) an irrational number
(3) an odd positive integer
(4) an even positive integer
[AIEEE 2012]
Ans. (2)
$(\sqrt{3}+1)^{2 n}-(\sqrt{3}-1)^{2 n}$
$=2\left[\mathrm{T}_{2}+\mathrm{T}_{2}+\mathrm{T}_{6}+\ldots \ldots+\mathrm{T}_{2 \mathrm{n}}\right]$
$=2\left[2 \mathrm{n} \mathrm{C}_{1}(\sqrt{3})^{2 n-1}+2 \mathrm{n} \mathrm{C}_{3}(\sqrt{3})^{2 \mathrm{n}-3}+\ldots \ldots \ldots\right]$
$=$ An Irrational Number
Q. The term independent of $x$ in expansion of $\left(\frac{x+1}{x^{2 / 3}-x^{1 / 3}+1}-\frac{x-1}{x-x^{1 / 2}}\right)^{10}$ is :
(1) 4 (2) 120 (3) 210 (4) 310
[JEE-Main 2013]
Ans. (3)
$\left(\frac{x+1}{x^{2 / 3}-x^{1 / 3}+1}-\frac{x-1}{x-\sqrt{x}}\right)^{10}$
$\left(\mathrm{x}^{1 / 3}+1-\left(\frac{\sqrt{\mathrm{x}}+1}{\sqrt{\mathrm{x}}}\right)\right)^{10}$
$\left(\mathrm{x}^{1 / 3}-\mathrm{x}^{-1 / 2}\right)^{10}$
$\mathrm{T}_{\mathrm{r}+1}=^{10} \mathrm{C}_{\mathrm{r}}\left(\mathrm{x}^{1 / 3}\right)^{10-\mathrm{r}}\left(\mathrm{x}^{-1 / 2}\right)^{\mathrm{r}}$
$\frac{10-r}{3}-\frac{r}{2}=0$
20 – 2r = 3r
r = 4
$\mathrm{T}_{5}=\mathrm{T}_{4+1}=^{10} \mathrm{C}_{4}=\frac{10 !}{6 ! .4 !}=210$
Q. If the coefficients of $x^{3}$ and $x^{4}$ in the expansion of $\left(1+a x+b x^{2}\right)(1-2 x)^{18}$ in powers of $x$ are both zero, then $(a, b)$ is equal to :-
( 1)$\left(16, \frac{251}{3}\right)$
(2) $\left(14, \frac{251}{3}\right)$
(3) $\left(14, \frac{272}{3}\right)$
( 4)$\left(16, \frac{272}{3}\right)$
[JEE(Main)-2014]
Ans. (4)
In the expansion of $\left(1+a x+b x^{2}\right)(1-2 x)^{18}$
General term $=\left(1+a x+b x^{2}\right) \cdot 18 C_{r}(-2 x)^{r}$
Cofficinet of
$x^{3}=18 C_{3}(-2)^{3}+a \cdot\left(8 C_{2}(-2)^{2}+b \cdot 18 C_{1}(-2)=0\right.$
Cofficinet of
$\mathrm{x}^{4}=18 \mathrm{C}_{4}(-2)^{4}+\mathrm{a} \cdot^{18} \mathrm{C}_{3}(-2)^{3}+\mathrm{b} \cdot 18 \mathrm{C}_{2}(-2)^{2}=0$
on solving the equations we get
$153 \mathrm{a}-9 \mathrm{b}=1632 \quad \ldots$ (i)
$3 \mathrm{b}-32 \mathrm{a}=-240 \quad \ldots$ (ii)
on solving we get $a=16 \& b=\frac{272}{3}$
Q. The sum of coefficients of integral powers of $x$ in the binomial expansion of $(1-2 \sqrt{x})^{50}$ is :
(1) $\frac{1}{2}\left(3^{50}-1\right)$
(2) $\frac{1}{2}\left(2^{50}+1\right)$
(3) $\frac{1}{2}\left(3^{50}+1\right)$
( 4)$\frac{1}{2}\left(3^{50}\right)$
[JEE(Main)-2015]
Ans. (3)
$\because(1-2 \sqrt{\mathrm{x}})^{50}=50 \mathrm{C}_{0}-^{50} \mathrm{C}_{1}(2 \sqrt{\mathrm{x}})+50 \mathrm{C}_{2}(2 \sqrt{\mathrm{x}})^{2}+\ldots \ldots+50 \mathrm{C}_{50}(2 \sqrt{\mathrm{x}})^{50}$
$\therefore$ consider $(1+2 \sqrt{\mathrm{x}})^{50}=50 \mathrm{C}_{0}+^{50} \mathrm{C}_{1}(2 \sqrt{\mathrm{x}})+\ldots \ldots+50 \mathrm{C}_{50}(2 \sqrt{\mathrm{x}})^{50}$
add both equations and put $\mathrm{x}=1$
$\Rightarrow \mathrm{sum}$ of coefficients of integral powers of
$\mathrm{x}=\frac{1}{2}\left(1+3^{50}\right)$
Q. If the number of terms in the expansion of
$\left(1 \frac{2}{x}+\frac{4}{x^{2}}\right)^{n}, x \neq 0,$ is $28,$ then the sum of the
coefficients of all the terms in this expansion, is :-
(1) 729 (2) 64 (3) 2187 (4) 243
[JEE(Main)-2016]
Ans. (1 or bonus)
Number of terms in the expansion of
$\left(1-\frac{2}{x}+\frac{4}{x^{2}}\right)^{n}$ is $^{n}+2 C_{2}$ (considering $\frac{1}{x}$ and $\frac{1}{x^{2}}$ distinct)
$\therefore n+2 C_{2}=28 \Rightarrow n=6$
$\therefore$ Sum of coefficients $=(1-2+4)^{6}=729$
But number of dissimilar terms actually will be $2 n+1$
(as $\frac{1}{x}$ and $\frac{1}{x^{2}}$ are functions as same variable)
Hence it contains error, so a bonus can be expected.
Q. The value of
$\left(21 \mathrm{C}_{1}-10 \mathrm{C}_{1}\right)+\left(21 \mathrm{C}_{2}-^{10} \mathrm{C}_{2}\right)+$
$\left(^{21} \mathrm{C}_{3}-^{10} \mathrm{C}_{3}\right)+\left(21 \mathrm{C}_{4}-^{10} \mathrm{C}_{4}\right)+\ldots .+$
$\left(^{21} \mathrm{C}_{10}-^{10} \mathrm{C}_{10}\right)$ is
(1) $2^{20}-2^{10}$
(2) $2^{21}-2^{11}$
(3) $2^{21}-2^{10}$
(4) $2^{20}-2^{9}$
[JEE(Main)-2017]
Ans. (1)
$\left(^{21} \mathrm{C}_{1}+^{21} \mathrm{C}_{2} \ldots \ldots \ldots+210\right.$
$-\left(^{10} \mathrm{C}_{1}+^{10} \mathrm{C}_{2} \ldots \ldots \ldots .^{10} \mathrm{C}_{10}\right)$
$=\frac{1}{2}\left[\left(^{(21} \mathrm{C}_{1}+\ldots .+^{21} \mathrm{C}_{10}\right)+\left(^{21} \mathrm{C}_{11}+\ldots .2^{21} \mathrm{C}_{20}\right)\right]-\left(2^{10}-1\right)$
$=\frac{1}{2}\left[2^{21}-2\right]-\left(2^{10}-1\right)$
$=\left(2^{20}-1\right)-\left(2^{10}-1\right)=2^{20}-2^{10}$
Q. The sum of the co-efficients of all odd degree terms in the expansion of $(x+\sqrt{x^{3}-1})^{5}+$ $(x-\sqrt{x^{3}-1})^{5},(x>1)$ is-
(1) 0 (2) 1 (3) 2 (4)
Ans. (3)
using $(x+a)^{5}+(x-a)^{5}$
$=2\left[^{5} C_{0} x^{5}+^{5} C_{2} x^{3} \cdot a^{2}+^{5} C_{4} x \cdot a^{4}\right]$
$(x+\sqrt{x^{3}-1})^{5}+(x-\sqrt{x^{3}-1})^{5}$
$=2\left[^{5} C_{0} x^{5}+^{5} C_{2} x^{3}\left(x^{3}-1\right)+^{5} C_{4} x\left(x^{3}-1\right)^{2}\right]$
$\Rightarrow 2\left[x^{5}+10 x^{6}-10 x^{3}+5 x^{7}-10 x^{4}+5 x\right]$
considering odd degree terms,
$\quad 2\left[x^{5}+5 x^{7}-10 x^{3}+5 x\right]$
$\therefore$ Sum of coefficients of odd terms is 2
Comments
Gaurav Kumar Patel
Aug. 20, 2020, 8:12 p.m.
It's really very helpful in last 20 day prepration. In few questions whole concept of a chapter is covered and pattern is also clear about exam.
It's really beneficial for me.