JEE Main Previous Year Question of Physics with Solutions are available here. Practicing JEE Main Previous Year Papers Questions of Physics will help all the JEE aspirants in realizing the question pattern as well as help in analyzing their weak & strong areas.
Get detailed Class 11th &12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Simulator
Previous Years AIEEE/JEE Mains Questions
Q. Consider a rubber ball freely falling from a height h = 4.9 m onto a horizontal elastic plate. Assume that the duration of collision is negligible and the collision with the plate is totally elastic. Then the velocity as a function of time and the height as a function of time will be :-
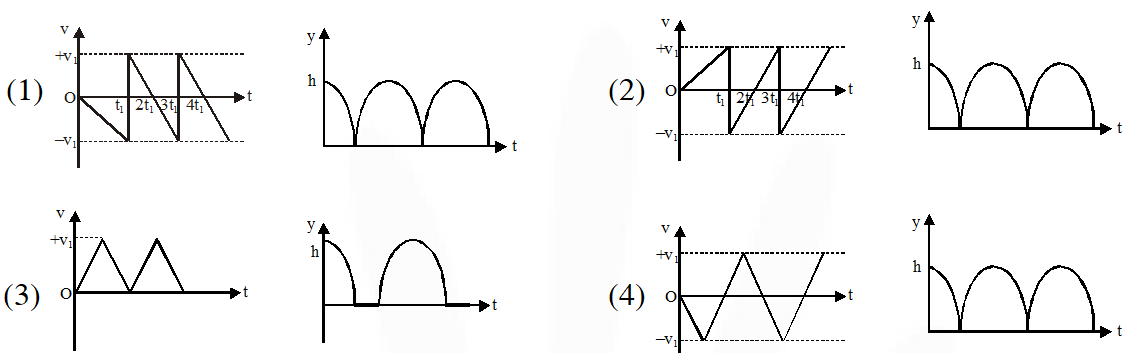 Directions : Question number 9 contain Statement-1 and Statement-2. Of the four choices given after the statements, choose the one that best discribes the two statements.
[AIEEE - 2009]
Directions : Question number 9 contain Statement-1 and Statement-2. Of the four choices given after the statements, choose the one that best discribes the two statements.
[AIEEE - 2009]
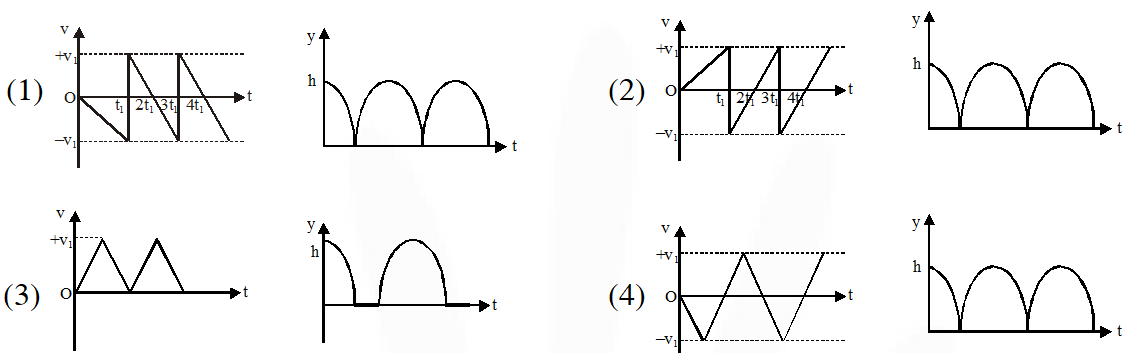 Directions : Question number 9 contain Statement-1 and Statement-2. Of the four choices given after the statements, choose the one that best discribes the two statements.
[AIEEE - 2009]
Directions : Question number 9 contain Statement-1 and Statement-2. Of the four choices given after the statements, choose the one that best discribes the two statements.
[AIEEE - 2009]
Ans. (1)
Q. Statement-1 : Two particles moving in the same direction do not lose all their energy in a completely inelastic collision.
Statement-2 : Principle of conservation of momentum holds true for all kinds of collisions.
(1) Statement–1 is true, Statement–2 is false
(2) Statement–1 is true, Statement–2 is true; Statement–2 is the correct explanation of Statement–1
(3) Statement–1 is true, Statement–2 is true; Statement–2 is not the correct explanation
of Statement–1
(4) Statement–1 is false, Statement–2 is true
[AIEEE - 2010]
Ans. (2)
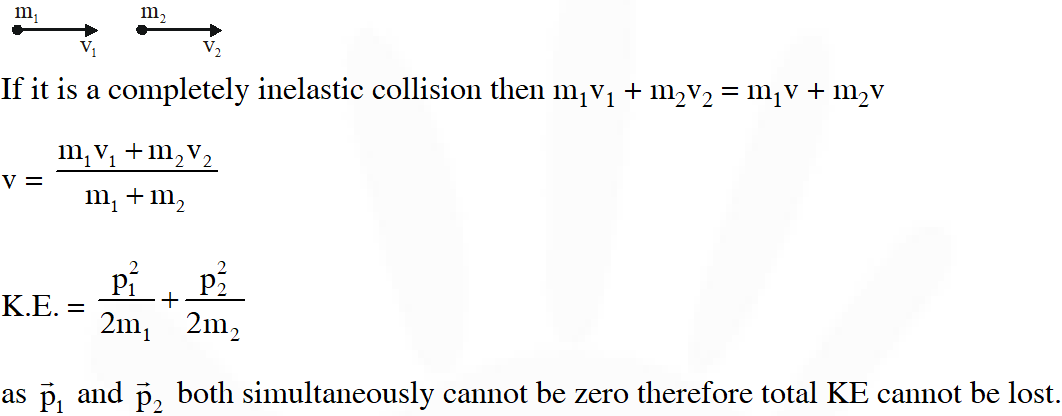
Q. This question has Statement I and Statement II. Of the four choices given after the Statements, choose the one that best describes the two Statements.
Statement - I : A point particle of mass m moving with speed v collides with stationary point particle of mass M. If the maximum energy loss possible is given as $\mathrm{f}\left(\frac{1}{2}\mathrm{mv}^{2}\right)$then$\mathrm{f}=\left(\frac{\mathrm{m}}{\mathrm{M}+\mathrm{m}}\right)$
Statement - II : Maximum energy loss occurs when the particles get stuck together as a result of the collision.
(1) Statement–I is true, Statement–II is true, Statement–II is a correct explanation of Statement–I.
(2) Statement–I is true, Statement–II is true, Statement–II is a not correct explanation of
Statement–I.
(3) Statement–I is true, Statement–II is false.
(4) Statement–I is false, Statement–II is true
[JEE Mains-2013]
Ans. (4)
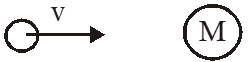 Energy loss will be maximum when collision will be perfectly inelastic
Energy loss will be maximum when collision will be perfectly inelastic
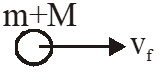 (By momentum)
Maximum energy loss $=\mathrm{K}_{\mathrm{i}}-\mathrm{K}_{\mathrm{f}}$
$=\frac{1}{2} \mathrm{mv}^{2}-\frac{1}{2}(\mathrm{m}+\mathrm{M}) \mathrm{v}_{\mathrm{f}}^{2}$
$=\frac{1}{2} \mathrm{mv}^{2}-\frac{1}{2}(\mathrm{m}+\mathrm{M}) \frac{\mathrm{m}^{2} \mathrm{v}^{2}}{(\mathrm{m}+\mathrm{M})^{2}}$
$=\frac{1}{2} \mathrm{mv}^{2}\left[1-\frac{\mathrm{m}}{\mathrm{m}+\mathrm{M}}\right]$
$=\left(\frac{\mathrm{M}}{\mathrm{m}+\mathrm{M}}\right) \frac{1}{2} \mathrm{mv}^{2}$
statement 1 is false.
(By momentum)
Maximum energy loss $=\mathrm{K}_{\mathrm{i}}-\mathrm{K}_{\mathrm{f}}$
$=\frac{1}{2} \mathrm{mv}^{2}-\frac{1}{2}(\mathrm{m}+\mathrm{M}) \mathrm{v}_{\mathrm{f}}^{2}$
$=\frac{1}{2} \mathrm{mv}^{2}-\frac{1}{2}(\mathrm{m}+\mathrm{M}) \frac{\mathrm{m}^{2} \mathrm{v}^{2}}{(\mathrm{m}+\mathrm{M})^{2}}$
$=\frac{1}{2} \mathrm{mv}^{2}\left[1-\frac{\mathrm{m}}{\mathrm{m}+\mathrm{M}}\right]$
$=\left(\frac{\mathrm{M}}{\mathrm{m}+\mathrm{M}}\right) \frac{1}{2} \mathrm{mv}^{2}$
statement 1 is false.
Q. A particle of mass m moving in the x direction with speed 2u is hit by another particle of mass 2m moving in the y direction with speed u. If the collisions perfectly inelastic , the percentage loss in the energy during the collision is close to :
(1) 56 % (2) 62% (3) 44% (4) 50%
[JEE Mains-2015]
Ans. (1)
Before collison
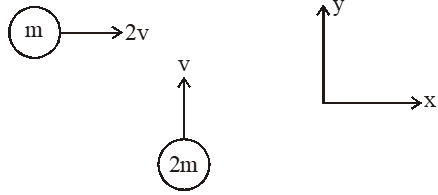 Kinetic energy $=\frac{1}{2} \mathrm{m}(2 \mathrm{v})^{2} \times \frac{1}{2} 2 \mathrm{m}(\mathrm{v})^{2}$
$=3 \mathrm{mv}^{2}$
After collison
Applying momentum conservation for inelastic collision
$2 \mathrm{mv} \hat{\mathrm{j}}+\mathrm{m} 2 \mathrm{v} \hat{\mathrm{i}}=3 \mathrm{m} \overrightarrow{\mathrm{v}}_{\mathrm{f}}$
$\left|\overrightarrow{\mathrm{v}}_{\mathrm{f}}\right|=\sqrt{\frac{8}{9}} \mathrm{v}$
$\mathrm{K}_{\mathrm{f}}=\frac{1}{2} \times 3 \mathrm{m} \times\left(\mathrm{v}_{\mathrm{f}}^{2}\right)=\frac{4 \mathrm{mv}^{2}}{3}$
$\% \Delta \mathrm{K}=\frac{\mathrm{K}_{1}-\mathrm{K}_{\mathrm{f}}}{\mathrm{K}_{\mathrm{i}}} \times 100=\frac{5 \mathrm{mv}^{2} / 3}{3 \mathrm{mv}^{2}} \times 100=\frac{5}{9} \times 100=56 \%$
Kinetic energy $=\frac{1}{2} \mathrm{m}(2 \mathrm{v})^{2} \times \frac{1}{2} 2 \mathrm{m}(\mathrm{v})^{2}$
$=3 \mathrm{mv}^{2}$
After collison
Applying momentum conservation for inelastic collision
$2 \mathrm{mv} \hat{\mathrm{j}}+\mathrm{m} 2 \mathrm{v} \hat{\mathrm{i}}=3 \mathrm{m} \overrightarrow{\mathrm{v}}_{\mathrm{f}}$
$\left|\overrightarrow{\mathrm{v}}_{\mathrm{f}}\right|=\sqrt{\frac{8}{9}} \mathrm{v}$
$\mathrm{K}_{\mathrm{f}}=\frac{1}{2} \times 3 \mathrm{m} \times\left(\mathrm{v}_{\mathrm{f}}^{2}\right)=\frac{4 \mathrm{mv}^{2}}{3}$
$\% \Delta \mathrm{K}=\frac{\mathrm{K}_{1}-\mathrm{K}_{\mathrm{f}}}{\mathrm{K}_{\mathrm{i}}} \times 100=\frac{5 \mathrm{mv}^{2} / 3}{3 \mathrm{mv}^{2}} \times 100=\frac{5}{9} \times 100=56 \%$
 Kinetic energy $=\frac{1}{2} \mathrm{m}(2 \mathrm{v})^{2} \times \frac{1}{2} 2 \mathrm{m}(\mathrm{v})^{2}$
$=3 \mathrm{mv}^{2}$
After collison
Applying momentum conservation for inelastic collision
$2 \mathrm{mv} \hat{\mathrm{j}}+\mathrm{m} 2 \mathrm{v} \hat{\mathrm{i}}=3 \mathrm{m} \overrightarrow{\mathrm{v}}_{\mathrm{f}}$
$\left|\overrightarrow{\mathrm{v}}_{\mathrm{f}}\right|=\sqrt{\frac{8}{9}} \mathrm{v}$
$\mathrm{K}_{\mathrm{f}}=\frac{1}{2} \times 3 \mathrm{m} \times\left(\mathrm{v}_{\mathrm{f}}^{2}\right)=\frac{4 \mathrm{mv}^{2}}{3}$
$\% \Delta \mathrm{K}=\frac{\mathrm{K}_{1}-\mathrm{K}_{\mathrm{f}}}{\mathrm{K}_{\mathrm{i}}} \times 100=\frac{5 \mathrm{mv}^{2} / 3}{3 \mathrm{mv}^{2}} \times 100=\frac{5}{9} \times 100=56 \%$
Kinetic energy $=\frac{1}{2} \mathrm{m}(2 \mathrm{v})^{2} \times \frac{1}{2} 2 \mathrm{m}(\mathrm{v})^{2}$
$=3 \mathrm{mv}^{2}$
After collison
Applying momentum conservation for inelastic collision
$2 \mathrm{mv} \hat{\mathrm{j}}+\mathrm{m} 2 \mathrm{v} \hat{\mathrm{i}}=3 \mathrm{m} \overrightarrow{\mathrm{v}}_{\mathrm{f}}$
$\left|\overrightarrow{\mathrm{v}}_{\mathrm{f}}\right|=\sqrt{\frac{8}{9}} \mathrm{v}$
$\mathrm{K}_{\mathrm{f}}=\frac{1}{2} \times 3 \mathrm{m} \times\left(\mathrm{v}_{\mathrm{f}}^{2}\right)=\frac{4 \mathrm{mv}^{2}}{3}$
$\% \Delta \mathrm{K}=\frac{\mathrm{K}_{1}-\mathrm{K}_{\mathrm{f}}}{\mathrm{K}_{\mathrm{i}}} \times 100=\frac{5 \mathrm{mv}^{2} / 3}{3 \mathrm{mv}^{2}} \times 100=\frac{5}{9} \times 100=56 \%$
Q. Distance of the centre of mass of a solid uniform cone from its vertex is $\mathrm{Z}_{0}$. If the radius of its base is R and its height is h then $\mathrm{Z}_{0}$ is equal to :-
(1) $\frac{5 \mathrm{h}}{8}$
(2) $\frac{3 \mathrm{h}^{2}}{8 \mathrm{R}}$
(3) $\frac{\mathrm{h}^{2}}{4 \mathrm{R}}$
(4) $\frac{3 \mathrm{h}}{4}$
[JEE Mains-2015]
Ans. (4)
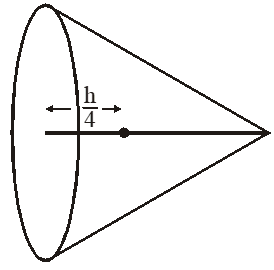 for solid cone c.m. is $\frac{\mathrm{h}}{4}$ from base
so $\mathrm{z}_{0}=\mathrm{h}-\frac{\mathrm{h}}{4}=\frac{3 \mathrm{h}}{4}$
for solid cone c.m. is $\frac{\mathrm{h}}{4}$ from base
so $\mathrm{z}_{0}=\mathrm{h}-\frac{\mathrm{h}}{4}=\frac{3 \mathrm{h}}{4}$
 for solid cone c.m. is $\frac{\mathrm{h}}{4}$ from base
so $\mathrm{z}_{0}=\mathrm{h}-\frac{\mathrm{h}}{4}=\frac{3 \mathrm{h}}{4}$
for solid cone c.m. is $\frac{\mathrm{h}}{4}$ from base
so $\mathrm{z}_{0}=\mathrm{h}-\frac{\mathrm{h}}{4}=\frac{3 \mathrm{h}}{4}$
Q. It is found that if a neutron suffers an elastic collinear collision with deuterium at rest, fractional loss of its energy is $\mathrm{P}_{\mathrm{d}}$ ; while for its similar collision with carbon nucleus at rest, fractional loss of energy is $\mathrm{P}_{\mathrm{c}}$. The values of $\mathrm{P}_{\mathrm{d}}$ and $\mathrm{P}_{\mathrm{c}}$ are respectively :
(1) (.28, .89)
(2) (0, 0)
(3) (0, 1)
(4) (.89, .28)
[JEE Mains-2018]
Ans. (4)
Let initial speed of neutron is $\mathrm{v}_{0}$ and kinetic energy is K.
1st collision :
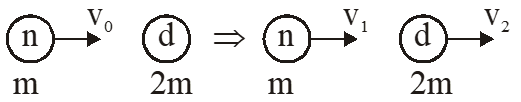 by momentum conservation
$\mathrm{mv}_{0}=\mathrm{mv}_{1}+2 \mathrm{mv}_{2} \Rightarrow \mathrm{v}_{1}+2 \mathrm{v}_{2}=\mathrm{v}_{0}$
by $\mathrm{e}=1 \quad \mathrm{v}_{2}-\mathrm{v}_{1}=\mathrm{v}_{0}$
by momentum conservation
$\mathrm{mv}_{0}=\mathrm{mv}_{1}+2 \mathrm{mv}_{2} \Rightarrow \mathrm{v}_{1}+2 \mathrm{v}_{2}=\mathrm{v}_{0}$
by $\mathrm{e}=1 \quad \mathrm{v}_{2}-\mathrm{v}_{1}=\mathrm{v}_{0}$
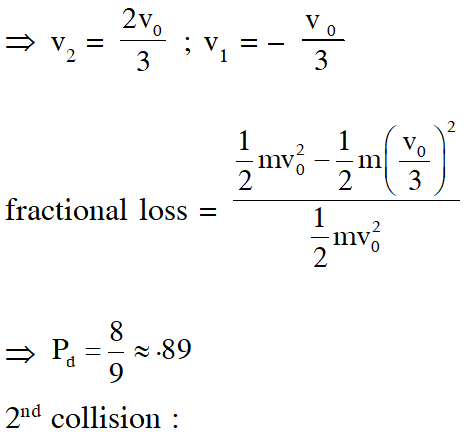
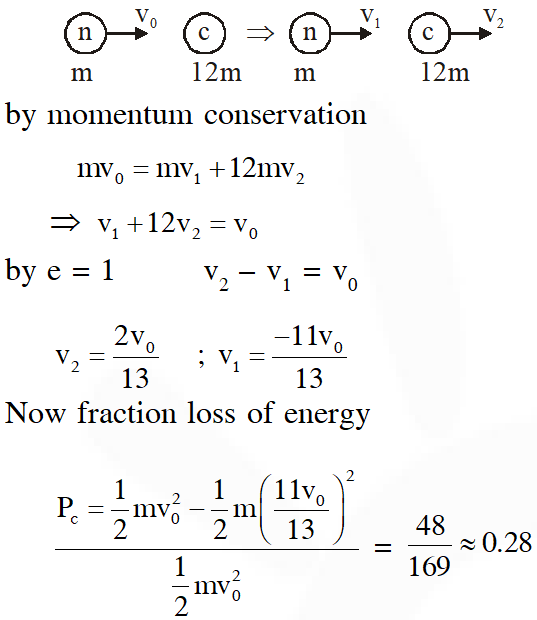
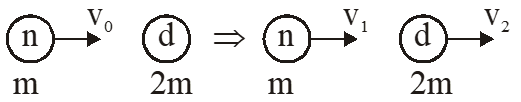 by momentum conservation
$\mathrm{mv}_{0}=\mathrm{mv}_{1}+2 \mathrm{mv}_{2} \Rightarrow \mathrm{v}_{1}+2 \mathrm{v}_{2}=\mathrm{v}_{0}$
by $\mathrm{e}=1 \quad \mathrm{v}_{2}-\mathrm{v}_{1}=\mathrm{v}_{0}$
by momentum conservation
$\mathrm{mv}_{0}=\mathrm{mv}_{1}+2 \mathrm{mv}_{2} \Rightarrow \mathrm{v}_{1}+2 \mathrm{v}_{2}=\mathrm{v}_{0}$
by $\mathrm{e}=1 \quad \mathrm{v}_{2}-\mathrm{v}_{1}=\mathrm{v}_{0}$
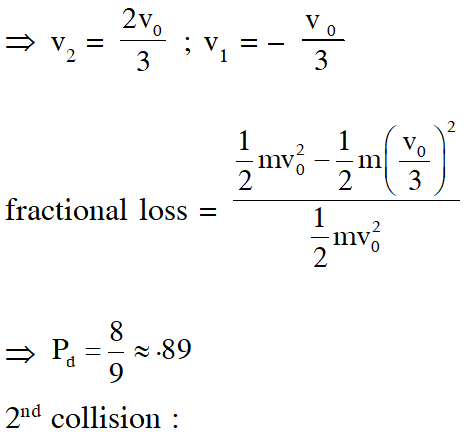
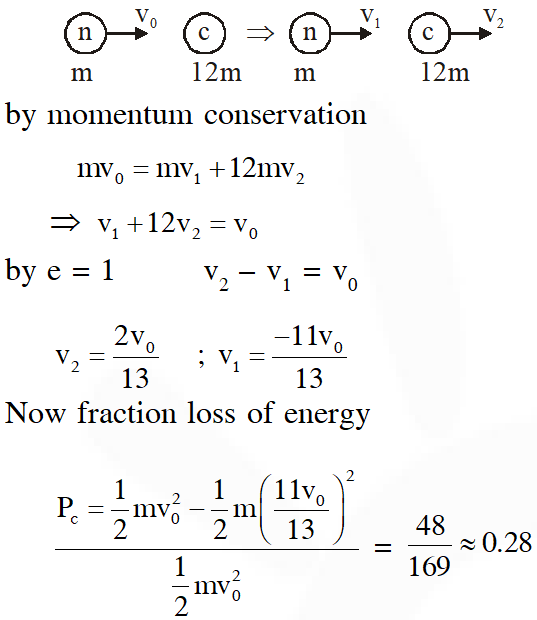
Q. In a collinear collision, a particle with an initial speed $\mathrm{V}_{0}$ strikes a stationary particle of the same mass. If the final total kinetic energy is 50% greater than the original kinetic energy, the magnitude of the relative velocity between the two particles, after collision, is :
(1) $\sqrt{2} \mathrm{v}_{0}$
(2)$\frac{\mathrm{v}_{0}}{2}$
(3) $\frac{\mathrm{v}_{0}}{\sqrt{2}}$
(4) $\frac{\mathrm{v}_{0}}{4}$
[JEE Mains-2018]
Ans. (1)
Initial
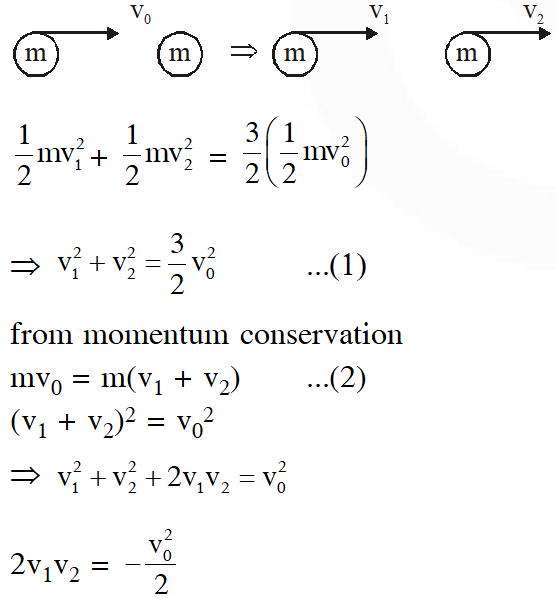
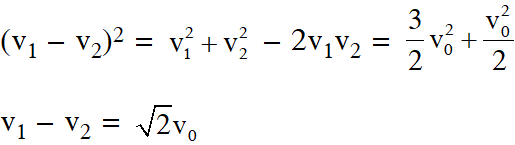
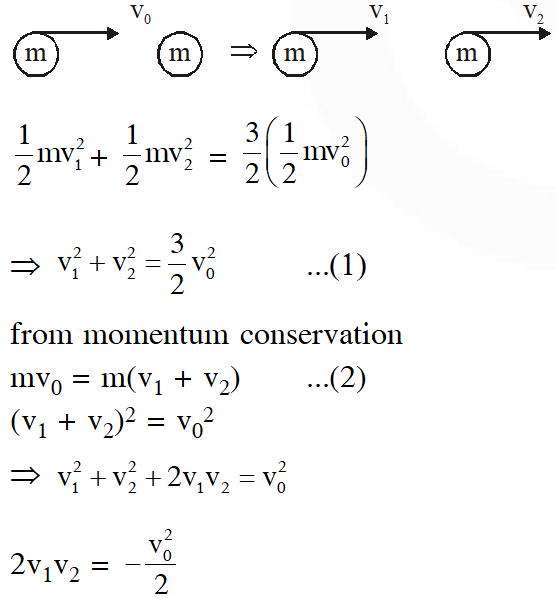
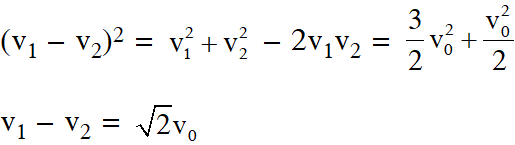
Comments
bibhudatta behera
Aug. 31, 2020, 12:46 p.m.
whose has not mind to study he says that esaral is worst.it is the best platform to everybody.
