JEE Advanced Previous Year Questions of Math with Solutions are available at eSaral. Practicing JEE Advanced Previous Year Papers Questions of mathematics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral also provides complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Let $\mathrm{S}=\mathrm{S}_{1} \cap \mathrm{S}_{2} \cap \mathrm{S}_{3},$ where $\mathrm{S}_{1}=\{\mathrm{z} \in \mathrm{C}:|\mathrm{z}|<4\}, \mathrm{S}_{2}=\left\{\mathrm{z} \in \mathrm{C}: \operatorname{Im}\left[\frac{\mathrm{z}-1+\sqrt{3} \mathrm{i}}{1-\sqrt{3} \mathrm{i}}\right]>0\right\}$ and $\mathrm{S}_{3}=\{\mathrm{z} \in \mathrm{C}: \operatorname{Re} \mathrm{z}>0\}$
Q. Let $\mathrm{z}=\cos \theta+\mathrm{i} \sin \theta .$ Then the value of $\sum_{\mathrm{m}=1}^{15} \operatorname{Im}\left(\mathrm{z}^{2 \mathrm{m}-1}\right)$ at $\theta=2^{\circ}$ is
(A) $\frac{1}{\sin 2^{\circ}}$
(B) $\frac{1}{3 \sin 2^{\circ}}$
(C) $\frac{1}{2 \sin 2^{\circ}}$
(D) $\frac{1}{4 \sin 2^{\circ}}$
[JEE 2009, 3M,-1M]
Ans. (D)
$\mathrm{z}=\cos \theta+\mathrm{i} \sin \theta=\mathrm{e}^{\mathrm{i} \theta}$
$\therefore \sum_{m=1}^{15} \operatorname{Im}\left(z^{2 m-1}\right)=\sum_{m=1}^{15} \operatorname{Im}\left(e^{i \theta}\right)^{2 m-1}=\sum_{m=1}^{15} \operatorname{Im} e^{i(2 m-1) \theta}$
$=\sin \theta+\sin 3 \theta+\ldots \ldots+\sin 29 \theta$
$=\frac{\sin \left(\frac{\theta+29 \theta}{2}\right) \cdot \sin \left(\frac{15 \times 2 \theta}{2}\right)}{\sin \frac{2 \theta}{2}}$c
$=\frac{\sin (15 \theta) \cdot \sin (15 \theta)}{\sin \theta}, \theta=2^{\circ}$b
$=\frac{1}{4 \sin 2^{\circ}}$
Q. Let $z=x+$ iy be a complex number where $x$ and $y$ are integers. Then the area of the rectangle whose vertices are the roots of the equation $z \bar{z}^{3}+\bar{z} z^{3}=350$ is
(A) 48 (B) 32 (C) 40 (D) 80
[JEE 2009, 3 + 3]
Ans. (A)
$z \bar{z}\left(z^{2}+z^{-2}\right)=350$
$2\left(x^{2}+y^{2}\right)\left(x^{2}-y^{2}\right)=350$
$\left(x^{2}+y^{2}\right)\left(x^{2}-y^{2}\right)=175$
$\because \mathrm{x}, \mathrm{y} \in \mathrm{I}$ the only possible case which gives integral solutions
$\mathrm{x}^{2}+\mathrm{y}^{2}=25$
$\mathrm{x}^{2}-\mathrm{y}^{2}=7$
$\mathrm{x}^{2}=16, \mathrm{y}^{2}=9$
$\mathrm{x}=\pm 4, \mathrm{y}=\pm 3$
Area of rectangle $=8 \times 6=48$
Q. Let $z_{1}$ and $z_{2}$ be two distinct complex numbers and let $z=(1-t) z_{1}+t z_{2}$ for some real number $t$ with $0
(A) $\left|z-z_{1}\right|+\left|z-z_{2}\right|=\left|z_{1}-z_{2}\right|$
(B) $\operatorname{Arg}\left(\mathrm{z}-\mathrm{z}_{1}\right)=\operatorname{Arg}\left(\mathrm{z}-\mathrm{z}_{2}\right)$
(C) $\left|\begin{array}{cc}{\mathrm{z}-\mathrm{z}_{1}} & {\overline{\mathrm{z}}-\overline{\mathrm{z}}_{1}} \\ {\mathrm{z}_{2}-\mathrm{z}_{1}} & {\overline{\mathrm{z}}_{2}-\overline{\mathrm{z}}_{1}}\end{array}\right|=0$
(D) $\operatorname{Arg}\left(\mathrm{z}-\mathrm{z}_{1}\right)=\operatorname{Arg}\left(\mathrm{z}_{2}-\mathrm{z}_{1}\right)$
[JEE 2009, 3 + 3]
Ans. (A,C,D)
$\mathrm{z}=\mathrm{z}_{1}+\mathrm{t}\left(\mathrm{z}_{2}-\mathrm{z}_{1}\right)$
$\frac{\mathrm{z}-\mathrm{z}_{1}}{\mathrm{z}_{2}-\mathrm{z}_{1}}=\mathrm{t}, \mathrm{t} \in(0,1)$
$\Rightarrow \mathrm{z}=\frac{\mathrm{z}_{1}(1-\mathrm{t})+\mathrm{t} z_{2}}{(1+\mathrm{t})+\mathrm{t}}$
point $\mathrm{P}(\mathrm{z})$ divides point $\mathrm{A}\left(\mathrm{z}_{1}\right) \& \mathrm{B}\left(\mathrm{z}_{2}\right)$ internally in ratio $(1-\mathrm{t}): \mathrm{t}$
Hence locus is a line segment such that $\mathrm{P}(\mathrm{z})$ lies between $\mathrm{A}\left(\mathrm{z}_{1}\right) \& \mathrm{B}\left(\mathrm{z}_{2}\right)$ as shown in figure.
Hence options A,C & D are correct.
Hence options A,C & D are correct.
Q. Let $\omega$ be the complex number $\cos \frac{2 \pi}{3}+$ isin $\frac{2 \pi}{3} .$ Then the number of distinct complex numbers $z$ satisfying $\left|\begin{array}{ccc}{\mathrm{z}+1} & {\omega} & {\omega^{2}} \\ {\omega} & {\mathrm{z}+\omega^{2}} & {1} \\ {\omega^{2}} & {1} & {\mathrm{z}+\omega}\end{array}\right|=0$ is equal to
Ans. 1
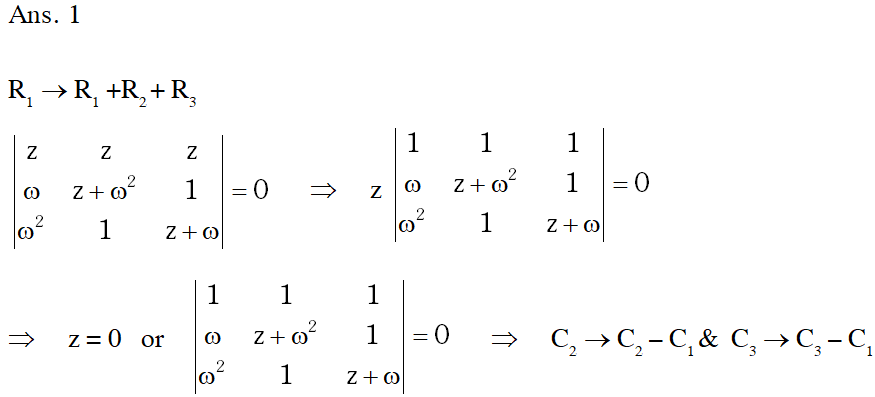
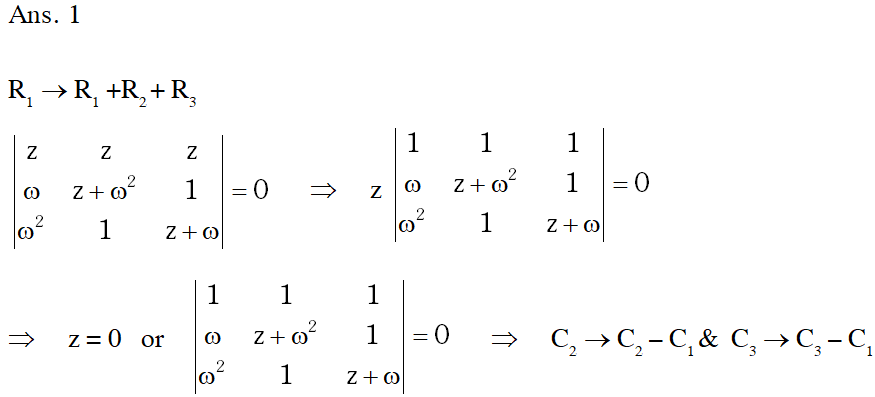
Q. Match the statements in Column-I with those in Column II.
[Note : Here z takes values in the complex plane and Im z and Re z denote, respectively, the imaginary part and the real part of z.]
[JEE 10, 3+3+8]
[JEE 10, 3+3+8]
Ans. ((A) Q,R (B) P (C) P,S,T (D) Q,R,S,T )
(A) $\left.|z-i| z\right|^{2}=|z+i| z||^{2}$
$\quad \Rightarrow(z-i|z|)(\bar{z}+i|z|)=(z+i|z|)(\bar{z}-i|z|)$
$\quad \Rightarrow 2 i|z| z=2 i|z| \bar{z}$
$\quad \Rightarrow z=\bar{z} \quad \therefore z$ is purely real.
$\quad \therefore z$ lies on real axis.
(B) Locus is ellipse having focii $(-4,0) \&(4,0)$
2ae $=8$ \& $2 \mathrm{a}=10$
$\Rightarrow \mathrm{a}=5 \quad \& \quad \mathrm{e}=4 / 5$
It is ellipse having eccentricity $4 / 5$.
(C) $\mathrm{w}=2(\cos \theta+\mathrm{i} \sin \theta)$
$\quad \mathrm{z}=2(\cos \theta+\mathrm{i} \sin \theta)-\frac{1}{2(\cos \theta+\mathrm{i} \sin \theta)}$
$\quad \mathrm{x}+\mathrm{iy}=\frac{3}{2} \cos \theta+\frac{\mathrm{i} 5}{2} \sin \theta$
$\quad \Rightarrow \quad \mathrm{x}=\frac{3}{2} \cos \theta \quad \& \quad \mathrm{y}=\frac{5}{2} \sin \theta$
It is a locus $\frac{x^{2}}{9 / 4}+\frac{y^{2}}{25 / 4}=1$
$\frac{9}{4}=\frac{25}{4}\left(1-e^{2}\right) \Rightarrow e=\frac{4}{5}$
since $\mathrm{x}=\frac{3}{2} \cos \theta \quad \Rightarrow \quad|\operatorname{Re}(z)| \leq \frac{3}{2}$
$|\operatorname{Re}(z)| \leq \frac{3}{2} \quad \Rightarrow \quad|\operatorname{Re}(z)| \leq 2$
Consider the circle $\mathrm{x}^{2}+\mathrm{y}^{2}-9=0$
By putting $\mathrm{x}=\frac{3}{2} \cos \theta$
$\& y=\frac{5}{2} \sin \theta$ into $x^{2}+y^{2}-9$
$\frac{9 \cos ^{2} \theta}{4}+\frac{25}{4} \sin ^{2} \theta-9<0$
(D) $z=(\cos \theta+i \sin \theta)+\frac{1}{(\cos \theta+i \sin \theta)}$
$z=2 \cos \theta$
where $z$ is real value $\& z \in[-2,2]$z
Q. Comprehension (3 questions together)
Let a,b and c be three real numbers satisfying
(i) If the point P(a,b,c), with reference to (E), lies on the plane 2x + y + z = 1, then the
value of 7a+b+c is
(A) 0 (B) 12 (C) 7 (D) 6
(ii) Let be a solution of $x^{3}-1=0$ with Im() > 0. If a = 2 with b and c satisfying (E), then the value of $\frac{3}{\omega^{a}}+\frac{1}{\omega^{b}}+\frac{3}{\omega^{c}}$ is equal to –
(A) –2 (B) 2 (C) 3 (D) –3
(iii) Let b = 6, with a and c satisfying (E). If $\alpha$ and $\beta$ are the roots of the quadratic equation $\mathrm{ax}^{2}+\mathrm{bx}+\mathrm{c}=0,$ then $\sum_{\mathrm{n}=0}^{\infty}\left(\frac{1}{\alpha}+\frac{1}{\beta}\right)^{\mathrm{n}}$ is –
(A) 6 (B) 7 (C) $\frac{6}{7}$ $(D) \infty$
[JEE 2011, 3+3+3]
(i) If the point P(a,b,c), with reference to (E), lies on the plane 2x + y + z = 1, then the
value of 7a+b+c is
(A) 0 (B) 12 (C) 7 (D) 6
(ii) Let be a solution of $x^{3}-1=0$ with Im() > 0. If a = 2 with b and c satisfying (E), then the value of $\frac{3}{\omega^{a}}+\frac{1}{\omega^{b}}+\frac{3}{\omega^{c}}$ is equal to –
(A) –2 (B) 2 (C) 3 (D) –3
(iii) Let b = 6, with a and c satisfying (E). If $\alpha$ and $\beta$ are the roots of the quadratic equation $\mathrm{ax}^{2}+\mathrm{bx}+\mathrm{c}=0,$ then $\sum_{\mathrm{n}=0}^{\infty}\left(\frac{1}{\alpha}+\frac{1}{\beta}\right)^{\mathrm{n}}$ is –
(A) 6 (B) 7 (C) $\frac{6}{7}$ $(D) \infty$
[JEE 2011, 3+3+3]
Ans. ((i) $\mathrm{D} \quad$ (ii) $\mathrm{A} \quad$ (iii) $\mathrm{B}$)
Comprehension $(3$ questions together)
$\mathrm{a}+8 \mathrm{b}+7 \mathrm{c}=0$
$9 \mathrm{a}+2 \mathrm{b}+3 \mathrm{c}=0$
$7 \mathrm{a}+7 \mathrm{b}+7 \mathrm{c}=0$
$\Rightarrow \quad \mathrm{a}=\mathrm{K}, \mathrm{b}=6 \mathrm{K}, \mathrm{c}=-7 \mathrm{K}$
$\quad(\mathrm{K}, 6 \mathrm{K},-7 \mathrm{K})$
$2 \mathrm{x}+\mathrm{y}+\mathrm{z}=1$
$2 \mathrm{K}+6 \mathrm{K}-7 \mathrm{K}=1$
$\begin{aligned} &(\because \text { point lies on the plane }) \\ \Rightarrow & \mathrm{K}=1 \\ \Rightarrow & 7 \mathrm{a}+\mathrm{b}+\mathrm{c}=7 \mathrm{K}+6 \mathrm{K}-7 \mathrm{K}=6 \end{aligned}$
(ii) $x^{3}-1=0$
$\quad \Rightarrow x=1, \omega, \omega^{2}$
$\quad \omega=-\frac{1}{2}+\frac{i \sqrt{3}}{2}$
If $\quad a=2=K$
$\Rightarrow \quad b=12 \quad \& c=-14$
Hence $\frac{3}{\omega^{a}}+\frac{1}{\omega^{b}}+\frac{3}{\omega^{c}}=\frac{3}{\omega^{2}}+\frac{1}{\omega^{12}}+\frac{3}{\omega^{-14}}$
$=3 \omega+1+3 \omega^{2}=-3+1=-2$
$\begin{aligned}( \text { iii) } & \because \mathrm{b}=6 \quad \Rightarrow \quad 6 \mathrm{K}=6 \\ \Rightarrow & \mathrm{K}=1 \\ \Rightarrow & \mathrm{a}=1, \quad \mathrm{b}=6 \quad \& \quad \mathrm{c}=-7 \\ & \mathrm{x}^{2}+6 \mathrm{x}-7=0 \\ & \Rightarrow \alpha+\beta=-6, \alpha \beta=-7 \\ & \Rightarrow \quad \sum_{n=0}^{\infty}\left(\frac{\alpha+\beta}{\alpha \beta}\right)^{n}=\sum_{n=0}^{\infty}\left(\frac{6}{7}\right)^{n}=\frac{1}{1-\frac{6}{7}}=7 \end{aligned}$
Q. If $z$ is any complex number satisfying $|z-3-2 i| \leq 2,$ then the minimum value of $|2 z-6+5 i|$ is
[JEE 2011, 4M]
Ans. 5
We have to find minimum value of
$$
2\left|z-\left(3-\frac{5}{2} i\right)\right|
$$
$=2 \times$ (minimum distance between $\mathrm{z}$ and point
$\left.\qquad\left(3,-\frac{5}{2}\right)\right)$
$=2 \times\left(\text { distance between }(3,0) \text { and }\left(3,-\frac{5}{2}\right)\right)$
$=2 \times \frac{5}{2}=5$ units.
We have to find minimum value of
$$
2\left|z-\left(3-\frac{5}{2} i\right)\right|
$$
$=2 \times$ (minimum distance between $\mathrm{z}$ and point
$\left.\qquad\left(3,-\frac{5}{2}\right)\right)$
$=2 \times\left(\text { distance between }(3,0) \text { and }\left(3,-\frac{5}{2}\right)\right)$
$=2 \times \frac{5}{2}=5$ units.
Q. Let $\omega=\mathrm{e}^{\mathrm{i} \pi / 3},$ and $\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{x}, \mathrm{y}, \mathrm{z}$ be non-zero complex numbers such that
$a+b+c=x$
$a+b \omega+c \omega^{2}=y$
$a+b \omega^{2}+c \omega=z$
Then the value of $\frac{|\mathrm{x}|^{2}+|\mathrm{y}|^{2}+|\mathrm{z}|^{2}}{|\mathrm{a}|^{2}+|\mathrm{b}|^{2}+|\mathrm{c}|^{2}}$ is
[JEE 2011, 4M]
Ans. (Bonus)
Ans. 3 (Bonus)
(Comment : If $\omega=\mathrm{e}^{\mathrm{i} \pi / 3}$
then $\frac{|x|^{2}+|y|^{2}+|z|^{2}}{|a|^{2}+|b|^{2}+|c|^{2}}$ is not always an integer.
For example if $a=b=c=1$ then the value of $\frac{|x|^{2}+|y|^{2}+|z|^{2}}{|a|^{2}+|b|^{2}+|c|^{2}}$. Now if we consider
$\omega=\mathrm{e}^{\mathrm{i} 2 \pi / 3}$ then the solution is
$|\mathrm{x}|^{2}=(\mathrm{a}+\mathrm{b}+\mathrm{c})(\overline{\mathrm{a}}+\overline{\mathrm{b}}+\overline{\mathrm{c}})$
$=|\mathrm{a}|^{2}+\left.|\mathrm{b} \hat{\mathrm{p}}+| \mathrm{c}\right|^{2}+\mathrm{a} \overline{\mathrm{b}}+\overline{\mathrm{a} \overline{\mathrm{c}}}+\overline{\mathrm{b} \overline{\mathrm{a}}}+\mathrm{b} \overline{\mathrm{c}}+\mathrm{c} \overline{\mathrm{a}}+\mathrm{c} \overline{\mathrm{b}}$
$|\mathrm{y}|^{2}=\left(\mathrm{a}+\mathrm{b} \omega+\mathrm{c} \omega^{2}\right)\left(\overline{\mathrm{a}}+\overline{\mathrm{b}} \omega^{2}+\overline{\mathrm{c}} \omega\right)$
$=|a|^{2}+|b|^{2}+|c|^{2}+a \bar{b} \omega^{2}+a \bar{c} \omega+b \bar{a} \omega+b \bar{c} \omega^{2}+c \bar{a} \omega^{2}+c \bar{b} \omega$
$|z|^{2}=\left(a+b \omega^{2}+c \omega\right)\left(\bar{a}+\bar{b} \omega+\bar{c} \omega^{2}\right)$
$=|a|^{2}+|b|^{2}+\left|c^{2}\right|$
$+a \bar{b} \omega+a \bar{c} \omega^{2}+b \bar{a} \omega^{2}+b \bar{c} \omega+c \bar{a} \omega+c \bar{b} \omega^{2}$
$\therefore|x|^{2}+|y|^{2}+|z|^{2}=3\left(|a|^{2}+|b|^{2}+|c|^{2}\right)$
$\Rightarrow \frac{|x|^{2}+|y|^{2}+|z|^{2}}{|a|^{2}+|b|^{2}+|c|^{2}}=3$
Q. Match the statements given in Column I with the values given in Column II
[JEE 2011, 2+2+2+2M]
[JEE 2011, 2+2+2+2M]
Ans. ( (A) q (B) p or p,q,r,s,t (C) s (D) t )
Q. Match the statements given in Column I with the intervals/union of intervals given in Column II
[JEE 2011, 2+2+2+2M]
[JEE 2011, 2+2+2+2M]
Ans. ($\begin{array}{llll}{\text { (A) } s} & {\text { (B) } t} & {\text { (C) } r} & {\text { (D) } r}\end{array}$)
(A) Let $z=\cos \theta+i \sin \theta$
$\quad \operatorname{Re}\left(\frac{2 i(\cos \theta+i \sin \theta)}{1-(\cos \theta+i \sin \theta)^{2}}\right)=\operatorname{Re}\left(\frac{i \cos \theta-\sin \theta}{\sin ^{2} \theta-i \cos \theta \sin \theta}\right)$
$=\operatorname{Re}\left(-\frac{1}{\sin \theta}\right)=\frac{-1}{\sin \theta}$
$\begin{aligned} \therefore & \text { Set will be }(-\infty,-1] \cup[1, \infty) \\-1 \leq & \frac{8.3^{(x-2)}}{1-3^{2(x-1)}} \leq 1 \quad \mathrm{x} \neq 1 \\ \Rightarrow &-1 \leq \frac{8.3^{x}}{\left(3-3^{x}\right)\left(3+3^{x}\right)} \leq 1 \end{aligned}$
$3^{\mathrm{x}}=\mathrm{t} \quad \therefore \quad \mathrm{t}>0$
$\frac{8 \mathrm{t}}{(3-\mathrm{t})(\mathrm{t}+3)} \geq-1$
$\Rightarrow \quad \mathrm{t} \in(0,3) \cup[9, \infty)$
$\Rightarrow \quad x \in(-\infty, 1) \cup[2, \infty)$
$\quad \frac{8 t}{(3-t)(t+3)} \leq 1$
$\quad \Rightarrow \quad t \in(0,1] \cup(3, \infty)$
$\quad \Rightarrow \quad x \in(-\infty, 0] \cup(1, \infty)$
Taking intersection
$x \in(-\infty, 0] \cup[2, \infty)$
(D) $f(x)=3 x^{5 / 2}-10 x^{3 / 2}$
$f^{\prime}(x)=\frac{15}{2} x^{3 / 2}-\frac{30}{2} x^{1 / 2}>0$
$\Rightarrow \frac{15}{2} \sqrt{x}(x-2) \geq 0 \quad \Rightarrow \quad x \geq 2$
(D) $f(x)=3 x^{5 / 2}-10 x^{3 / 2}$
$f^{\prime}(x)=\frac{15}{2} x^{3 / 2}-\frac{30}{2} x^{1 / 2}>0$
$\Rightarrow \frac{15}{2} \sqrt{x}(x-2) \geq 0 \quad \Rightarrow \quad x \geq 2$
Q. Let z be a complex number such that the imaginary part of $z$ is nonzero and a $=z^{2}+z+1$ is real. Then a cannot take the value $-$
(A) –1
(B) $\frac{1}{3}$
(C) $\frac{1}{2}$
(D) $\frac{3}{4}$
[JEE 2012, 3M, –1M]
Ans. (D)
$\mathrm{z}^{2}+\mathrm{z}+1-\mathrm{a}=0$
$\because \mathrm{z}$ is imaginary $\Rightarrow \mathrm{D}<0$
$1-4(1-\mathrm{a})<0$
$4 \mathrm{a}<3$
$\mathrm{a}<\frac{3}{4}$
Aliter $: a=z^{2}+z+1$
$\because \quad a=\bar{a}(\text { given a is real })$
$\therefore \quad z^{2}+z=\bar{z}^{2}+$
$\Rightarrow \quad z^{2}-\bar{z}^{2}=\bar{z}-z$
$\Rightarrow \quad z+\bar{z}=-1 \quad(\because \operatorname{Im}(z) \text { is non zero })$
$\Rightarrow \quad \operatorname{Re}(\mathrm{z})=-\frac{1}{2}$
$\therefore \quad \mathrm{z}$ can be taken as $-\frac{1}{2}+\mathrm{iy}$
where $\mathrm{y} \in \mathrm{R}$
$\therefore \quad \mathrm{a}=\left(-\frac{1}{2}+\mathrm{i} y\right)^{2}+\left(\frac{-1}{2}+\mathrm{iy}\right)+1$
$\Rightarrow \quad \mathrm{a}=\frac{1}{4}-\frac{1}{2}+1-\mathrm{i} y+\mathrm{i} y-\mathrm{y}^{2}$
$\Rightarrow \quad a=\frac{3}{4}-y^{2} \Rightarrow a<\frac{3}{4}$
$\therefore \quad a \neq \frac{3}{4}$
Q. Let complex numbers $\alpha$ and $\frac{1}{\bar{\alpha}}$ lie on circles $\left(\mathrm{x}-\mathrm{x}_{0}\right)^{2}+\left(\mathrm{y}-\mathrm{y}_{0}\right)^{2}=\mathrm{r}^{2}$ and $\left(\mathrm{x}-\mathrm{x}_{0}\right)^{2}+\left(\mathrm{y}-\mathrm{y}_{0}\right)^{2}=$
$4 \mathrm{r}^{2}$ respectively. If $\mathrm{z}_{0}=\mathrm{x}_{0}+\mathrm{iy}_{0}$ satisfies the equation $2\left|\mathrm{z}_{0}\right|^{2}=\mathrm{r}^{2}+2,$ then $|\alpha|=$
(A) $\frac{1}{\sqrt{2}}$
(B) $\frac{1}{2}$
(C) $\frac{1}{\sqrt{7}}$
(D) $\frac{1}{3}$
[JEE(Advanced) 2013, 2M]
Ans. (C)
Q. Let $\omega$ be a complex cube root of unity with $\omega \neq 1$ and $\mathrm{P}=\left[\mathrm{p}_{\mathrm{ij}}\right]$ be a $\mathrm{n} \times \mathrm{n}$ matrix with $\mathrm{p}_{\mathrm{ij}}=$ $\omega^{\mathrm{i}+\mathrm{j}} .$ Then $\mathrm{P}^{2} \neq 0,$ when $\mathrm{n}=$
(A) 57 (B) 55 (C) 58 (D) 56
[JEE(Advanced) 2013, 3, (–1)]
Ans. (B,C,D)
$\mathrm{P}^{2}=\left[\alpha_{\mathrm{ij}}\right]_{\mathrm{n} \times \mathrm{n}}$
$\alpha_{\mathrm{ij}}=\sum_{\mathrm{k}=1}^{\mathrm{n}} \mathrm{p}_{\mathrm{ik}} \cdot \mathrm{P}_{\mathrm{kj}}$
$=\sum_{\mathrm{k}=1}^{\mathrm{n}} \omega^{\mathrm{i}+\mathrm{k}} \cdot \omega^{\mathrm{k}+\mathrm{j}}=\omega^{\mathrm{i}+\mathrm{j}} \sum_{\mathrm{k}=1}^{\mathrm{n}} \omega^{2 \mathrm{k}}$
$=\omega^{\mathrm{i}+\mathrm{j}}\left(\omega^{2}+\omega^{4}+\omega^{6}+\ldots \ldots+\omega^{2 \mathrm{n}}\right)$
If $\mathrm{n}$ is a multiple of 3 then $\mathrm{P}^{2}=0$
$\Rightarrow \mathrm{n}$ is not a multiple of 3
$\Rightarrow \mathrm{n}$ can be $55,58,56$
Q. Let $\mathrm{w}=\frac{\sqrt{3}+\mathrm{i}}{2}$ and $\mathrm{P}=\left\{\mathrm{w}^{\mathrm{n}}: \mathrm{n}=1,2,3, \ldots . .\right\} .$ Further $\mathrm{H}_{1}=\left\{\mathrm{z} \in \mathrm{C}: \operatorname{Re} \mathrm{z}>\frac{1}{2}\right\}$ and $\mathrm{H}_{2}=\left\{\mathrm{z} \in \mathrm{C}: \operatorname{Re} \mathrm{z}<\frac{-1}{2}\right\},$ where $\mathrm{C}$ is the set of all complex numbers. If $\mathrm{z}_{1} \in \mathrm{P} \cap \mathrm{H}_{1}, \mathrm{z}_{2} \in \mathrm{P}$ $\cap \mathrm{H}_{2}$ and $\mathrm{O}$ represents the origin, then $\angle \mathrm{z}_{1} \mathrm{O} \mathrm{z}_{2}=$
(A) $\frac{\pi}{2}$
(B) $\frac{\pi}{6}$
(C) $\frac{2 \pi}{3}$
(D) $\frac{5 \pi}{6}$
[JEE-Advanced 2013, 4, (–1)]
Ans. (C,D)
$\mathrm{z}_{1}=\left\{\mathrm{w}_{1}, \mathrm{w}_{11}, \mathrm{w}_{12}\right\}$
$\mathrm{z}_{2}=\left\{\mathrm{w}_{5}, \mathrm{w}_{6}, \mathrm{w}_{7}\right\}$
$\angle \mathrm{w}_{1} \mathrm{O} \mathrm{w}_{5}=\frac{2 \pi}{3} \& \angle \mathrm{w}_{1} \mathrm{O} \mathrm{w}_{6}=\frac{5 \pi}{6}$
$\mathrm{z}_{1}=\left\{\mathrm{w}_{1}, \mathrm{w}_{11}, \mathrm{w}_{12}\right\}$
$\mathrm{z}_{2}=\left\{\mathrm{w}_{5}, \mathrm{w}_{6}, \mathrm{w}_{7}\right\}$
$\angle \mathrm{w}_{1} \mathrm{O} \mathrm{w}_{5}=\frac{2 \pi}{3} \& \angle \mathrm{w}_{1} \mathrm{O} \mathrm{w}_{6}=\frac{5 \pi}{6}$
Q. $\min _{\mathbf{z} \in \mathrm{S}}|1-3 \mathbf{i}-\mathbf{z}|=$
(A) $\frac{2-\sqrt{3}}{2}$
(B) $\frac{2+\sqrt{3}}{2}$
(C) $\frac{3-\sqrt{3}}{2}$
(D) $\frac{3+\sqrt{3}}{2}$
[JEE(Advanced) 2013, 3, (–1)]
Ans. (C)
$\mathrm{S}_{1}$ is interior of circle centred at $(0,0) \&$ radius $=4$
$\operatorname{Re}(\mathrm{z})>0$ is in $\mathrm{I}^{\mathrm{st}} \& \mathrm{IV}^{\mathrm{th}} \mathrm{quadrant.}$
$\frac{(z-(1-i \sqrt{3}))}{(1-i \sqrt{3})}=\frac{((x-1)+i(y-\sqrt{3}))}{(1-i \sqrt{3})}$
$=\frac{((x-1)+i(y-\sqrt{3}))(1+i \sqrt{3})}{2}$
$\mathrm{I}_{\mathrm{m}}\left(\mathrm{S}_{2}\right)=\sqrt{3} \mathrm{x}+\mathrm{y}>0$
erpendicular distance from $(1,-3)$ to the line is $\mathrm{P}=\frac{\sqrt{3}-3}{2} |=\left(\frac{3-\sqrt{3}}{2}\right)$
$\operatorname{Re}(\mathrm{z})>0$ is in $\mathrm{I}^{\mathrm{st}} \& \mathrm{IV}^{\mathrm{th}} \mathrm{quadrant.}$
$\frac{(z-(1-i \sqrt{3}))}{(1-i \sqrt{3})}=\frac{((x-1)+i(y-\sqrt{3}))}{(1-i \sqrt{3})}$
$=\frac{((x-1)+i(y-\sqrt{3}))(1+i \sqrt{3})}{2}$
$\mathrm{I}_{\mathrm{m}}\left(\mathrm{S}_{2}\right)=\sqrt{3} \mathrm{x}+\mathrm{y}>0$
erpendicular distance from $(1,-3)$ to the line is $\mathrm{P}=\frac{\sqrt{3}-3}{2} |=\left(\frac{3-\sqrt{3}}{2}\right)$
Q. Area of S =
(A) $\frac{10 \pi}{3}$
(B) $\frac{20 \pi}{3}$
(C) $\frac{16 \pi}{3}$
(D) $\frac{32 \pi}{3}$
[JEE(Advanced) 2013, 3, (–1)]
Ans. (B)
Area of $\mathrm{S}=\frac{\pi(4)^{2}}{4}+\frac{1}{2}(4)^{2} \frac{\pi}{3}$
$\frac{8 \pi}{3}+4 \pi=\frac{20 \pi}{3}$
Q. The quadratic equation p(x) = 0 with real coefficients has purely imaginary roots. Then the equation p(p(x)) = 0 has
(A) only purely imaginary roots
(B) all real roots
(C) two real and two purely imaginary roots
(D) neither real nor purely imaginary roots.
[JEE(Advanced) 2014, 3(–1)]
Ans. (D)
Let $\mathrm{p}(\mathrm{x})=\mathrm{ax}^{2}+\mathrm{b}+\mathrm{c}$
$\mathrm{p}(\mathrm{x})=0 \Rightarrow \mathrm{x}=\frac{-\mathrm{b}+\sqrt{\mathrm{b}^{2}-4 \mathrm{ac}}}{2 \mathrm{a}}$
so $\mathrm{b}=0$ as roots are purely imaginary
so equation will be $\mathrm{ax}^{2}+\mathrm{c}=0\{\text { where 'a' and 'c' have same sign }\}$
Now $\mathrm{p}(\mathrm{p}(\mathrm{x}))=0$
$\Rightarrow \quad a p^{2}(x)+c=0 \quad \Rightarrow \quad p(x)=\pm \sqrt{-\frac{c}{a}}$
$a x^{2}+c=\pm \sqrt{-\frac{c}{a}} \quad \Rightarrow \quad x \notin R$
$\begin{aligned} \text { if } \mathrm{x} &=\mathrm{i} \beta \text { then } \\ &-\mathrm{a} \beta^{2}+\mathrm{c}=\pm \sqrt{-\frac{\mathrm{c}}{\mathrm{a}}} \quad \text { not possible } \end{aligned}$
(real) (imaginary)
So neither real nor purely imaginary roots.
Q. Let $\mathrm{z}_{\mathrm{k}}=\cos \left(\frac{2 \mathrm{k} \pi}{10}\right)+\mathrm{i} \sin \left(\frac{2 \mathrm{k} \pi}{10}\right) ; \mathrm{k}=1,2, \ldots \ldots 9$
[JEE(Advanced) 2014, 3(–1)]
[JEE(Advanced) 2014, 3(–1)]
Ans. (C)
(P) $\quad e^{\frac{i 2 k \pi}{10}} \cdot e^{\frac{i 2 \pi}{10}}=1 \quad \Rightarrow e^{i \frac{\pi}{10} x 2(k+1)}=1$
$\frac{\pi}{10}(2(\mathrm{k}+\mathrm{j}))=2 \mathrm{n} \pi$b
$(\mathrm{k}+\mathrm{j})=10$
Possible
(Q) $\quad e^{\frac{\mathrm{i} 2 \pi}{10}} \cdot z=\mathrm{e}^{\frac{\mathrm{i} 2 \pi \mathrm{k}}{10}}$ $$
\mathrm{z}=\frac{\mathrm{e}^{\frac{\mathrm{i} 2 \pi \mathrm{k}}{10}}}{\frac{\mathrm{i} 2 \pi}{10}} \text { is possible } $$
(R) $\quad \mathrm{z}^{10}-1=(\mathrm{z}-1)\left(\mathrm{z}-\mathrm{z}_{1}\right)\left(\mathrm{z}-\mathrm{z}_{2}\right) \ldots \ldots .\left(\mathrm{z}-\mathrm{z}_{9}\right)$
put z = 1
$\lim _{z \rightarrow 1} \frac{z^{10}-1}{(z-1)}=\left(1-z_{1}\right)\left(1-z_{2}\right) \ldots\left(1-z_{9}\right)$
$\lim _{z \rightarrow 1} \frac{10 z^{9}}{1}=\left(1-z_{1}\right)\left(1-z_{2}\right) \ldots\left(1-z_{9}\right)$
$=\left|\left(1-z_{1}\right)\left(1-z_{2}\right) \ldots .\left(1-z_{9}\right)\right|=10$
(S) $1+\cos \frac{2 \pi}{10}+\cos \frac{4 \pi}{10}+\ldots \ldots+\cos \frac{18 \pi}{10}=0$
since they are sum of ten, tenth roots of unity
$\sum_{k=1}^{9} \cos \left(\frac{2 k \pi}{10}\right)=-1$
$1+1=2$
Q.
[JEE 2015, 8(Each 2M, –1M)]
[JEE 2015, 8(Each 2M, –1M)]
Ans. ((A) p,q (B) p,q (C) p,q,s,t (D) q,t)
(A) $\left|\frac{\alpha \sqrt{3}+\beta}{2}\right|=\sqrt{3} \Rightarrow \alpha \sqrt{3}+\frac{\alpha-2}{\sqrt{3}}=\pm 2 \sqrt{3}$
$\Rightarrow \alpha\left(\frac{4}{\sqrt{3}}\right)=\frac{2}{\sqrt{3}} \pm 2 \sqrt{3}$
$\alpha=2,-1 \Rightarrow|\alpha|=1,2$
(B) By continuity $\quad-3 a-2=b+a^{2}$
By differentiability $-6 a=b$
$\quad a^{2}-3 a+2=0 \Rightarrow a=1,2$
(C) $\quad\left(\left(-3+2 \omega+3 \omega^{2}\right) \omega\right)^{4 \mathrm{n}+3}+\left(\left(-3+2 \omega+3 \omega^{2}\right) \omega^{2}\right)^{4 n+3}+\left(\left(-3+2 \omega+3 \omega^{2}\right)^{4 n+3}\right)=0$
$\quad \Rightarrow\left(-3+2 \omega+3 \omega^{2}\right)^{4 n+3}\left[\omega^{4 n+3}+\omega^{8 n+6}+1\right]=0$
$\quad \Rightarrow \omega^{\mathrm{n}}+\omega^{2 \mathrm{n}}+1=0 \Rightarrow n$ is not a multiple of 3
$\begin{aligned} \text { (D) } \frac{2 a b}{a+b}=4,2(5-a) &=b-5 \\ b &=15-2 a \\ 2 a(15-2 a)=4(15-a) & \Rightarrow 15 a-2 a^{2}=30-2 a \\ 2 a^{2}-17 a+30=0 & \Rightarrow 2 a^{2}-12 a-5 a+30=0 \\ 2 a(a-6)-5(a-6) &=0 \end{aligned}$
$\mathrm{a}=\frac{5}{2}, 6$
$\Rightarrow|\mathrm{q}-\mathrm{a}|=|10-2 \mathrm{a}|=5 \mathrm{or} 2$
Q. For any integer $\mathrm{k},$ let $\alpha_{\mathrm{k}}=\cos \left(\frac{\mathrm{k} \pi}{7}\right)+\mathrm{i} \sin \left(\frac{\mathrm{k} \pi}{7}\right),$ where $\mathrm{i}=\sqrt{-1} .$ The value of the expression
$\frac{\sum_{\mathrm{k}=1}^{12}\left|\alpha_{\mathrm{k}+1}-\alpha_{\mathrm{k}}\right|}{\sum_{\mathrm{k}=1}^{3}\left|\alpha_{4 \mathrm{k}-1}-\alpha_{4 \mathrm{k}-2}\right|}$ is
[JEE 2015, 4M, –0M]
Ans. 4
$\alpha_{\mathrm{k}}$ are vertices of 14 sided regular polygon.
$\left|\alpha_{\mathrm{k}+1}-\alpha_{\mathrm{k}}\right|$ length of a side of the regular polygon
$\left|\alpha_{4 \mathrm{k}-1}-\alpha_{4 \mathrm{k}-2}\right|$ length of a side of the regular polygon
$\Rightarrow \quad \frac{12(\mathrm{S})}{3(\mathrm{S})}=4$
Alter
$\alpha_{\mathrm{k}}=\cos \left(\frac{\mathrm{k} \pi}{7}\right)+\mathrm{i} \sin \left(\frac{\mathrm{k} \pi}{7}\right)=e^{\mathrm{i} \frac{\mathrm{k} \pi}{7}}$
$\alpha_{\mathrm{k}+1}=e^{\frac{i(k+1) \pi}{7}}$
Q. Let $z=\frac{-1+\sqrt{3} i}{2},$ where $i=\sqrt{-1},$ and $r, s \in\{1,2,3\} .$ Let $P=\left[\begin{array}{cc}{(-z)^{\mathrm{r}}} & {z^{2 s}} \\ {z^{2 s}} & {z^{\mathrm{r}}}\end{array}\right]$ and I be the identity matrix of order $2 .$ Then the total number of ordered pairs (r,s) for which $P^{2}=-I$ is
[JEE(Advanced 2016]
Ans. 1
Q. Let $a, b \in \square$ and $a^{2}+b^{2} \neq 0 .$ Suppose $S=\left\{z \in \square: z=\frac{1}{a+i b t}, t \in \square, t \neq 0\right\},$ where $i=\sqrt{-1}$ If $z=x+$ iy and $z \in S,$ then $(x, y)$ lies on
(A) the circle with radius $\frac{1}{2 \mathrm{a}}$ and centre $\left(\frac{1}{2 \mathrm{a}}, 0\right)$ for $\mathrm{a}>0, \mathrm{b} \neq 0$
(B) the circle with radius $-\frac{1}{2 \mathrm{a}}$ and centre $\left(-\frac{1}{2 \mathrm{a}}, 0\right)$ for a $<0, \mathrm{b} \neq 0$
(C) the $\mathrm{x}$ -axis for $\mathrm{a} \neq 0, \mathrm{b}=0$
(D) the y-axis for a $=0, \mathrm{b} \neq 0$
[JEE(Advanced 2016]
Ans. (A,C,D)
Q. Let $a, b, x$ and $y$ be real numbers such that $a-b=1$ and $y \neq 0 .$ If the complex number $z=x+i y$ satisfies $\operatorname{Im}\left(\frac{a z+b}{z+1}\right)=y,$ then which of the following is (are) possible value(s) of $x ?$
(A) $-1-\sqrt{1-\mathrm{y}^{2}}$
(B) $1+\sqrt{1+y^{2}}$
(C) $1-\sqrt{1+y^{2}}$
(D) $-1+\sqrt{1-y^{2}}$
[JEE(Advanced 2017]
Ans. (A,D)
$\operatorname{Im}\left(\frac{\mathrm{az}+\mathrm{b}}{\mathrm{z}+1}\right)=\mathrm{y}$ and $\mathrm{z}=\mathrm{x}+\mathrm{iy}$
$\therefore \quad \operatorname{Im}\left(\frac{\mathrm{a}(\mathrm{x}+\mathrm{iy})+\mathrm{b}}{\mathrm{x}+\mathrm{iy}+1}\right)=\mathrm{y}$
$\Rightarrow \quad \operatorname{Im}\left(\frac{(a x+b+i a y)(x+1-i y)}{(x+1)^{2}+y^{2}}\right)=y$
$\begin{aligned} \Rightarrow &-\mathrm{y}(\mathrm{ax}+\mathrm{b})+\mathrm{ay}(\mathrm{x}+1)=\mathrm{y}\left((\mathrm{x}+1)^{2}+\mathrm{y}^{2}\right) \\ \Rightarrow &(\mathrm{a}-\mathrm{b}) \mathrm{y}=\mathrm{y}\left((\mathrm{x}+1)^{2}+\mathrm{y}^{2}\right) \\ & \because \mathrm{y} \neq 0 \text { and } \mathrm{a}-\mathrm{b}=1 \\ \Rightarrow &(\mathrm{x}+1)^{2}+\mathrm{y}^{2}=1 \end{aligned}$
$\Rightarrow \quad x=-1 \pm \sqrt{1-y^{2}}$
Q. For a non-zero complex number z, let arg(z) denotes the principal argument with $-\pi<\arg (\mathrm{z}) \leq \pi$. Then, which of the following statement(s) is (are) FALSE ?
(A) $\arg (-1-i)=\frac{\pi}{4},$ where $i=\sqrt{-1}$
(B) The function $f: \square \rightarrow(-\pi, \pi],$ defined by $f(\mathrm{t})=\arg (-1+i t)$ for all $t \in \square,$ is continuous at all points of $\square,$ where $i=\sqrt{-1}$
(C) For any two non-zero complex numbers $z_{1}$ and $z_{2}, \arg \left(\frac{z_{1}}{z_{2}}\right)-\arg \left(z_{1}\right)+\arg \left(z_{2}\right)$ is an integer multiple of $2 \pi$
(D) For any three given distinct complex numbers $z_{1}, z_{2}$ and $z_{3}$, the locus of the point z satisfying the condition $\arg \left(\frac{\left(z-z_{1}\right)\left(z_{2}-z_{3}\right)}{\left(z-z_{3}\right)\left(z_{2}-z_{1}\right)}\right)=\pi,$ lies on a straight line(D) For any three given distinct complex numbers $z_{1}, z_{2}$ and $z_{3}$, the locus of the point z satisfying the condition $\arg \left(\frac{\left(z-z_{1}\right)\left(z_{2}-z_{3}\right)}{\left(z-z_{3}\right)\left(z_{2}-z_{1}\right)}\right)=\pi,$ lies on a straight line
[JEE(Advanced 2018]
Ans. (A,B,D)
(A) $\arg (-1-i)=-\frac{3 \pi}{4}$
(B) $f(\mathrm{t})=\arg (-1+\mathrm{i} \mathrm{t})=\left\{\begin{array}{ll}{\pi-\tan ^{-1}(\mathrm{t}),} & {\mathrm{t} \geq 0} \\ {-\pi+\tan ^{-1}(\mathrm{t}),} & {\mathrm{t} \geq 0}\end{array}\right.$
Discontinuous at $\mathrm{t}=0$
(C) $\arg \left(\frac{\mathrm{z}_{1}}{\mathrm{z}_{2}}\right)-\arg \left(\mathrm{z}_{1}\right)+\arg \left(\mathrm{z}_{2}\right)$
$=\arg \mathrm{g}_{1}-\arg \left(\mathrm{z}_{2}\right)+2 \mathrm{n} \pi-\arg \left(\mathrm{z}_{1}\right)+\arg \left(\mathrm{z}_{2}\right)=2 \mathrm{n} \pi$
(D) $\arg \left(\frac{\left(\mathrm{z}-\mathrm{z}_{1}\right)\left(\mathrm{z}_{2}-\mathrm{z}_{3}\right)}{\left(\mathrm{z}-\mathrm{z}_{3}\right)\left(\mathrm{z}_{2}-\mathrm{z}_{1}\right)}\right)=\pi$
$\Rightarrow \frac{\left(\mathrm{z}-\mathrm{z}_{1}\right)\left(\mathrm{z}_{2}-\mathrm{z}_{3}\right)}{\left(\mathrm{z}-\mathrm{z}_{3}\right)\left(\mathrm{z}_{2}-\mathrm{z}_{1}\right)}$ is real.
$\Rightarrow \mathrm{z}, \mathrm{z}_{1}, \mathrm{z}_{2}, \mathrm{z}_{3}$ are concyclic.
Q. Let $s, t, r$ be the non-zero complex numbers and $L$ be the set of solutions $z=x+i y$ $(x, y \in \square, i=\sqrt{-1})$ of the equation $s z+t \bar{z}+r=0,$ where $\bar{z}=x-i y .$ Then, which of the following statement(s) is (are) TRUE?
(A) If L has exactly one element, then $|s| \neq|t|$
(B) If $|s|=|t|,$ then $L$ has infinitely many elements
(C) The number of elements in L\cap $\{z:|z-1+i|=5\}$ is at most 2
(D) If L has more than one element, then L has infinitely many elements
[JEE(Advanced 2018]
Ans. (A,C,D)
