JEE Advanced Previous Year Questions of Physics with Solutions are available at eSaral. Practicing JEE Advanced Previous Year Papers Questions of Physics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
Get detailed Class 11th & 12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Click Here for JEE main Previous Year Topic Wise Questions of Physics with Solutions
Download eSaral app for free study material and video tutorials.
Simulator
Previous Years JEE Advanced Questions
Paragraph 2
Consider an evacuated cylindrical chamber of height h having rigid conducting plates at the ends and an insulating curved surface as shown in the figure. A number of spherical balls made of a light weight and soft material and coated with a conducting material are placed on the bottom plate. The balls have a radius r <
Q.For the circuit shown in the figure -
(A) the current I through the battery is 7.5 mA
(B) the potential difference across $\mathrm{R}_{\mathrm{L}}$ is 18V
(C) ratio of powers dissipated in $\mathrm{R}_{1}$ and $\mathrm{R}_{2}$ is 3
(D) if $\mathrm{R}_{1}$ and $\mathrm{R}_{2}$ are interchanged, magnitude of the power dissipated in $\mathrm{R}_{\mathrm{L}}$ will decrease by a factor of 9
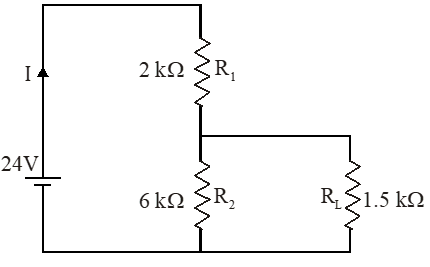[IIT-JEE 2009]
[IIT-JEE 2009]
Ans. (A,D)
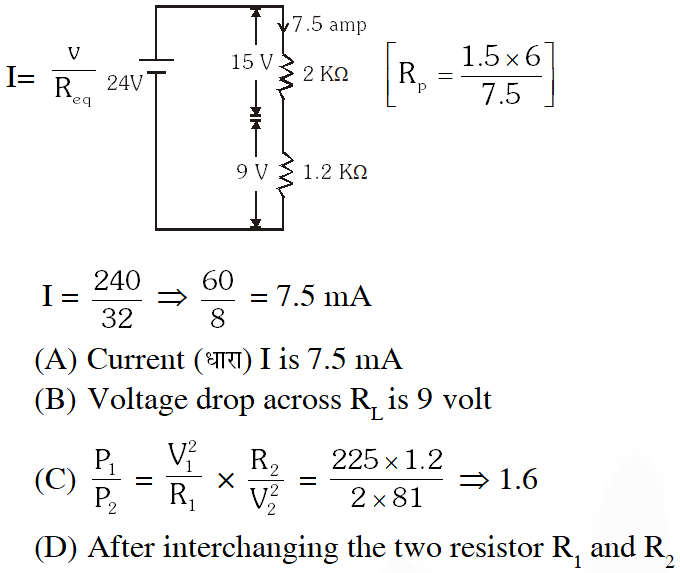
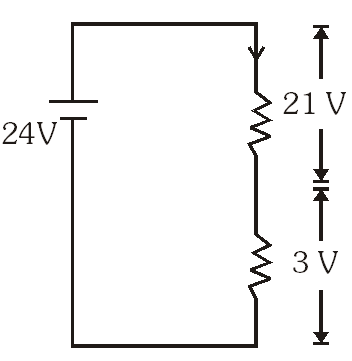
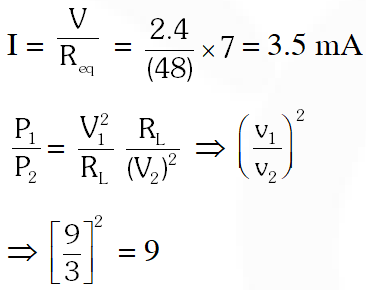
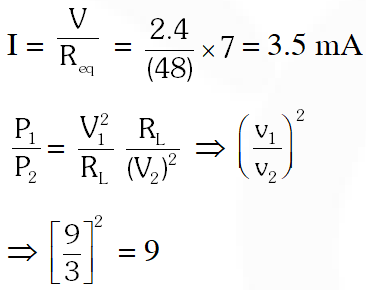
Q. Incandescent bulbs are designed by keeping in mind that the resistance of their filament increases with the increase in temperature. If at room temperature, 100 W, 60 W and 40 W bulbs have filament resistance $\mathrm{R}_{100} \cdot \mathrm{R}_{60} \mathrm{and} \mathrm{R}_{40}$, respectively, the relation between these resistances is –
$(\mathrm{A}) \frac{1}{\mathrm{R}_{100}}=\frac{1}{\mathrm{R}_{40}}+\frac{1}{\mathrm{R}_{60}}$
$(\mathrm{B}) \mathrm{R}_{100}=\mathrm{R}_{40}+\mathrm{R}_{60}$
(C) $\mathrm{R}_{100}>\mathrm{R}_{60}>\mathrm{R}_{40}$
$(\mathrm{D}) \frac{1}{\mathrm{R}_{100}}>\frac{1}{\mathrm{R}_{60}}>\frac{1}{\mathrm{R}_{40}}$
[IIT-JEE 2010]
Ans. (D)
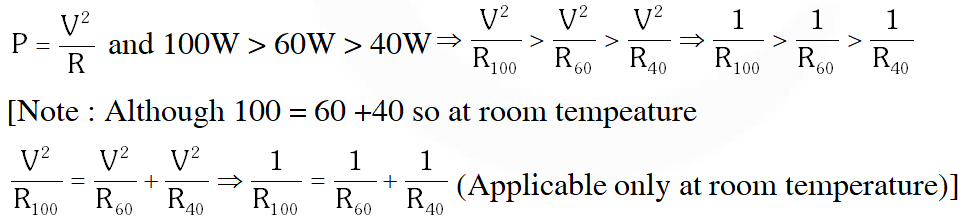
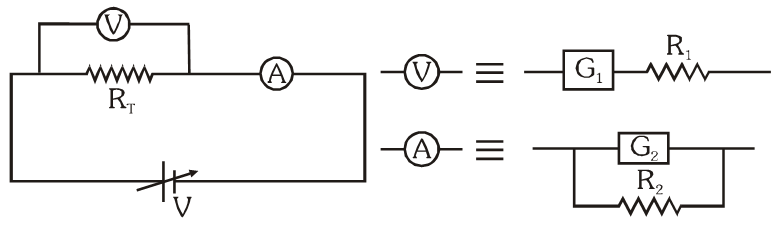
Q. To verify Ohm’s law, a student is provided with a test resistor $\mathrm{R}_{\mathrm{T}}$, a high resistance $R_{1}$, a small resistance $\mathrm{R}_{2}$, two identical galvanometers $\mathrm{G}_{1}$ and $\mathrm{G}_{2}$, and a variable voltage source V. The correct circuit to carry out the experiment is :–
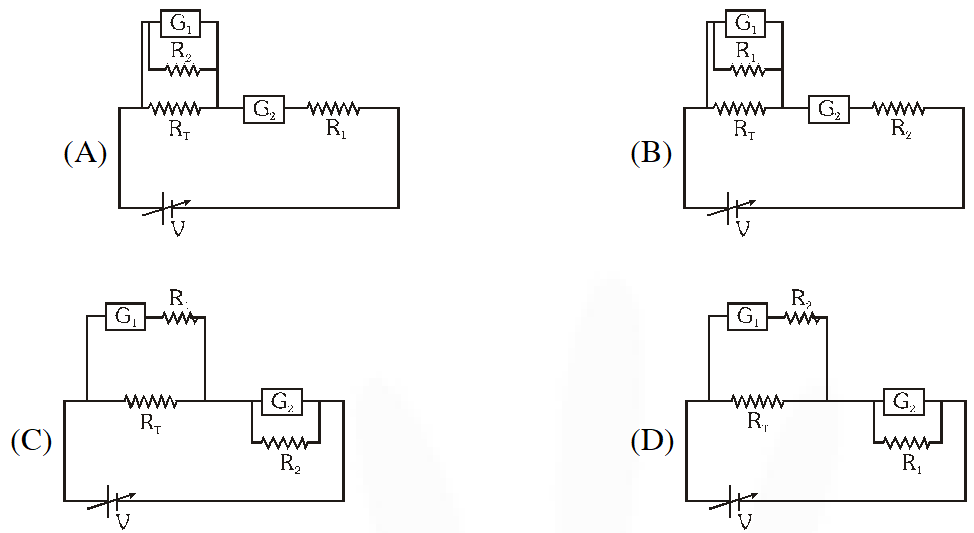[IIT-JEE 2010]
[IIT-JEE 2010]
Ans. (C)
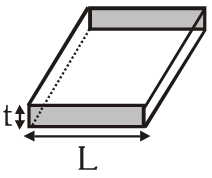
Q. Consider a thin square sheet of side L and thickness t, made of a material of resistivity . The resistance between two opposite faces, shown by the shaded areas in the figure is –
(A) directly proportional to L
(B) directly proportional to t
(C) independent of L
(D) independent of t
[IIT-JEE 2010]
(A) directly proportional to L
(B) directly proportional to t
(C) independent of L
(D) independent of t
[IIT-JEE 2010]
Ans. (C)
$\mathrm{R}=\frac{\rho \mathrm{L}}{\mathrm{A}}=\frac{\rho \mathrm{L}}{\mathrm{Lt}}=\frac{\rho}{\mathrm{t}} \Rightarrow$ independent of $\mathrm{L}$
Q. When two identical batteries of internal resistance $1 \Omega$ each are connected in series across a resistor R, the rate of heat produced in R is $\mathbf{J}_{1}$. When the same batteries are connected in parallel across R, the rate is $\mathrm{J}_{2} \cdot$ If $\mathrm{J}_{1}=2.25 \mathrm{J}_{2}$ then the value of R in $\Omega$ is –
[IIT-JEE 2010]
Ans. 4
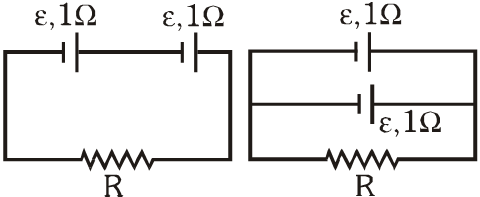$J_{1}=\left(\frac{2 \varepsilon}{R+2}\right)^{2} R$ and $J_{2}=\left(\frac{\varepsilon}{R+1 / 2}\right)^{2} R$ as $\frac{J_{1}}{J_{2}}=2.25$ so $\frac{4 \varepsilon^{2}}{(R+2)}=2.25 \frac{4 \varepsilon^{2}}{(1+2 R)^{2}} \Rightarrow R=4 \Omega$
$J_{1}=\left(\frac{2 \varepsilon}{R+2}\right)^{2} R$ and $J_{2}=\left(\frac{\varepsilon}{R+1 / 2}\right)^{2} R$ as $\frac{J_{1}}{J_{2}}=2.25$ so $\frac{4 \varepsilon^{2}}{(R+2)}=2.25 \frac{4 \varepsilon^{2}}{(1+2 R)^{2}} \Rightarrow R=4 \Omega$
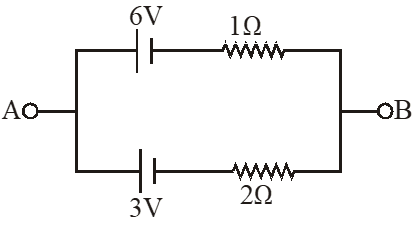
Q. Two batteries of different emfs and different internal resistances are connected as shown. The voltage across AB in volts is –
[IIT-JEE 2011]
[IIT-JEE 2011]
Ans. 5
$E_{A B}=\frac{\frac{E_{1}}{R_{1}}+\frac{E_{2}}{R_{2}}}{\frac{1}{R_{1}}+\frac{1}{R_{2}}}=\frac{\frac{6}{1}+\frac{3}{2}}{\frac{1}{1}+\frac{1}{2}}=\frac{\frac{15}{2}}{\frac{3}{2}}=5$ volt
Q. A meter bridge is set-up as shown, to determine an unknown resistance ‘X’ using a standard 10 ohm resistor. The galvanometer shows point when tapping-key is at 52 cm mark. The end-corrections are 1 cm and 2 cm respectively for the ends A and B. The determined value of ‘X’ is-
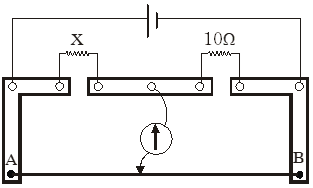(A) 10.2 ohm (B) 10.6 ohm (C) 10.8 ohm (D) 11.1 ohm
[IIT-JEE 2011]
(A) 10.2 ohm (B) 10.6 ohm (C) 10.8 ohm (D) 11.1 ohm
[IIT-JEE 2011]
Ans. (B)
Apply condition of wheatstone bridge, $\frac{x}{52+1}=\frac{10}{48+2} \Rightarrow x=\frac{10}{50} \times 53 \Rightarrow \mathrm{x}=10.6 \Omega$
Q. For the resistance network shown in the figure, choose the correct option(s).
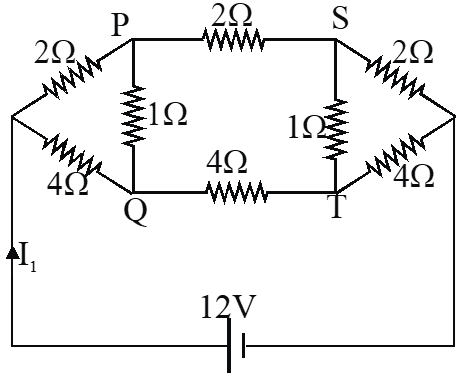(A) the current through PQ is zero
(B) $\mathrm{I}_{1}=3 \mathrm{A}$
(C) The potential at S is less than that at Q
(D) $\mathrm{I}_{2}=2 \mathrm{A}$
[IIT-JEE 2012]
(A) the current through PQ is zero
(B) $\mathrm{I}_{1}=3 \mathrm{A}$
(C) The potential at S is less than that at Q
(D) $\mathrm{I}_{2}=2 \mathrm{A}$
[IIT-JEE 2012]
Ans. (A,B,C,D)
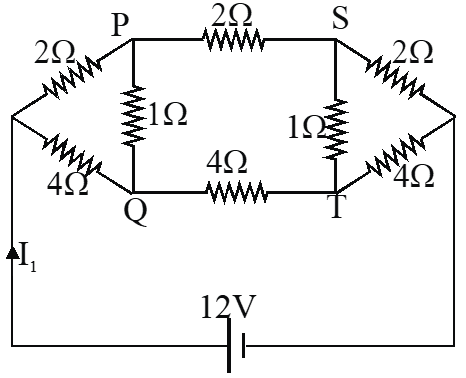Since resitances in two arms upper and lower are in same ratio.
Current through PQ is zero.
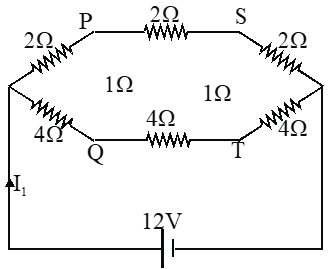$I_{2}=\frac{12}{6}=2 A$, $I_{1}=\frac{12}{6}+\frac{12}{12}=3 A$ and Potential of $\mathrm{S}$ is less than that at $\mathrm{Q}$
Since resitances in two arms upper and lower are in same ratio.
Current through PQ is zero.
$I_{2}=\frac{12}{6}=2 A$, $I_{1}=\frac{12}{6}+\frac{12}{12}=3 A$ and Potential of $\mathrm{S}$ is less than that at $\mathrm{Q}$
Q. Heater of an electric kettle is made of a wire of length L and diameter d. It takes 4 minutes to raise the temperature of 0.5 kg water by 40 K. This heater is replaced by a new heater having two wires of the same material, each of length L and diameter 2d. The way these wires are connected is given in the options. How much time in minutes will it take to raise the temperature of the same amount of water by 40 K ?
(A) 4 if wires are in parallel
(B) 2 if wires are in series
(C) 1 if wires are in series
(D) 0.5 if wires are in parallel
[JEE Advanced 2014]
Ans. (B,D)
Resistance of heater $1, \mathrm{R}=\frac{4 \rho \mathrm{L}}{\pi \mathrm{d}^{2}}$
Resistance of heater $2, R_{1}=\frac{R}{4}, R_{2}=\frac{R}{4}$
Series $\mathrm{R}_{\mathrm{net}}=\frac{\mathrm{R}}{2}$
Power $=2 \frac{\mathrm{V}^{2}}{\mathrm{R}}$
$\Rightarrow \quad$ power is twice, hence time is $\frac{1}{2}$
time $=\frac{1}{2}$ of $4 \min =2 \min$
Parallel $\mathrm{R}_{\mathrm{Net}}=\frac{\mathrm{R}}{8}$
Power = 8 times
time $=\frac{\mathrm{R}}{8}$ times $=\frac{\mathrm{R}}{8} \times 4 \min =0.5 \mathrm{sec}$
Q. Two ideal batteries of emf $\mathrm{V}_{1}$ and $\mathrm{V}_{2}$ and three resistances $\mathrm{R}_{1}, \mathrm{R}_{2}$ and $\mathrm{R}_{3}$ are connected as shown in the figure. The current in resistance $\mathrm{R}_{2}$ would be zero if :-
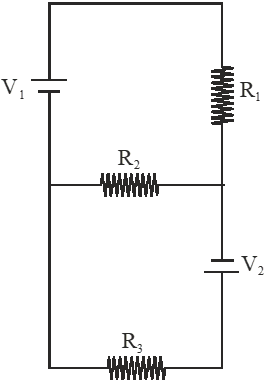(A) $\mathrm{V}_{1}=\mathrm{V}_{2}$ and $\mathrm{R}_{1}=\mathrm{R}_{2}=\mathrm{R}_{3}$
(B) $\mathrm{V}_{1}=\mathrm{V}_{2}$ and $\mathrm{R}_{1}=2 \mathrm{R}_{2}=\mathrm{R}_{3}$
(C) $\mathrm{V}_{1}=2 \mathrm{V}_{2}$ and $2 \mathrm{R}_{1}=2 \mathrm{R}_{2}=\mathrm{R}_{3}$
(D) $2 \mathrm{V}_{1}=\mathrm{V}_{2}$ and $2 \mathrm{R}_{1}=\mathrm{R}_{2}=\mathrm{R}_{3}$
[JEE Advanced 2014]
(A) $\mathrm{V}_{1}=\mathrm{V}_{2}$ and $\mathrm{R}_{1}=\mathrm{R}_{2}=\mathrm{R}_{3}$
(B) $\mathrm{V}_{1}=\mathrm{V}_{2}$ and $\mathrm{R}_{1}=2 \mathrm{R}_{2}=\mathrm{R}_{3}$
(C) $\mathrm{V}_{1}=2 \mathrm{V}_{2}$ and $2 \mathrm{R}_{1}=2 \mathrm{R}_{2}=\mathrm{R}_{3}$
(D) $2 \mathrm{V}_{1}=\mathrm{V}_{2}$ and $2 \mathrm{R}_{1}=\mathrm{R}_{2}=\mathrm{R}_{3}$
[JEE Advanced 2014]
Ans. (A,B,D)
since current through $\mathrm{R}_{2}$ is zero
Hence $\left[\frac{\mathrm{V}_{1}}{\mathrm{R}_{1}}=\frac{\mathrm{V}_{2}}{\mathrm{R}_{3}}\right]$
The above equation is satisfied by options (A, B, D)
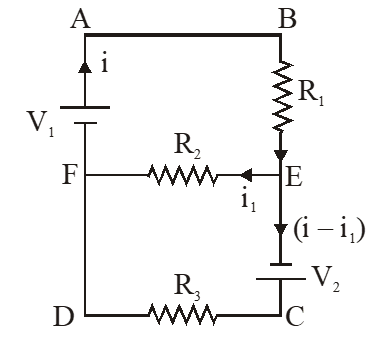
Q. A galvanometer gives full scale deflection with 0.006 A current. By connecting it to a $4990 \Omega$ resistance, it can be converted into a voltmeter of range 0 - 30 V. If connected to a $\frac{2 \mathrm{n}}{249} \Omega$ resistance, it becomes an ammeter of range 0 - 1.5 A. The value of n is :-
[JEE Advanced 2014]
Ans. (5)
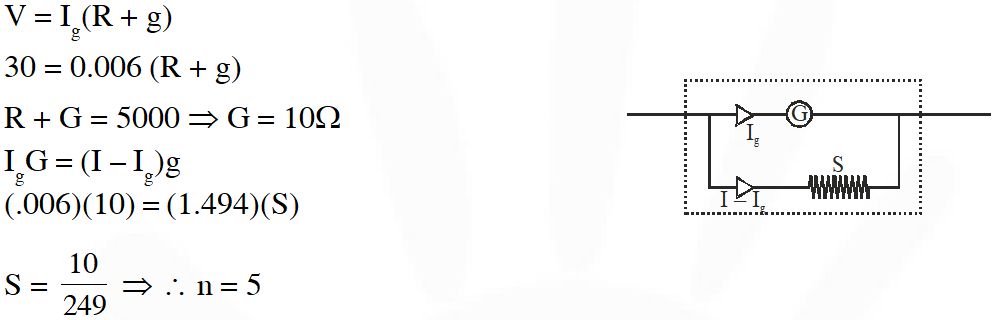
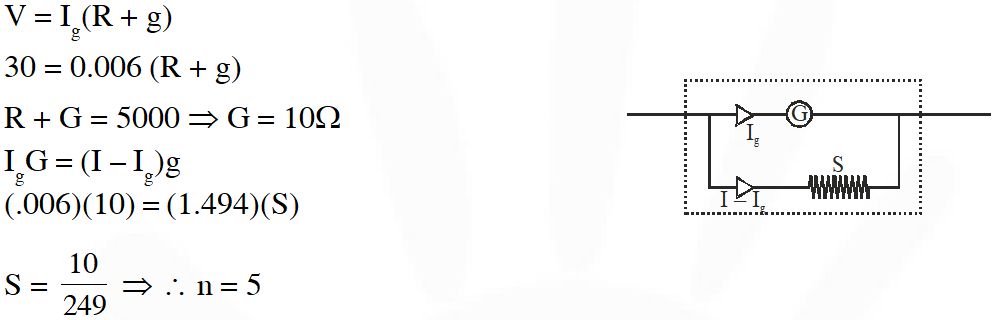
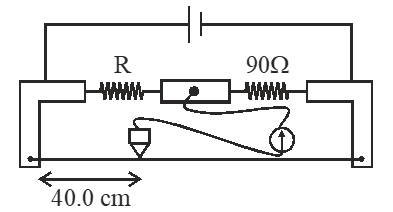
Q. During an experiment with a metre bridge, the galvanometer shows a point when the jockey is pressed at 40.0 cm using a standard resistance of $90 \Omega$, as shown in the figure. The least count of the scale used in the metre bridge is 1mm. The unknown resistance is :-
(A) $60 \pm 0.15 \Omega$
(B) $135 \pm 0.56 \Omega$
(C) $60 \pm 0.25 \Omega$
(D) $135 \pm 0.23 \Omega$
[JEE Advanced 2014]
(A) $60 \pm 0.15 \Omega$
(B) $135 \pm 0.56 \Omega$
(C) $60 \pm 0.25 \Omega$
(D) $135 \pm 0.23 \Omega$
[JEE Advanced 2014]
Ans. (C)
For meter bridge,
$\mathrm{R}=\mathrm{X}\left(\frac{\ell}{100-\ell}\right)$
$=90\left(\frac{\ell}{100-\ell}\right)$
$=90\left(\frac{40}{60}\right)$v
$=60 \Omega$
error in R : (erro = least count)
$\frac{\mathrm{d} \mathrm{R}}{\mathrm{R}}=\frac{\mathrm{d} \mathrm{x}}{\mathrm{x}}+\frac{\mathrm{d} \ell}{\ell}+\frac{\mathrm{d}(100-\ell)}{(100-\ell)}$
$=0+\frac{\operatorname{lmm}}{40 \mathrm{cm}}+\frac{1 \mathrm{mm}}{60 \mathrm{cm}}$
Q. An infinite line charge of uniform electric charge density $\lambda$ lies along the axis of an electrically conducting infinite cylindrical shell of radius R. At time t = 0, the space inside the cylinder is filled with a material of permittivity $\varepsilon$ and electrical conductivity $\sigma$. The electrical conduction in the material follows Ohm's law. Which one of the following graphs best describes the
subsequent variation of the magnitude of current density j(t) at any point in the material?
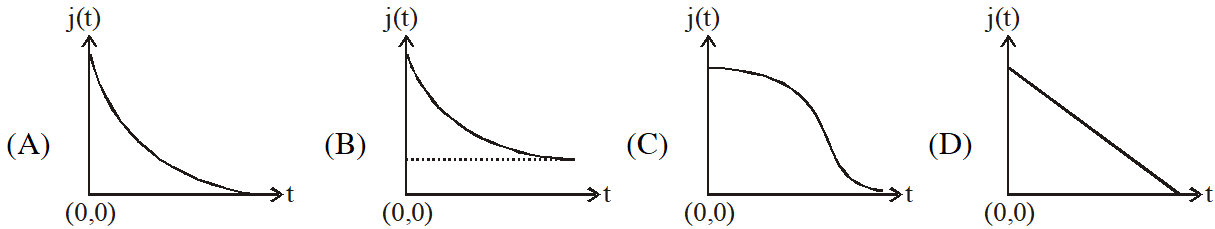[JEE Advanced 2016]
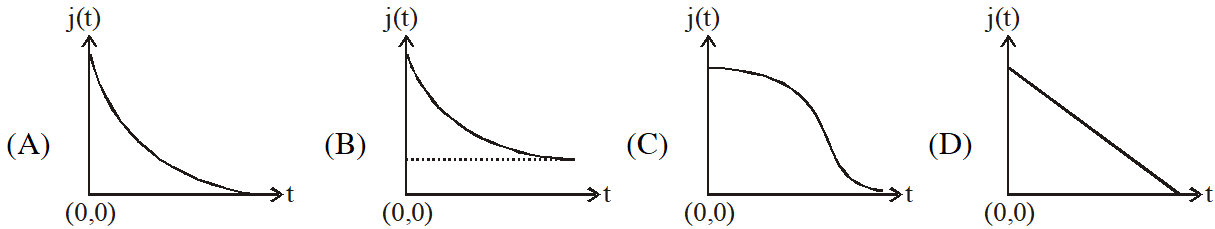[JEE Advanced 2016]
Ans. (A)
This is the problem of RC circuit where the product RC is a constant.
So due to leakage current, charge & current density will exponentially decay & will become zero at infinite time. So correct answer is (A)
for any small element
Resistance $\mathrm{R}=\frac{\mathrm{dr}}{\sigma(2 \pi r \ell)}$
Capacitance $\mathrm{C}=\frac{\in 2 \pi \mathrm{r} \ell}{\mathrm{dr}}$
Product $\mathrm{R} \times \mathrm{C}=\frac{\epsilon}{\sigma}=\mathrm{constant}$
$\mathrm{q}=\mathrm{q}_{0} \mathrm{e}^{-\left(\frac{\mathrm{t} \sigma}{\epsilon}\right)}$
$\mathrm{I}=\frac{\mathrm{d} q}{\mathrm{dt}}=\frac{\mathrm{q}_{0} \sigma}{\epsilon} \mathrm{e}^{-\left(\frac{\mathrm{t} \sigma}{\epsilon}\right)}$
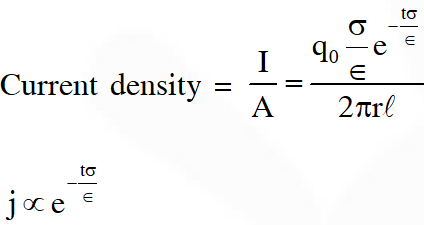
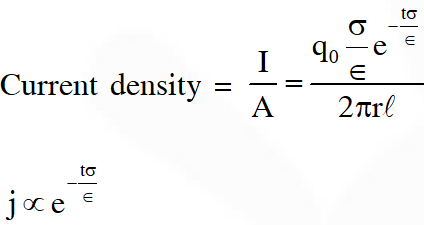
Q. An incandescent bulb has a thin filament of tungsten that is heated to high temperature by passing an electric current. The hot filament emits black-body radiation. The filament is observed to break up at random locations after a sufficiently long time of operation due to non-uniform evaporation of tungsten from the filament. If the bulb is powered at constant voltage, which of the following statement(s) is(are) true?
(A) The temperature distribution over the filament is uniform
(B) The resistance over small sections of the filament decreases with time
(C) The filament emits more light at higher band of frequencies before it breaks up
(D) The filament consumes less electrical power towards the end of the life of the bulb
[JEE Advanced 2016]
Ans. (C,D)
Because of non-uniform evaporation at different section, area of cross-section would be different at different sections.
Region of highest evaporation rate would have rapidly reduced area and would become break up cross-section.
Resistance of the wire as whole increases with time.
Overall resistance increases hence power decreases. At break up junction temperature would be highest, thus light of highest band frequency would be emitted at those cross-section.
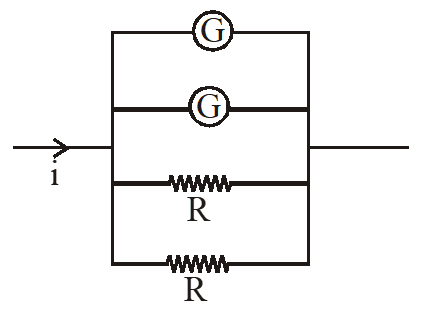
Q. Consider two identical galvanometers and two identical resistors with resistance R. If the internal resistance of the galvanometers $\mathrm{R}_{\mathrm{c}}<\mathrm{R} / 2$, which of the following statement(s) about any one of the galvanometers is(are) true
(A) The maximum voltage range is obtained when all the components are connected in series
(B) The maximum voltage range is obtained when the two resistors and one galvanometer are connected in series, and the second galvanometer is connected in parallel to the first galvanometer
(C) The maximum current range is obtained when all the components are connected in parallel
(D) The maximum current range is obtained when the two galvanometers are connected in series and the combination is connected in parallel with both the resistors.
[JEE Advanced 2016]
Ans. (B,C)
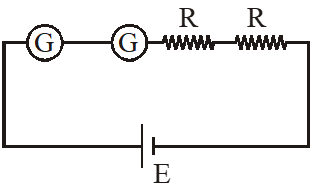Range $=\mathrm{i}_{\mathrm{g}}\left(2 \mathrm{R}_{\mathrm{C}}+2 \mathrm{R}\right)$
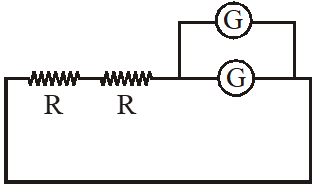
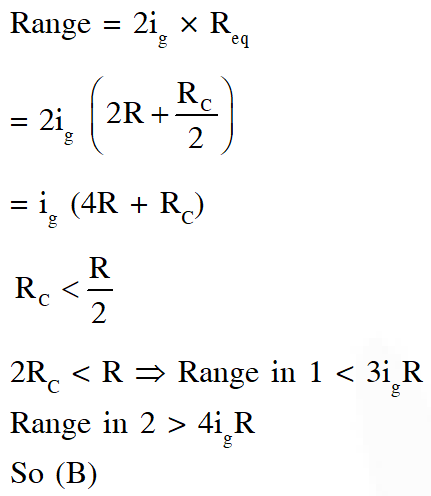
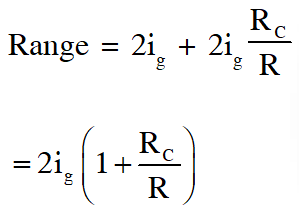
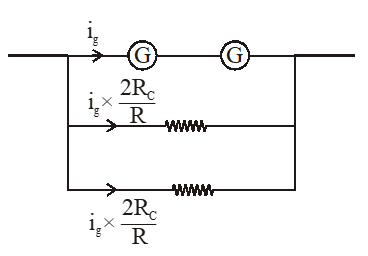Range $=\mathrm{i}_{\mathrm{g}}+4 \mathrm{i}_{\mathrm{g}} \frac{\mathrm{R}_{\mathrm{C}}}{\mathrm{R}}$
$=2 \mathrm{i}_{\mathrm{g}}\left[\frac{1}{2}+\frac{2 \mathrm{R}_{\mathrm{c}}}{\mathrm{R}}\right]$
$=2 \mathrm{i}_{\mathrm{g}}\left(\frac{1}{2}+\frac{\mathrm{R}_{\mathrm{C}}}{\mathrm{R}}+\frac{\mathrm{R}_{\mathrm{C}}}{\mathrm{R}}\right)$
So (C)
Range $=\mathrm{i}_{\mathrm{g}}\left(2 \mathrm{R}_{\mathrm{C}}+2 \mathrm{R}\right)$
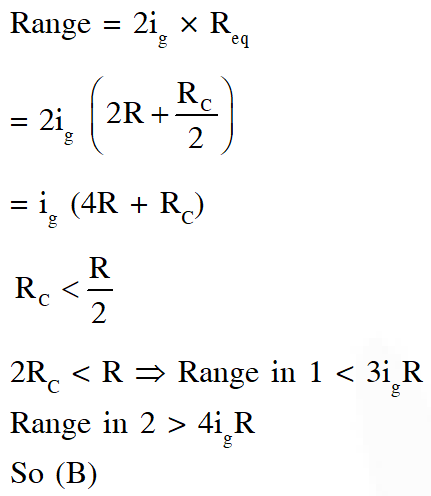
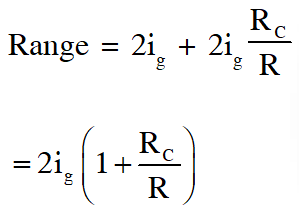
Range $=\mathrm{i}_{\mathrm{g}}+4 \mathrm{i}_{\mathrm{g}} \frac{\mathrm{R}_{\mathrm{C}}}{\mathrm{R}}$
$=2 \mathrm{i}_{\mathrm{g}}\left[\frac{1}{2}+\frac{2 \mathrm{R}_{\mathrm{c}}}{\mathrm{R}}\right]$
$=2 \mathrm{i}_{\mathrm{g}}\left(\frac{1}{2}+\frac{\mathrm{R}_{\mathrm{C}}}{\mathrm{R}}+\frac{\mathrm{R}_{\mathrm{C}}}{\mathrm{R}}\right)$
So (C)
Q.
Which of the following statements is correct ?
(A) The balls will bounce back to the bottom plate carrying the opposite charge they went up with
(B) the balls will execute simple harmonic motion between the two plates
(C) The balls will bounce back to the bottom plate carrying the same charge they went up with
(D) The balls will stick to the top plate and remain there
[JEE Advanced 2016]
Ans. (A)
Balls placed on +ve plate become positive charge and move upward due to electric field.
These balls on colliding with negative plate become negatively charged and move opposite to the direction of electric field.
Q. The average current in the steady state registered by the ammeter in the circuit will be :
(A) Proportional to $\mathrm{V}_{0}^{1 / 2}$
(B) Proportional to $V_{0}^{2}$
(C) Proportional to the potential $\mathrm{V}_{0}$
(D) Zero
[JEE Advanced 2016]
Ans. (B)
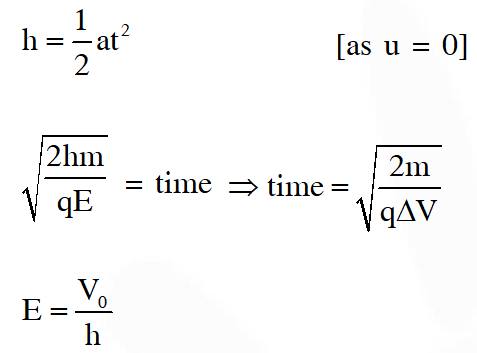
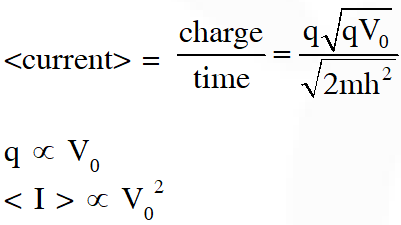
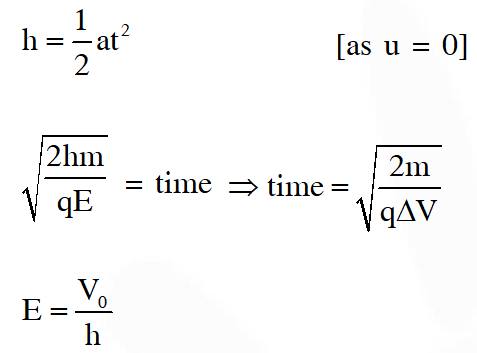
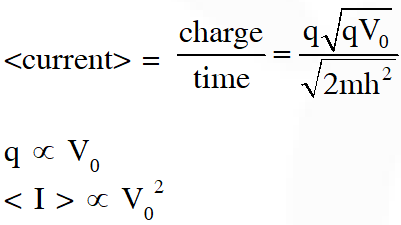
Comments
Ayub K
April 22, 2024, 6:35 a.m.
solution given for Q1 is wrong . The ratio of PR1/PR2 is asked to find out . But in answer , the combined R2 and RL is taken in the solution . Similar is the final power ratio RL
Chetan Sharma
May 7, 2021, 12:04 p.m.
sir please please upload the all previous year questions of jee advance , chapter wise
Sunita
Sept. 22, 2020, 4:49 p.m.
We need after 2016 questions but really questions and there explanations are good
DEVANSH SINGHANIA
Aug. 18, 2020, 10:40 p.m.
fan of esaral questions of jee are very well mannered arranged