JEE Main Previous Year Question of Physics with Solutions are available here. Practicing JEE Main Previous Year Papers Questions of Physics will help all the JEE aspirants in realizing the question pattern as well as help in analyzing their weak & strong areas.
Get detailed Class 11th &12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Simulator
Previous Years AIEEE/JEE Main Questions
Q. Statement–1 : The temperature dependence of resistance is usually given as $\mathrm{R}=\mathrm{R}_{0}(1+\alpha \Delta \mathrm{t})$. The resistance of a wire changes from $100 \Omega$ to $150 \Omega$ when its temperature is increased from $27^{\circ} \mathrm{C}$ to $227^{\circ} \mathrm{C}$. This implies that = $2.5 \times 10^{-3} /^{\circ} \mathrm{C}$.
Statement–2 : $\mathrm{R}=\mathrm{R}_{0}(1+\alpha \Delta \mathrm{t})$ is valid only when the change in the temperature $\Delta \mathrm{T}$ is small and $\Delta \mathrm{R}=\left(\mathrm{R}-\mathrm{R}_{0}\right)<<\mathrm{R}_{0}$.
(1) Statement–1 is true, Statement–2 is true; Statement–2 is not the correct explanation of Statement–1
(2) Statement–1 is false, Statement–2 is true
(3) Statement–1 is true, Statement–2 is false
(4) Statement–1 is true, Statement–2 is true; Statement–2 is the correct explanation of Statement–1
[AIEEE - 2009]
Ans. (1)
Q. Two conductors have the same resistance at $0^{\circ} \mathrm{C}$ but their temperature coefficients of resistance are $\alpha_{1}$ and $\alpha_{2}$. The respective temperature coefficients of their series and parallel combinations are nearly :
(1) $\frac{\alpha_{1}+\alpha_{2}}{2}, \frac{\alpha_{1}+\alpha_{2}}{2}$
(2) $\frac{\alpha_{1}+\alpha_{2}}{2}, \alpha_{1}+\alpha_{2}$
(3) $\alpha_{1}+\alpha_{2}, \frac{\alpha_{1}+\alpha_{2}}{2}$
(4) $\alpha_{1}+\alpha_{2}, \frac{\alpha_{1} \alpha_{2}}{\alpha_{1}+\alpha_{2}}$
[AIEEE - 2010]
Ans. (1)
For series combination
$\alpha_{\mathrm{S}}=\frac{\alpha_{1} \mathrm{R}_{01}+\alpha_{2} \mathrm{R}_{02}}{\mathrm{R}_{01}+\mathrm{R}_{02}}$
$\mathrm{R}_{01}=\mathrm{R}_{02}=\mathrm{R}_{0}(\text { given })$
$\alpha_{\mathrm{S}}=\frac{\alpha_{1}+\alpha_{2}}{2}$
For parallel combination
$\frac{1}{\mathrm{R}}=\frac{1}{\mathrm{R}_{1}}+\frac{1}{\mathrm{R}_{2}}$
$\Rightarrow \frac{1}{\mathrm{R}_{e q}}=\frac{1}{\mathrm{R}_{0}\left(1+\alpha_{1} \mathrm{t}\right)}+\frac{1}{\mathrm{R}_{0}\left(1+\alpha_{2} \mathrm{t}\right)}$
$\frac{1}{\frac{\mathrm{R}_{0}}{2}\left(1+\alpha_{p} \mathrm{t}\right)}=\frac{1}{\mathrm{R}_{0}\left(1+\alpha_{1} \mathrm{t}\right)}+\frac{1}{\mathrm{R}_{0}\left(1+\alpha_{2} \mathrm{t}\right)}$
$2\left(1+\alpha_{p} t\right)^{-1}=\left(1+\alpha_{1} t\right)^{-1}+\left(1+\alpha_{2} t\right)^{-1}$
using binomial expansion
$2-2 \alpha_{\mathrm{p}} \mathrm{t}=1-\alpha_{1} \mathrm{t}+1-\alpha_{2} \mathrm{t} \Rightarrow \alpha_{\mathrm{p}}=\frac{\alpha_{1}+\alpha_{2}}{2}$
Q. If a wire is stretched to make it 0.1 % longer its resistance will :-
(1) decrease by 0.2%
(2) decrease by 0.05%
(3) increase by 0.05%
(4) increase by 0.2%
[AIEEE - 2011]
Ans. (4)
$\mathrm{R}=\rho \frac{\ell}{\mathrm{A}} \Rightarrow \mathrm{R} \alpha \ell^{2}$
$\frac{\Delta \mathrm{R}}{\mathrm{R}}=\frac{\Delta \mathrm{R}}{\mathrm{R}}=\frac{2 \Delta \ell}{\ell}=2[0.1]=0.2 \%$ increase.
Q. If $400 \Omega$ of resistance is made by adding four $100 \Omega$ resistance of tolerance 5%, then the tolerance of the combination is :
(1) 20% (2) 5% (3) 10% (4) 15%
[AIEEE - 2011]
Ans. (2)
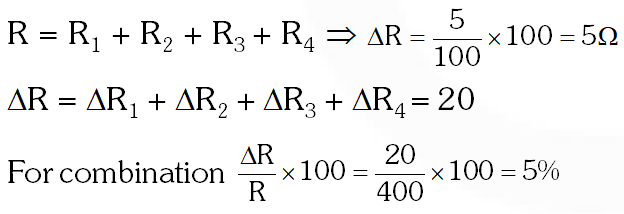
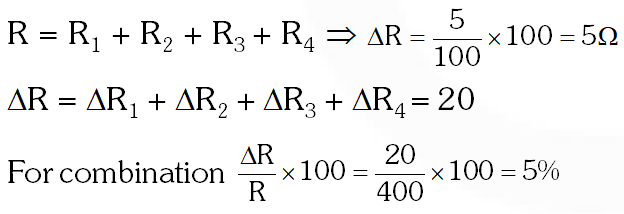
Q. The current in the primary circuit of a potentiometer is 0.2 A. The specific resistance and cross-section of the potentiometer wire are $4 \times 10^{-7}$ ohm metre and $8 \times 10^{-7} \mathrm{m}^{2}$ respectively. The potential gradient will be equal to :-
(1) 0.2 V/m (2) 1 V/m (3) 0.5 V/m (4) 0.1 V/m
[AIEEE - 2011]
Ans. (4)
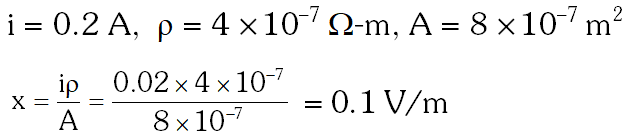
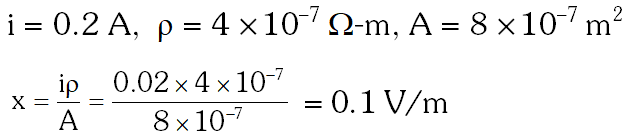
Q. Resistance of a given wire is obtained by measuring the current flowing in it and the voltage difference applied across it. If the percentage errors in the measurement of the current and the voltage difference are 3% each, then error in the value of resistance of the wire is :-
(1) 3% (2) 6% (3) zero (4) 1%
[AIEEE - 2012]
Ans. (2)
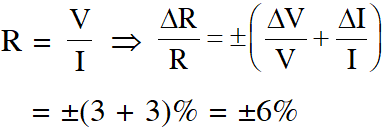
Q. Two electric bulbs marked 25W-220 V and 100 W-220 V are connected in series to a 440 V supply. Which of the bulbs will fuse ?
(1) Neither (2) Both (3) 100 W (4) 25 W
[AIEEE - 2012]
Ans. (4)
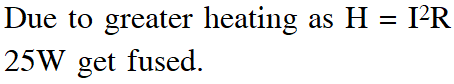
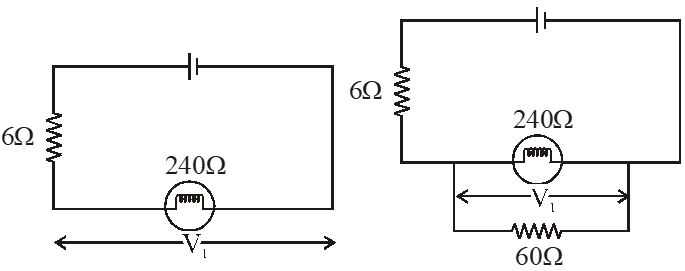
Q. The supply voltage to a room is 120V. The resistance of the lead wires is $6 \Omega$A 60 W bulb is already switched on. What is the decrease of voltage across the bulb, when a 240 W heater is switched on in parallel to the bulb?
(1) zero Volt (2) 2.9 Volt (3) 13.3 Volt (4) 10.04 Volt
[JEE-Mains 2013]
Ans. (4)
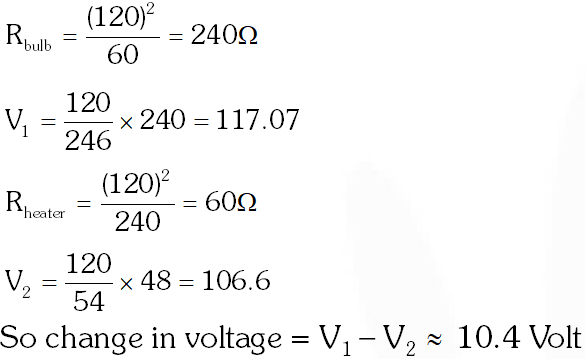
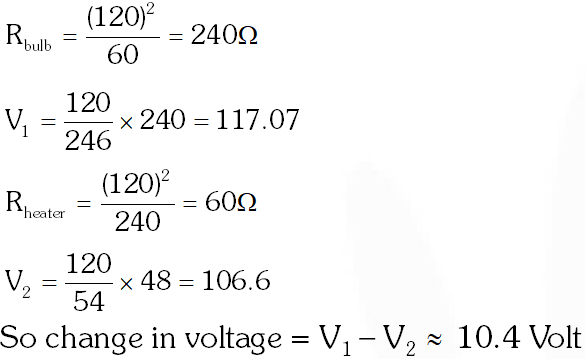
Q. This question has Statement I and Statement II. Of the four choice given after the Statements, choose the one that best describes the two Statements.
Statement-I : Higher the range, greater is the resistance of ammeter.
Statement-II : To increase the range of ammeter, additional shunt needs to be used across it.
(1) Statement-I is true, Statement-II is true, Statement-II is the correct explanation of Statement- I
(2) Statement-I is true, Statement-II is true, Statement-II is not the correct explanation of Statement- I.
(3) Statement-I is true, Statement-II is false.
(4) Statement-I is false, Statement-II is true.
[JEE-Mains 2013]
Ans. (4)
To increase the range of ammeter, resistance should be decreased (So additional shunt connected in parallel) so total resistance to ammeter decreases.
Q. In a large building, there are 15 bulbs of 40 W, 5 bulbs of 100 W, 5 fans of 80 W and 1 heater of 1 kW. The voltage of the electric mains is 220 V. The minimum capacity of the main fuse of the building will be :
(1) 12 A (2) 14 A (3) 8 A (4) 10 A
[JEE-Mains 2014]
Ans. (1)
All devices are in parallel so total current drawn is gives as
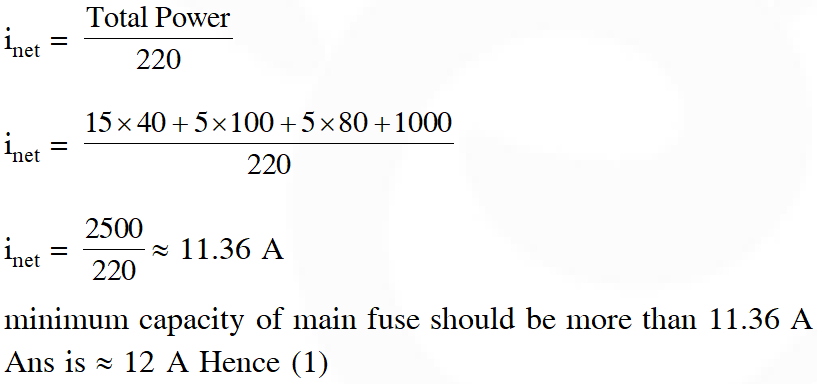
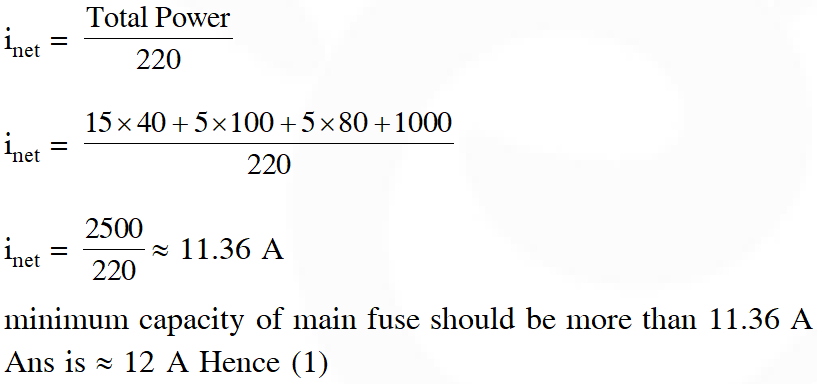
Q. When 5V potential difference is applied across a wire of length 0.1 m, the drift speed of electrons is $2.5 \times 10^{-4} \mathrm{ms}^{-1}$. If the electron density in the wire is $8 \times 10^{28} \mathrm{m}^{-3}$, the resistivity of the material is close to :-
(1) $1.6 \times 10^{-6} \Omega \mathrm{m}$
(2) $1.6 \times 10^{-5} \Omega \mathrm{m}$
(3) $1.6 \times 10^{-8} \Omega \mathrm{m}$
(4) $1.6 \times 10^{-7} \Omega \mathrm{m}$
[JEE-Mains 2015]
Ans. (2)
$\mathrm{V} \quad=\mathrm{i} \mathrm{R}=\left(\mathrm{neAV}_{\mathrm{d}}\right)\left(\frac{\rho \ell}{\mathrm{A}}\right)$
$\mathrm{V}=\mathrm{neV}_{\mathrm{d}} \ell$
$\rho=\frac{\mathrm{V}}{\mathrm{neV}_{\mathrm{d}} \ell}$
On putting values are got the answer
$=1.6 \times 10^{-5} \Omega \mathrm{m}$
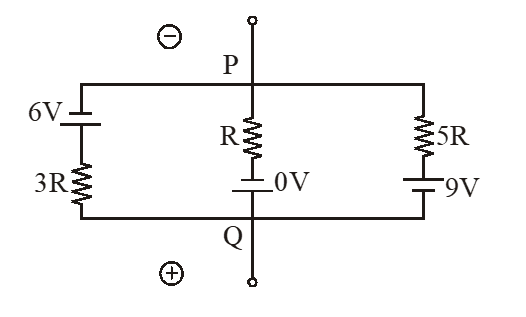
Q. In the circuit shown, the current in the $1 \Omega$ resistor is :-
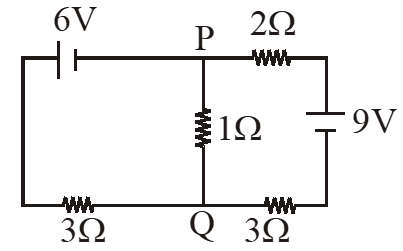(1) 0.13 A, from Q to P
(2) 0.13 A, from P to Q
(3) 1.3 A, from P to Q
(4) 0A
[JEE-Mains 2015]
(1) 0.13 A, from Q to P
(2) 0.13 A, from P to Q
(3) 1.3 A, from P to Q
(4) 0A
[JEE-Mains 2015]
Ans. (1)
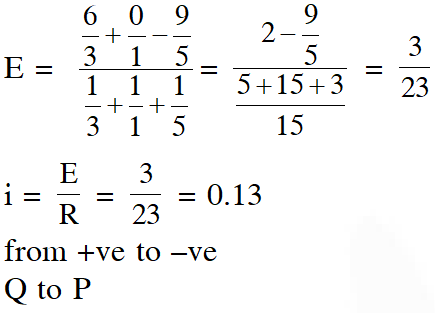
Q. A galvanometer having a coil resistance of $100 \Omega$ gives a full scale deflection, when a current of 1 mA is passed through it. The value of the resistance, which can convert this galvanometer into ammeter giving a full scale deflection for a current of 10A, is :-
(1) $3 \Omega$
(2) $0.01 \Omega$
(3) $2 \Omega$
(4) $0.1 \Omega$
[JEE-Mains 2016]
Ans. (2)
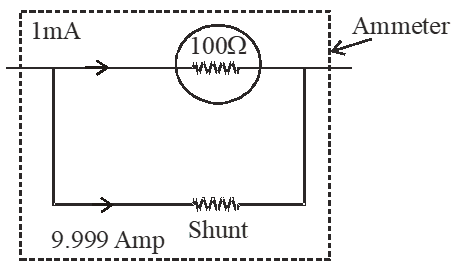
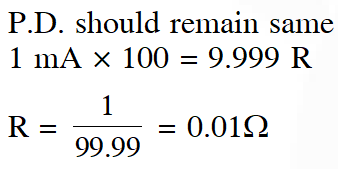
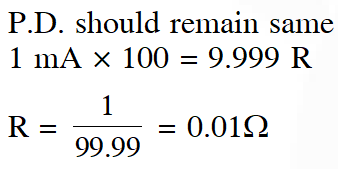
Q. Which of the following statements is false ?
(1) A rheostat can be used as a potential divider
(2) Kirchhoff's second law represents energy conservation
(3) Wheatstone bridge is the most sensitive when all the four resistances are of the same order
of magnitude.
(4) In a balanced wheatstone bridge if the cell and the galvanometer are exchanged, the point is disturbed.
[JEE-Mains 2017]
Ans. (4)
On interchanging Cell & Galvanometer.
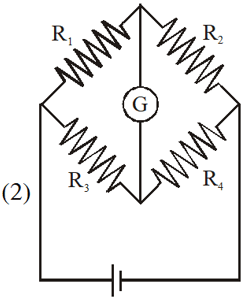On balancing condition
$\frac{\mathrm{R}_{1}}{\mathrm{R}_{3}}=\frac{\mathrm{R}_{2}}{\mathrm{R}_{4}}$ ....(1)
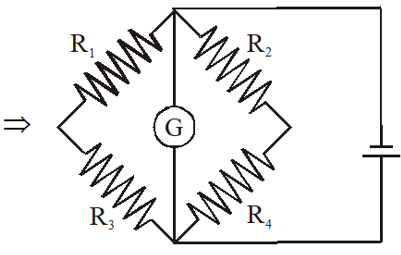
On interchanging Cell & Galvanometer.
On balancing condition
$\frac{\mathrm{R}_{1}}{\mathrm{R}_{3}}=\frac{\mathrm{R}_{2}}{\mathrm{R}_{4}}$ ....(1)
Q. When a current of 5 mA is passed through a galvanometer having a coil of resistance $15 \Omega$, it shows full scale deflection. The value of the resistance to be put in series with the galvanometer to convert it into to voltmeter of range 0 – 10 V is :-
(1) $2.535 \times 10^{3} \Omega$
(2) $4.005 \times 10^{3} \Omega$
(3) $1.985 \times 10^{3} \Omega$
(4) $2.045 \times 10^{3} \Omega$
[JEE-Mains 2017]
Ans. (3)
$10=\left(5 \times 10^{-3}\right)(15+\mathrm{R})$
$r=1985 \Omega$
Q. In the above circuit the current in each resistance is :-
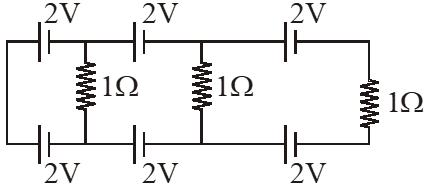(1) 0.5 A (2) 0 A (3) 1 A (4) 0.25 A
[JEE-Mains 2017]
(1) 0.5 A (2) 0 A (3) 1 A (4) 0.25 A
[JEE-Mains 2017]
Ans. (2)
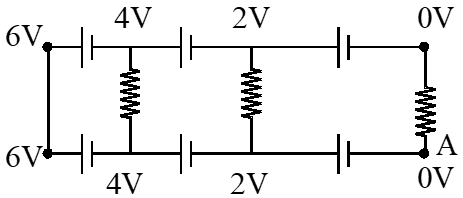Taking voltage of point A as = 0
Then voltage at other points can be written as shown in figure
Hence voltage across all resistance is zero.
Hence current = 0
Taking voltage of point A as = 0
Then voltage at other points can be written as shown in figure
Hence voltage across all resistance is zero.
Hence current = 0
Q. In a potentiometer experiment, it is found that no current passes through the galvanometer when the terminals of the cell are connected across 52 cm of the potentiometer wire. If the cell is shunted by a resistance of $5 \Omega$, a balance is found when the cell is connected across40 cm of the wire. Find the internal resistance of the cell.
(1) $1.5 \Omega$
(2) $2 \Omega$
(3) $2.5 \Omega$
(4) 1 $\Omega$
[JEE-Mains 2018]
Ans. (1)
without shunting condition :
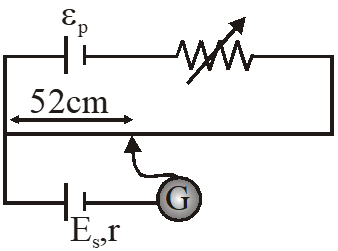
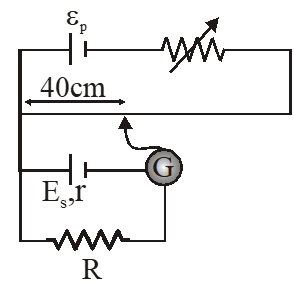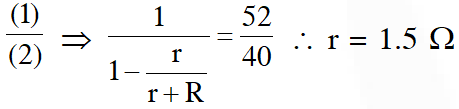
On balancing
$\mathrm{E}_{\mathrm{s}}-\frac{\mathrm{E}_{\mathrm{s}}}{(\mathrm{r}+\mathrm{R})} \mathrm{r}=40 \times \mathrm{x} \quad \ldots .(2)$
On solving :
On balancing
$\mathrm{E}_{\mathrm{s}}-\frac{\mathrm{E}_{\mathrm{s}}}{(\mathrm{r}+\mathrm{R})} \mathrm{r}=40 \times \mathrm{x} \quad \ldots .(2)$
On solving :
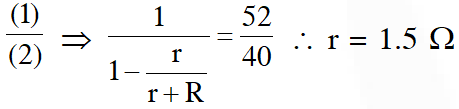
Q. On interchanging the resistances, the balance point of a meter bridge shifts to the left by 10 cm. The resistance of their series combination is 1 $\mathrm{k} \Omega$. How much was the resistance on the left slot before interchanging the resistances ?
(1) $505 \mathrm{k\Omega}$
(2) $550 \mathrm{k} \Omega$
(3) $910 \mathrm{k} \Omega$
(4) $990 \mathrm{k} \Omega$
[JEE-Mains 2018]
Ans. (2)
$\mathrm{R}_{1}+\mathrm{R}_{2}=1000 \Rightarrow \mathrm{R}_{2}=1000-\mathrm{R}_{1}$
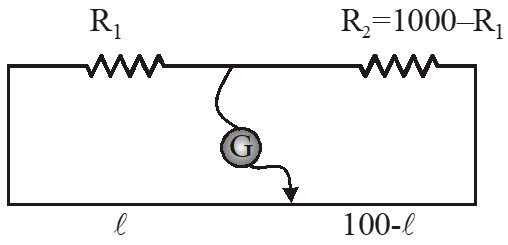On balancing condition
$\mathrm{R}_{1}(100-\ell)=\left(1000-\mathrm{R}_{1}\right) \ell \quad \ldots(1)$
On Inter changing resistance
On balancing condition
On balancing condition
$\mathrm{R}_{1}(100-\ell)=\left(1000-\mathrm{R}_{1}\right) \ell \quad \ldots(1)$
On Inter changing resistance
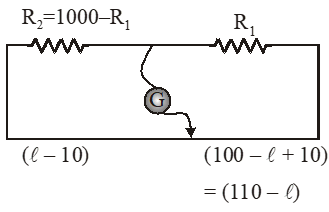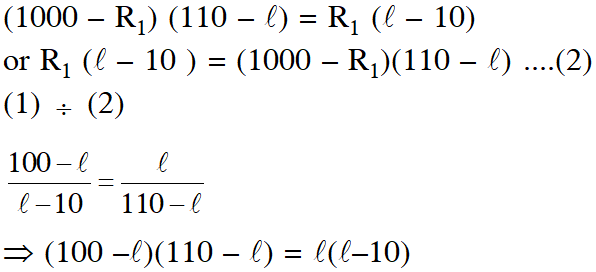
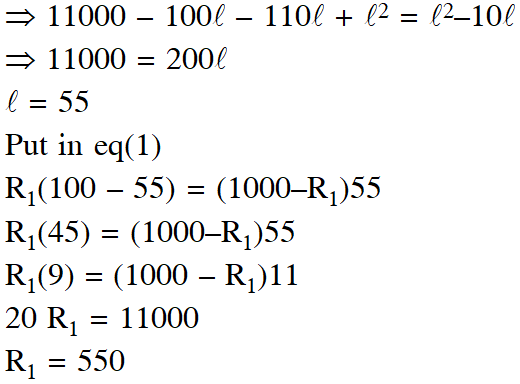
On balancing condition
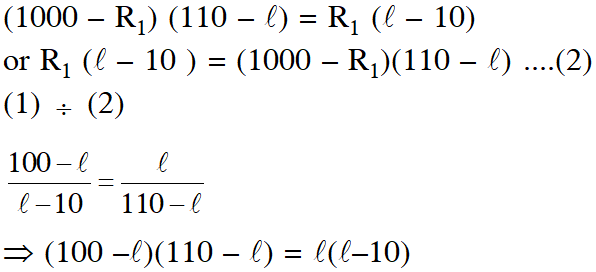
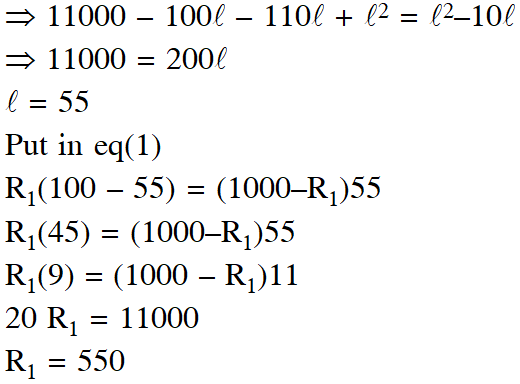
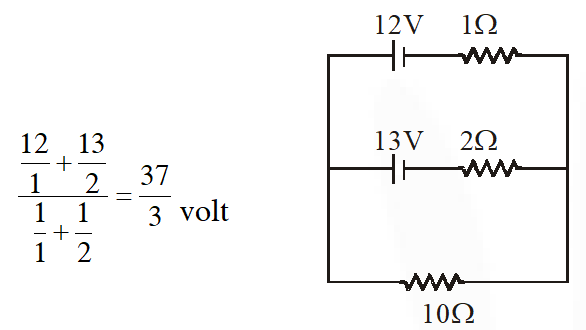
Q. Two batteries with e.m.f 12 V and 13 V are connected in parallel across a load resistor of $10 \Omega$. The internal resistances of the two batteries are $10 \Omega$ and $2 \Omega$respectively. The voltage across the load lies between002E
(1) 11.5 V and 11.6 V
(2) 11.4 V and 11.5 V
(3) 11.7 V and 11.8 V
(4) 11.6 V and 11.7 V
[JEE-Mains 2018]
Ans. (1)
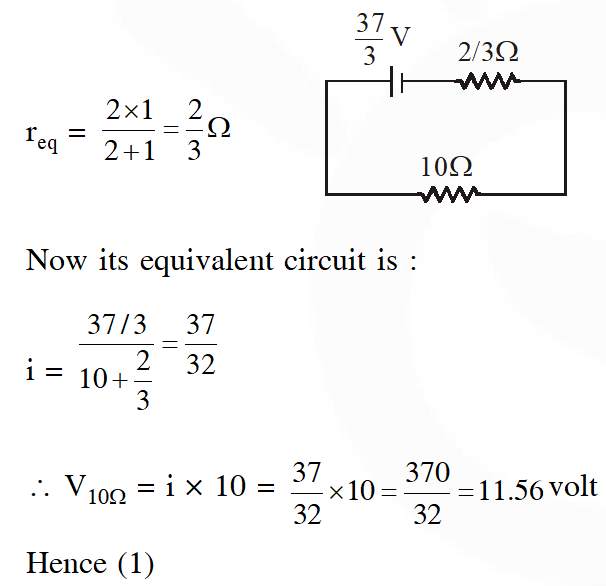
Comments
Kirti
May 8, 2021, 4:22 p.m.
In last question.. voltage should be 11.6 volt 🧐 because it is 11.56 and rounding off it we'll get 11.6 I think 🤔
Kirti Tripathi
May 8, 2021, 4:21 p.m.
In last question.. voltage should be 11.6 volt 🧐 because it is 11.56 and rounding off it we'll get 11.6 I think 🤔
R.shilpa
Jan. 29, 2021, 8:29 p.m.
it was a very interesting problems i enjoy it it was very easy to solve for me .tq for sending and giving deep explanation to this problems . i liked this problems by this problems i improve how to attempt tricks to solve the problems
R.shilpa
Jan. 29, 2021, 8:27 p.m.
it was a very interesting problems i enjoy it it was very easy to solve for me .tq for sending and giving deep explanation to this problems . i liked this problems
Rohit PUBG
Aug. 22, 2020, 6:08 p.m.
Thank you so much sir 🙏🙏🙏
Thanks for your previous year JEE main question paper and solution all solution are are step wise and easy to understand
All the best Saransh sir Jay esarl Jay physics
Anupavani
Aug. 18, 2020, 12:40 p.m.
So Nice I really learned so much....A biggest Thank you for Saral.........
mr nobody
July 29, 2020, 10:08 p.m.
in the last question, the values for the internal resistances are wrong. different values are used in the solution.
Narasimha Reddy Boggula
July 17, 2020, 12:25 a.m.
Excellent problems and for my side one request that is please keep more problems