Difference between Velocity and Acceleration
JEE Mains & Advanced (1) (1).jpeg)
Let's understand the difference between velocity and acceleration are two key concepts in the study of physics and mechanics. They are closely related, but they have distinct differences.
Difference between Velocity and Acceleration
| Velocity | Acceleration |
| It alludes to the speed of an object in a given direction. | Acceleration implies any change in the velocity of an object with respect to time |
| It is calculated with displacement | It is calculated with the velocity |
| Vector in nature | Vector in nature |
| It is rate of change of displacement | It is rate of Change of Velocity |
| Formula-Displacement/Time (d/t) | Formula- Change in velocity/Time (v/t) |
| It ascertains how fast is an object moving, and in which direction? | It ascertains how fast an object’s velocity changes with time? |
| Unit of measurement-meter/second (m/s) | Unit of measurement-meter/second2 (m/s2) |
Importance of understanding both the concepts.
Understanding both concepts are important for a number of reasons:
- Physics: Both are fundamental concepts in the study of physics, particularly in mechanics and kinematics. Understanding these concepts is crucial for a deeper understanding of physical phenomena such as motion, forces, and energy.
- Engineering: Engineers use both in various fields, including aerospace, mechanical, and civil engineering. For example, in aerodynamics, understanding both is important for the design of aircraft and their flight performance.
- Everyday life: both are relevant to everyday experiences and activities. For example, you can use a person's acceleration and velocity to calculate the time required to travel a specific distance or the force involved in a collision.
- Problem-solving: The ability to apply both concepts is important in solving problems in various fields, such as physics, engineering, and mathematics.
In conclusion, understandingn both concepts are important for a deeper understanding of physical phenomena, technology, and everyday life, as well as for problem-solving and career development in various fields.
Definition of velocity
Velocity is a measure of an object's speed and direction of motion. It is a vector quantity, meaning it has both a magnitude (the speed) and a direction. For example, an object moving at a constant speed of 30 meters per second (m/s) in a straight line would have a velocity of 30 m/s. If the object were to change direction, its velocity would change to reflect the new direction.
Velocity as a vector quantity
It is a vector quantity, which means it has both magnitude and direction. The magnitude of it represents the speed of an object, while the direction represents the direction of motion. Vector quantities are different from scalar quantities, which only have magnitude and no direction.
For example, consider a car driving on a road at a constant speed of 60 miles per hour in the east direction. The magnitude of the velocity is 60 miles per hour, which represents the speed of the car, while the direction is east, which represents the direction of motion.
Vector quantities can be added and subtracted, and their operations follow the rules of vector arithmetic. This means that the magnitude and direction of the velocity of an object can be changed by adding or subtracting velocities or accelerations.
In summary, It is a vector quantity that represents the speed and direction of an object's motion. It has both magnitude and direction, with the magnitude representing the speed and the direction representing the direction of motion.
Formula of velocity as the rate of change of displacement over time
It is calculated as the rate of change of an object's displacement over time. Displacement is a vector quantity that represents the change in position of an object and is defined as the final position minus the initial position. The velocity of an object can be calculated using the following formula:
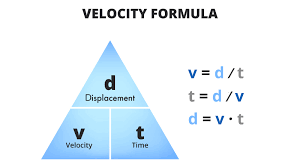
v = Δd / Δt
where v is the velocity, Δd is the change in displacement (final displacement minus initial displacement), and Δt is the change in time.
For example, consider a car that moves from position A to position B in a time interval of 10 seconds. If the displacement of the car from position A to position B is 100 meters, then the velocity of the car can be calculated as follows:
v = Δd / Δt = (100 m - 0 m) / (10 s - 0 s) = 10 m/s
In this example, the velocity of the car is 10 meters per second in the direction from position A to position B.
In summary, velocity is calculated as the rate of change of displacement over time. It is represented by the formula v = Δd / Δt, where v is the velocity, Δd is the change in displacement, and Δt is the change in time.
Definition of Acceleration
It is a measure of how an object's velocity changes over time. It is also a vector quantity and is typically measured in meters per second squared (m/s^2). An object is said to be accelerating if its velocity is changing, whether that change is in speed, direction or both. For example, if an object starts from rest and accelerates to a speed of 60 m/s over a period of 5 seconds, its acceleration would be 12 m/s^2.
Acceleration as a vector quantity
It is a vector quantity, meaning it has both magnitude and direction. The magnitude of it represents the rate of change of velocity, while the direction of it represents the direction of change of velocity. For example, if an object is moving in a straight line and its velocity is increasing, then the direction of acceleration is in the same direction as the velocity. If an object is moving in a straight line and its velocity is decreasing, then the direction of acceleration is in the opposite direction to the velocity.
It is also a vector quantity in the sense that it can have both positive and negative values. A positive value of acceleration means that the velocity of an object is increasing, while a negative value of acceleration means that the velocity of an object is decreasing. For example, if an object is moving in a straight line and its velocity is increasing, then the acceleration is positive. If an object is moving in a straight line and its velocity is decreasing, then the acceleration is negative.
In summary, It is a vector quantity that has both magnitude and direction. The magnitude of acceleration represents the rate of change of velocity, while the direction of acceleration represents the direction of change of velocity. Acceleration can have both positive and negative values, with positive acceleration meaning the velocity is increasing and negative acceleration meaning the velocity is decreasing.
Formula of acceleration as the rate of change of velocity over time
Acceleration can be calculated as the rate of change of velocity over time. Mathematically, acceleration is represented as the derivative of velocity with respect to time, or a = dv/dt, where a is the acceleration, dv is the change in velocity, and dt is the change in time.
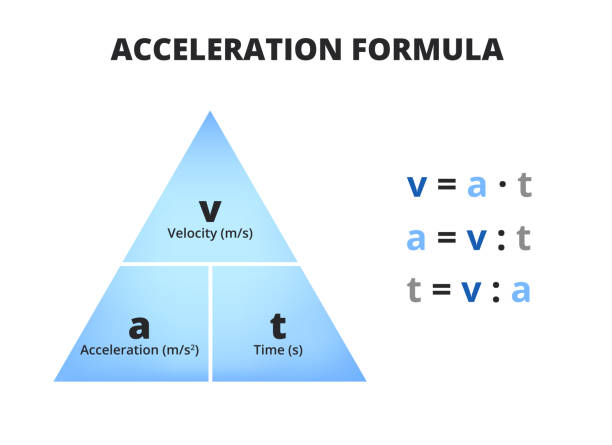
For example, consider an object moving with a velocity of 10 m/s that increases to a velocity of 20 m/s in a time interval of 5 seconds. The acceleration of the object
a = Δv / Δt = (20 m/s - 10 m/s) / (5 s - 0 s) = 2 m/s^2
In this example, the acceleration of the object is 2 m/s^2, which means that the velocity of the object is increasing by 2 m/s every second.
In summary, acceleration can be calculated as the rate of change of velocity over time using the formula a = dv/dt, where a is the acceleration, dv is the change in velocity, and dt is the change in time. This formula provides a quantitative measure of how the velocity of an object is changing over time.
Some practice numerical questions on vector and acceleration
- A car is traveling at a constant velocity of 60 km/hr. What is its acceleration?
Solution: Velocity is a vector quantity that represents the rate of change of an object's position. If an object is traveling at a constant velocity, its acceleration is zero. Hence, the acceleration of the car is 0 m/s².
- A car is moving with an acceleration of 2 m/s². What is its velocity after 5 seconds?
Solution: We can use the equation v = u + at, where v is the final velocity, u is the initial velocity (which is assumed to be 0), a is the acceleration and t is the time. Hence, v = 0 + (2 m/s² * 5 s) = 10 m/s.
- A ball is thrown vertically upward with an initial velocity of 10 m/s. What is its velocity after 2 seconds?
Solution: We can use the equation v = u + at, where v is the final velocity, u is the initial velocity, a is the acceleration (which is -9.8 m/s², due to gravity) and t is the time. Hence, v = 10 + (-9.8 m/s² * 2 s) = 1.6 m/s.
- An object is moving with a velocity of 8 m/s and has an acceleration of -2 m/s². What is its velocity after 3 seconds?
Solution: We can use the equation v = u + at, where v is the final velocity, u is the initial velocity, a is the acceleration and t is the time. Hence, v = 8 + (-2 m/s² * 3 s) = 2 m/s.
- A car is moving with an acceleration of 3 m/s². What is its velocity after 4 seconds if its initial velocity is 5 m/s?
Solution: We can use the equation v = u + at, where v is the final velocity, u is the initial velocity, a is the acceleration and t is the time. Hence, v = 5 + (3 m/s² * 4 s) = 17 m/s.
Practical Applications of both the concepts
Bot have many practical applications in fields such as physics, engineering, and medicine. Some of the most common applications include:
- Mechanics: In mechanics, both concepts are used to describe the motion of objects. For example, velocity is used to determine the speed and direction of an object, while acceleration is used to determine how the velocity of an object changes over time.
- Aerospace Engineering: In aerospace engineering, both concepts are used to describe the motion of spacecraft, satellites, and other objects in space. The concepts of these objects are used to determine their trajectory and to make necessary adjustments to their flight paths.
- Automotive Engineering: In automotive engineering, both concepts are used to design and test vehicles. For example, engineers use acceleration to determine the performance of a vehicle and to make necessary improvements.
- Medical Applications: In medicine ,both concepts are used to measure body movements and to diagnose certain medical conditions. For example, accelerometry is used to monitor the movements of patients with Parkinson's disease or other neurological conditions.
- Sports Science: In sports science, both concepts are used to study and improve athletic performance. For example, coaches use acceleration data to determine the explosiveness of an athlete's movements and to make necessary training adjustments.
These are just a few examples of the many practical applications of velocit. Both concepts play an important role in our understanding of motion and have many real-world uses.
Summary
Here are the key points regarding velocity and acceleration:
- Velocity is a measure of an object's speed and direction of motion, expressed as a vector quantity.
- Acceleration is a measure of how an object's velocity changes over time, expressed as a vector quantity.
- The relationship between both is crucial in understanding the motion of objects.
- Both have important implications in fields such as transportation, safety, sports, technology, and health.
- A comprehensive understanding of velocity and acceleration is vital for anyone studying physics and its real-life applications."
