JEE Main Previous Year Question of Math with Solutions are available at eSaral. Practicing JEE Main Previous Year Papers Questions of mathematics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Q. The differential equation which represents the family of curves $y=c_{1} e^{c_{2} x},$ where $c_{1}$ and $c_{2}$ are arbitrary constants, is :-
(1) yy" = y'
(2) $\mathrm{yy}^{\prime \prime}=\left(\mathrm{y}^{\prime}\right)^{2}$
(3) $y^{\prime}=y^{2}$
(4) $y^{\prime \prime}=y^{\prime} y$
[AIEEE-2009]
Ans. (2)
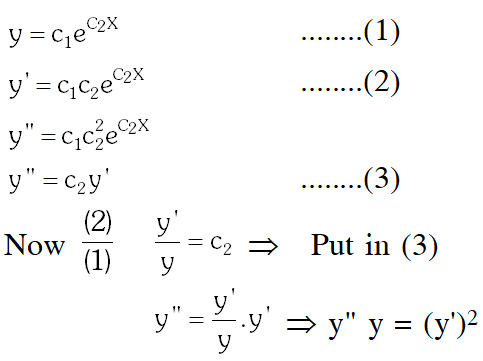
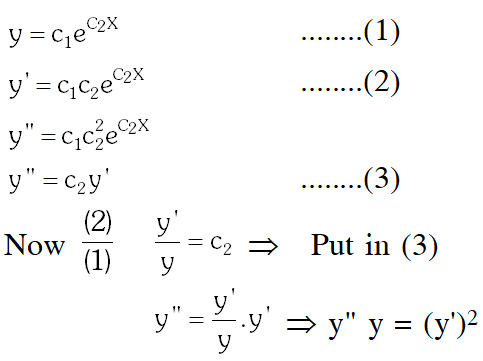
Q. Solution of the differential equation $\cos x$ dy $=y(\sin x-y) d x, 0
(1) sec x = (tan x + c) y
(2) y sec x = tan x + c
(3) y tan x = sec x + c
(4) tan x = (sec x + c) y
[AIEEE-2010]
Ans. (1)
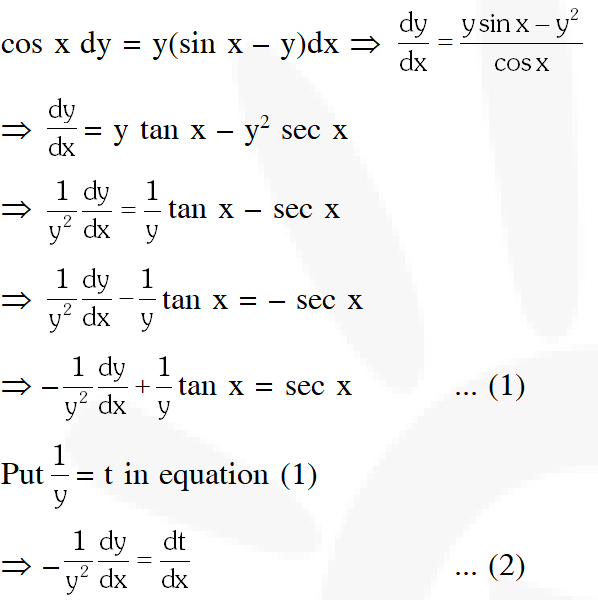
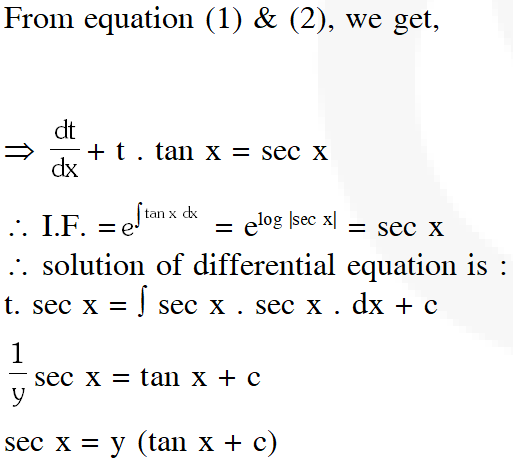
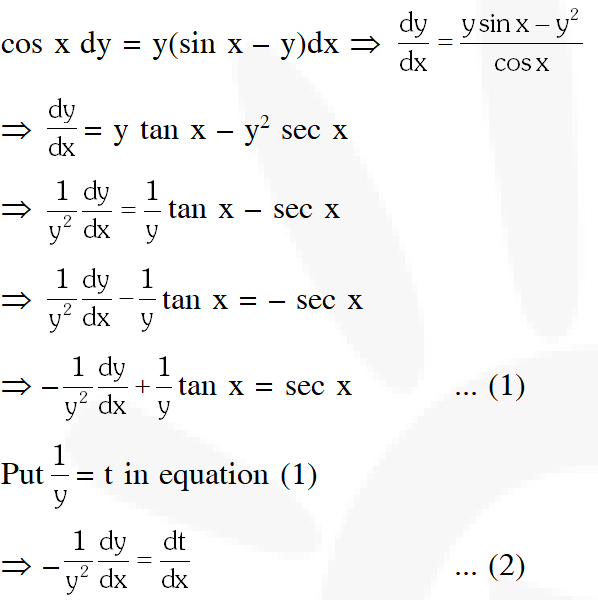
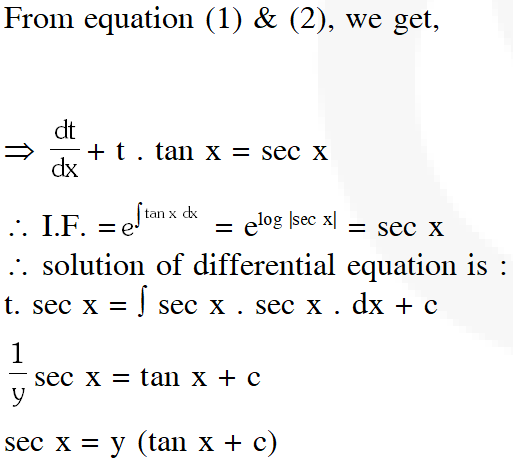
Q. If $\frac{d y}{d x}=y+3>0$ and $y(0)=2,$ then $y(\ln 2)$ is equal to $:-$
(1) 13 (2) –2 (3) 7 (4) 5
[AIEEE-2011]
Ans. (3)
$\frac{d y}{d x}=y+3>0 \quad y(0)=2, y(\log 2)=?$
$\int \frac{d y}{y+3}=\int d x$
$\log |y+3|=x+c$
$\mathrm{y}(0)=2$
$\log |2+3|=0+\mathrm{c} \Rightarrow \mathrm{c}=\log 5$
y. $(\log 2)=?$
$\log |y+3|=\log 2+\log 5$
$\log |y+3|=\log 10$
$y+3=10$
$y=7$
Q. Let I be the purchase value of an equipment and $V(t)$ be the value after it has been used for t years. The value $\mathrm{V}(\mathrm{t})$ depreciates at a rate given by differential equation $\frac{\mathrm{dV}(\mathrm{t})}{\mathrm{dt}}=-\mathrm{k}(\mathrm{T}-\mathrm{t})$ where $\mathrm{k}>0$ is a constant and $\mathrm{T}$ is the total life in years of the equipment. Then the scrap value $\mathrm{V}(\mathrm{T})$ of the equipment is :-.
(1) $\mathrm{I}-\frac{\mathrm{k}(\mathrm{T}-\mathrm{t})^{2}}{2}$
(2) $\mathrm{e}^{-\mathrm{kT}}$
(3) $\mathrm{T}^{2}-\frac{\mathrm{I}}{\mathrm{k}}$
(4) $\mathrm{I}-\frac{\mathrm{k} \mathrm{T}^{2}}{2}$
[AIEEE-2011]
Ans. (4)
$\frac{\mathrm{d} \mathrm{V}}{\mathrm{dt}}=-\mathrm{k}(\mathrm{T}-\mathrm{t})$
$\int \mathrm{d} \mathrm{V}=\int-\mathrm{k}(\mathrm{T}-\mathrm{t}) \mathrm{dt}$
$V=-k\left[T t-\frac{t^{2}}{2}\right]+C$
At $\mathrm{t}=0 \quad \mathrm{V}=\mathrm{I} \Rightarrow \mathrm{C}=\mathrm{I}$
$\mathrm{V}=-\mathrm{kt}\left(\mathrm{T}-\frac{\mathrm{t}}{2}\right)+\mathrm{I}$
$V(T)=-k T\left(T-\frac{T}{2}\right)+I=\frac{-k T^{2}}{2}+I$
Q. The curve that passes through the point (2, 3), and has the property that the segment of any tangent to it lying between the coordinate axes is bisected by the point of contact, is given by :
(1) $\left(\frac{x}{2}\right)^{2}+\left(\frac{y}{3}\right)^{2}=2$
(2) 2y – 3x = 0
(3) $y=\frac{6}{x}$
(4) $x^{2}+y^{2}=13$
[AIEEE-2011]
Ans. (3)
Equation of tangent at $\left(\mathrm{x}_{1}, \mathrm{y}_{1}\right)$ is
$y-y_{1}=\frac{d y_{1}}{d x_{1}}\left(x-x_{1}\right)$
$\mathrm{x}-$ intercept $=\mathrm{x}_{1}-\mathrm{y}_{1} \frac{\mathrm{d} \mathrm{x}_{1}}{\mathrm{d} y_{1}}$
According to question
$x_{1}=\frac{x_{1}-y_{1} \frac{d x_{1}}{d y_{1}}}{2}$
$\Rightarrow \mathrm{x}_{1}=-\mathrm{y}_{1} \frac{\mathrm{d} \mathrm{x}_{1}}{\mathrm{d} y_{1}}$
$\int \frac{d y}{y}=\int-\frac{d x}{x}$
$\Rightarrow \quad \ell n y=-\ell n x+\ell n c$
$\Rightarrow \quad \mathrm{y}=\frac{\mathrm{c}}{\mathrm{x}} \quad \Rightarrow \quad \mathrm{xy}=\mathrm{c}$
Now at $x=2, y=3$
$\Rightarrow \quad c=6$
$\therefore \quad x y=6 \quad \Rightarrow \quad y=\frac{6}{x}$
Q. Consider the differential equation $\mathrm{y}^{2} \mathrm{d} \mathrm{x}+\left(\mathrm{x}-\frac{1}{\mathrm{y}}\right) \mathrm{d} \mathrm{y}=0 .$ It $\mathrm{y}(1)=1,$ then $\mathrm{x}$ is given by :
(1) $1-\frac{1}{y}+\frac{\frac{1}{e^{y}}}{e}$
(2) $4-\frac{2}{y}-\frac{\frac{1}{e^{y}}}{e}$
(3) $3-\frac{1}{y}+\frac{\frac{1}{e^{y}}}{e}$
(4) $1+\frac{1}{y}-\frac{\frac{1}{e^{y}}}{e}$
[AIEEE-2011]
Ans. (4)
$\mathrm{y}^{2} \mathrm{d} \mathrm{x}+\left(\mathrm{x}-\frac{1}{\mathrm{y}}\right) \mathrm{d} \mathrm{y}=0$
$\Rightarrow \quad \mathrm{y}^{2} \frac{\mathrm{d} \mathrm{x}}{\mathrm{d} y}+\mathrm{x}=\frac{1}{\mathrm{y}} \quad \Rightarrow \quad \frac{\mathrm{d} \mathrm{x}}{\mathrm{d} y}+\frac{\mathrm{x}}{\mathrm{y}^{2}}=\frac{1}{\mathrm{y}^{3}}$
Integrating factor (I.F.) $=\mathrm{e}^{\int \frac{1}{\mathrm{y}^{2}} \mathrm{d} \mathrm{y}}=\mathrm{e}^{-1 / \mathrm{y}}$
General solution is -
\[ \mathbf{x} \cdot \mathrm{e}^{-1 / \mathrm{y}}=\int \frac{1}{y^{3}} e^{-1 / y} \mathrm{d} y+c \]
Let $\mathrm{I}_{1}=\int \frac{1}{y^{3}} e^{-1 / y} \mathrm{d} y$
put $\quad \frac{-1}{y}=t$
$y^{-2} d y=d t$
$\therefore \quad \mathrm{I}_{1}=-\int \mathrm{te}^{\mathrm{t}} \mathrm{dt}$
$=-e^{t}(t-1)$
$=e^{t}(1-t)$
General solution is
$\mathrm{xe}^{-1 / \mathrm{y}}=\mathrm{e}^{-1 / \mathrm{y}}\left(1+\frac{1}{\mathrm{y}}\right)+\mathrm{C}$
$\Rightarrow \quad \mathrm{x}=1+\frac{1}{y}+\mathrm{Ce}^{1 / \mathrm{y}}$
Put x = 1, y = 1
$\therefore \quad 1=1+\frac{1}{1}+\mathrm{Ce}^{1 / 1}$
$\Rightarrow \quad C=-1 / \mathrm{e}$
$\therefore \quad x=1+\frac{1}{y}-\frac{e^{1 / y}}{e}$
Q. The population p(t) at time t of a certain mouse species satisfies the differential equation $\mathrm{dp}(\mathrm{t})$ $\mathrm{dt}$ = 0.5 p(t) – 450. If p(0) = 850, then the time at which the population becomes zero is :
(1) ln18 (2) 2 ln18 (3) ln9 (4) $\frac{1}{2} \ln 18$
[AIEEE-2012]
Ans. (2)
$\frac{\mathrm{dp}(\mathrm{t})}{\mathrm{dt}}=\frac{1}{2} \mathrm{p}(\mathrm{t})-450$
integrate
$\int \frac{\mathrm{d} \mathrm{p}}{\mathrm{p}-900}=\int \frac{1}{2} \mathrm{d} \mathrm{t}$
$\ell \mathrm{n}|(\mathrm{p}-900)|=\frac{1}{2} \mathrm{t}+\mathrm{C} \quad \ldots .(1)$
given $\mathrm{t}=0 \rightarrow \mathrm{p}=850 \quad \therefore \mathrm{C}=\ell \mathrm{n} 50$
from ( 1)
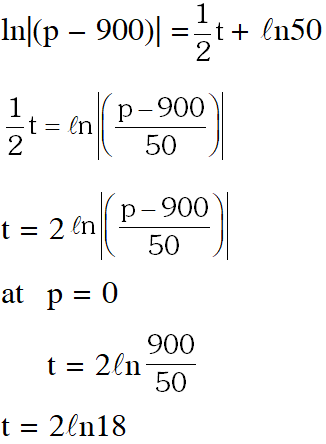
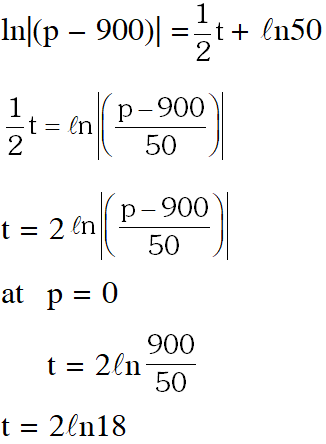
Q. At present a firm is manufacturing 2000 items. It is estimated that the rate of change of
production P w.r.t. additional number of workers x is given by $\frac{d P}{d x}=100-12 \sqrt{x}$. If the firm employs 25 more workers, then the new level of production of items is :
(1) 2500 (2) 3000 (3) 3500 (4) 4500
[JEE (Main)-2013]
Ans. (3)
$\mathrm{P}=100 \mathrm{x}-12 \mathrm{x}^{3 / 2} \cdot \frac{2}{3}+\mathrm{C}$
x = 0,
P = 2000
C = 2000
$\mathrm{P}_{(\mathrm{x}=25)}=2500-1000+2000=3500$
Q. If the surface area of a sphere of radius r is increasing uniformly at the rate $8 \mathrm{cm}^{2} / \mathrm{s}$, then the rate of change of its volume is :
(1) proportional to $r^{2}$
(2) constant
(3) proportional to r
(4) proportional to $\sqrt{\mathrm{r}}$
[JEE-Main (On line)-2013]
Ans. (3)
$\mathrm{S}=4 \pi \mathrm{r}^{2}$
$\frac{\mathrm{ds}}{\mathrm{dt}}=8=8 \pi \mathrm{r} \frac{\mathrm{dr}}{\mathrm{dt}} \& \quad \mathrm{v}=\frac{4}{3} \pi \mathrm{r}^{3}$
$\Rightarrow \frac{\mathrm{dv}}{\mathrm{dt}}=4 \pi \mathrm{r}^{2} \frac{\mathrm{dr}}{\mathrm{dt}}$
$\Rightarrow \frac{\mathrm{d} \mathrm{v}}{\mathrm{dt}}=4 \mathrm{r}$
Q. Consider the differential equation $\frac{\mathrm{d} y}{\mathrm{dx}}=\frac{\mathrm{y}^{3}}{2\left(\mathrm{xy}^{2}-\mathrm{x}^{2}\right)}$
Statement 1 : The substitution z $=y^{2}$ transforms the above equation into a first order homogenous differential equation.
Statement 2 : The solution of this differential equation is $y^{2} e^{-\frac{y^{2}}{x}}=C$.
(1) Statement 1 is false and statement 2 is true. (2) Both statements are true.
(3) Statement 1 is true and statement 2 is false. (4) Both statements are false.
[JEE-Main (On line)-2013]
Ans. (2)
put $z=y^{2}$
$\Rightarrow \quad \frac{\mathrm{d} z}{\mathrm{dx}}=2 \mathrm{y} \frac{\mathrm{d} \mathrm{y}}{\mathrm{d} \mathrm{x}}$
$\Rightarrow \quad$ D.E. is $\frac{\mathrm{d} z}{\mathrm{dx}}=\frac{2 \mathrm{z}^{2}}{2\left(\mathrm{xz}-\mathrm{x}^{2}\right)}$
$\Rightarrow \quad z(x d z-z d x)=x^{2} d z$
$\Rightarrow \quad \int d\left(\frac{z}{x}\right)=\int \frac{d z}{z}$
$\Rightarrow \quad \frac{\mathrm{z}}{\mathrm{x}}=\ell \mathrm{nz}+\ell \mathrm{nC}$
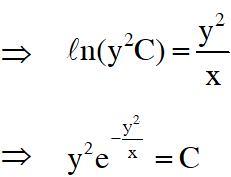
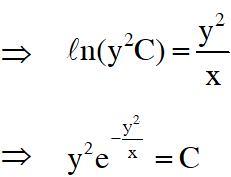
Q. If a curve passes through the point $\left(2, \frac{7}{2}\right)$ and has slope $\left(1-\frac{1}{\mathrm{x}^{2}}\right)$ at any point $(\mathrm{x}, \mathrm{y})$ on it, then the ordinate of the point on the curve whose abscissa is $-2$ is :
$(1)-\frac{5}{2}$
( 2)$\frac{5}{2}$
$(3)-\frac{3}{2}$
( 4)$\frac{3}{2}$
[JEE-Main (On line)-2013]
Ans. (3)
$\frac{\mathrm{d} y}{\mathrm{dx}}=1-\frac{1}{\mathrm{x}^{2}}$
$\Rightarrow \quad \mathrm{y}=\mathrm{x}+\frac{1}{\mathrm{x}}+1$
$\Rightarrow \quad \mathrm{y}=-2-\frac{1}{2}+1=-\frac{3}{2}$
Q. The equation of the curve passing through the origin and satisfying the differential equation $\left(1+x^{2}\right) \frac{d y}{d x}+2 x y=4 x^{2}$ is :
$(1)\left(1+x^{2}\right) y=x^{3}$
(2) $3\left(1+x^{2}\right) y=4 x^{3}$
(3) $3\left(1+x^{2}\right) y=2 x^{3}$
(4) $\left(1+x^{2}\right) y=3 x^{3}$
[JEE-Main (On line)-2013]
Ans. (2)
$\int \mathrm{d}\left(\left(1+\mathrm{x}^{2}\right) \mathrm{y}\right)=\int 4 \mathrm{x}^{2} \mathrm{d} \mathrm{x}$
$\Rightarrow \quad \mathrm{y}\left(1+\mathrm{x}^{2}\right)=\frac{4 \mathrm{x}^{3}}{3}+\mathrm{C}$ passes through $(0,0)$
$\Rightarrow \quad 3 \mathrm{y}\left(1+\mathrm{x}^{2}\right)=4 \mathrm{x}^{3}$
Q. Let the population of rabbits surviving at a time t be governed by the differential equation $\frac{\mathrm{dp}(\mathrm{t})}{\mathrm{dt}}=\frac{1}{2} \mathrm{p}(\mathrm{t})-200 .$ If $\mathrm{p}(0)=100,$ then $\mathrm{p}(\mathrm{t})$ equals :
(1) $400-300 \mathrm{e}^{\mathrm{t} / 2}$
(2) $300-200 \mathrm{e}^{-t / 2}$
(3) $600-500 \mathrm{e}^{t / 2}$
(4) $400-300 \mathrm{e}^{-1 / 2}$
[JEE(Main)-2014]
Ans. (1)
$\frac{\mathrm{dp}(\mathrm{t})}{\mathrm{dt}}=\frac{1}{2} \mathrm{p}(\mathrm{t})-200$
$\int_{10}^{p(t)} \frac{d p(t)}{p(t)-400}=\int_{0}^{t} \frac{d t}{2} \Rightarrow \log \left|\frac{p(t)-400}{-300}\right|=\frac{t}{2}$
$|p(t)-400|=300 e^{t / 2}$
$400-p(t)=300 e^{t / 2}$
$\therefore \mathrm{p}(\mathrm{t})=400-300 \mathrm{e}^{\mathrm{t} / 2}$
Q. Let $\mathrm{y}(\mathrm{x})$ be the solution of the differential equation $(\mathrm{x} \log \mathrm{x}) \frac{\mathrm{d} \mathrm{y}}{\mathrm{dx}}+\mathrm{y}=2 \mathrm{x} \log \mathrm{x},(\mathrm{x} \geq 1)$ Then $\mathrm{y}(\mathrm{e})$ is equal to :
(1) 2 (2) 2e (3) e (4) 0
[JEE(Main)-2015]
Ans. (1)
$(x \log x) \frac{d y}{d x}+y=2 x \log x,(x \geq 1)$
$\Rightarrow \frac{d y}{d x}+\frac{y}{x \log x}=2$
I.F. $=e^{\int \frac{d x}{x \log x}}=e^{\log (\log x)}=\log x$
Solution is $y \log x=\int 2 \log x d x$
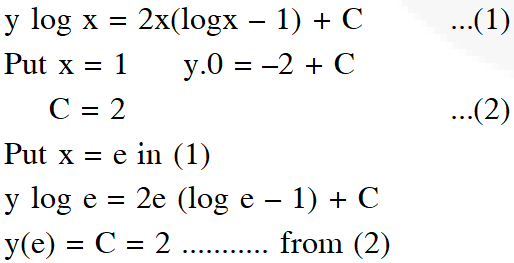
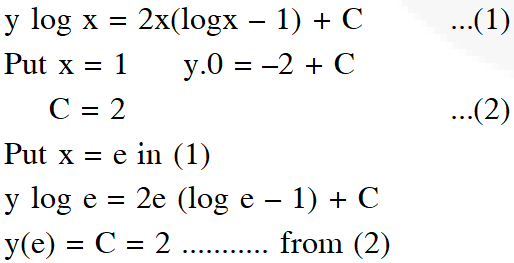
Q. If a curve $\mathrm{y}=\mathrm{f}(\mathrm{x})$ passes through the point $(1,-1)$ and satisfies the differential equation, $\mathrm{y}(1+\mathrm{xy}) \mathrm{dx}=\mathrm{x}$ dy, then $\mathrm{f}\left(-\frac{1}{2}\right)$ is equal to :
( 1)$\frac{4}{5}$
(2) $-\frac{2}{5}$
(3) $-\frac{4}{5}$
( 4)$\frac{2}{5}$
[JEE(Main)-2016]
Ans. (1)
Given differential equation
$\mathrm{ydx}+\mathrm{xy}^{2} \mathrm{dx}=\mathrm{xdy}$
$\Rightarrow \frac{\mathrm{xdy}-\mathrm{ydx}}{\mathrm{y}^{2}}=\mathrm{xdx}$
$\Rightarrow-\mathrm{d}\left(\frac{\mathrm{x}}{\mathrm{y}}\right)=\mathrm{d}\left(\frac{\mathrm{x}^{2}}{2}\right)$
Integrating we get
$-\frac{x}{y}=\frac{x^{2}}{2}+C$
$\because$ It passes through $(1,-1)$
$\therefore \quad 1=\frac{1}{2}+\mathrm{C} \Rightarrow \mathrm{C}=\frac{1}{2}$
$\therefore \quad x^{2}+1+\frac{2 x}{y}=0 \Rightarrow y=\frac{-2 x}{x^{2}+1}$
$\therefore \mathrm{f}\left(-\frac{1}{2}\right)=\frac{4}{5}$
Q. If $(2+\sin x) \frac{d y}{d x}+(y+1) \cos x=0$ and $y(0)=1,$ then $y\left(\frac{\pi}{2}\right)$ is equal to :-
(1) $\frac{4}{3}$
( 2)$\frac{1}{3}$
(3) $-\frac{2}{3}$
$(4)-\frac{1}{3}$
[JEE(Main)-2017]
Ans. (2)
$(2+\sin x) \frac{d y}{d x}+(y+1) \cos x=0$
$\frac{d}{d x}(2+\sin x)(y+1)=0$
$(2+\sin x)(y+1)=c$
$x=0, y=1 \Rightarrow c=4$
$\mathrm{y}+1=\frac{4}{2+\sin \mathrm{x}}$
$y\left(\frac{\pi}{2}\right)=\frac{4}{3}-1=\frac{1}{3}$
Q. Let $\mathrm{y}=\mathrm{y}(\mathrm{x})$ be the solution of the differential equation $\sin \mathrm{x} \frac{\mathrm{dy}}{\mathrm{dx}}+\mathrm{y} \cos \mathrm{x}=4 \mathrm{x}, \mathrm{x} \in(0$ \pi).
If $\mathrm{y}\left(\frac{\pi}{2}\right)=0,$ then $\mathrm{y}\left(\frac{\pi}{6}\right)$ is equal to :
(1) $\frac{-8}{9 \sqrt{3}} \pi^{2}$
(2) $-\frac{8}{9} \pi^{2}$
(3) $-\frac{4}{9} \pi^{2}$
(4) $\frac{4}{9 \sqrt{3}} \pi^{2}$
[JEE(Main)-2018]
Ans. (2)
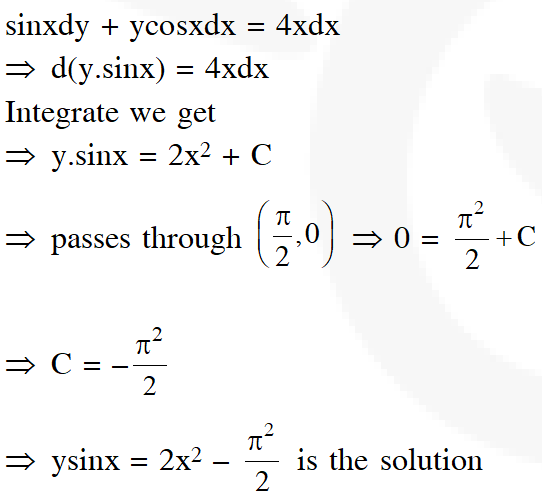
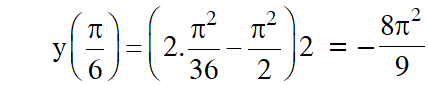
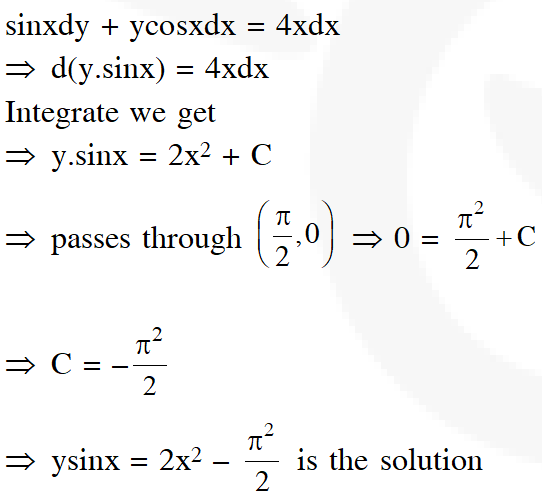
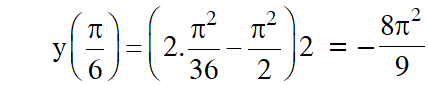
Comments
King sai rohit
Feb. 22, 2021, 4:27 p.m.
Well...it's very useful to those who are practicing at home!!!!
Shailesh gupta
Oct. 19, 2020, 7:14 p.m.
Please give sheet question in topic wise and write topic name for each every question🙋🙋🙋🙋🙋
