JEE Advanced Previous Year Questions of Physics with Solutions are available at eSaral. Practicing JEE Advanced Previous Year Papers Questions of Physics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
Get detailed Class 11th & 12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Click Here for JEE main Previous Year Topic Wise Questions of Physics with Solutions
Download eSaral app for free study material and video tutorials.
Simulator
Previous Years JEE Advanced Questions
Paragraph for Questions 8 and 9
A point charge Q is moving in a circular orbit of radius R in the x-y plane with an angular velocity $\omega$. This can be considered as equivalent to a loop carrying a steady current $\frac{\mathrm{Q} \omega}{2 \pi}$. A uniform magnetic field along the positive z-axis is now switched on, which increases at a constant rate from 0 to B in one second. Assume that the radius of the orbit remains constant. The application of the magnetic field induces an emf in the orbit. The induced emf is defined as the work done by an induced electric field in moving a unit positive charge around a closed loop. It is known that for an orbiting charge, the magnetic dipole moment is proportional to the angular momentum with a proportionality constant $\gamma$.
Q. The figure shows certain wire segments joined together to form a coplanar loop. The loop is placed in a perpendicular magnetic field in the direction going into the plane of the figure. The magnitude of the field increases with time. $\mathrm{I}_{1}$ and $\mathrm{I}_{2}$ are the currents in the segments ab and cd. Then,
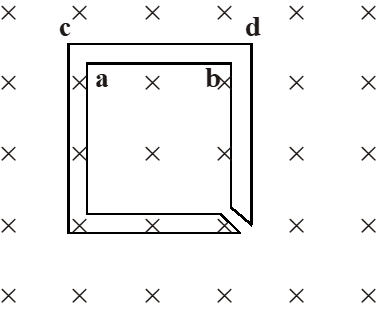(A) $\mathrm{I}_{1}>\mathrm{I}_{2}$
(B) $\mathrm{I}_{1}<\mathrm{I}_{2}$
(C) $\mathrm{I}_{1}$ is in the direction ba and $\mathrm{I}_{2}$ is in the direction $\mathrm{cd}$
(D) $\mathrm{I}_{1}$ is in the direction ab and $\mathrm{I}_{2}$ is in the direction de
[JEE-2009]
(A) $\mathrm{I}_{1}>\mathrm{I}_{2}$
(B) $\mathrm{I}_{1}<\mathrm{I}_{2}$
(C) $\mathrm{I}_{1}$ is in the direction ba and $\mathrm{I}_{2}$ is in the direction $\mathrm{cd}$
(D) $\mathrm{I}_{1}$ is in the direction ab and $\mathrm{I}_{2}$ is in the direction de
[JEE-2009]
Ans. (D)
As area of outer loop is bigger therefore emf induced in outer loop is dominant and therefore according to lenz law current in outer loop is Anticlockwise and inner loop is clockwise
Q. Two metallic rings A and B, identical in shape and size but having different resistivities $P_{\mathrm{A}}$ and $\rho_{\mathrm{B}}$, are kept on top of two identical solenoids as shown in the figure. When current I is switched on in both the solenoids in identical manner, the rings A and B jump to heights $\mathrm{h}_{\mathrm{A}}$ and $\mathrm{h}_{\mathrm{B}}$ respectively, with $\mathrm{h}_{\mathrm{A}}>\mathrm{h}_{\mathrm{B}}$. The possible relation(s) between their resistivities and their masses $\mathrm{m}_{\mathrm{A}}$ and $\mathrm{m}_{\mathrm{B}}$ is(are)
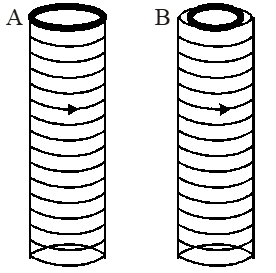
[JEE-2009]
[JEE-2009]
Ans. (B,D)
(a) when resistivity is low current induced will be more; therefore impulsive force on the ring will also be more and it jumps to higher levels. [But for this mass should be either less or equal to the other]
Q. A thin flexible wire of length L is connected to two adjacent fixed points and carries a current I in the clockwise direction, as shown in the figure. When the system is put in a uniform magnetic field of strength B going into the plane of the paper, the wire takes the shape of a circle. The tension in the wire is :-
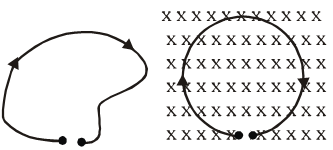(A) IBL
(B) $\frac{\mathrm{IBL}}{\pi}$
(C) $\frac{\mathrm{IBL}}{2 \pi}$
(D) $\frac{\mathrm{IBL}}{4 \pi}$
(A) IBL
(B) $\frac{\mathrm{IBL}}{\pi}$
(C) $\frac{\mathrm{IBL}}{2 \pi}$
(D) $\frac{\mathrm{IBL}}{4 \pi}$
Ans. (C)
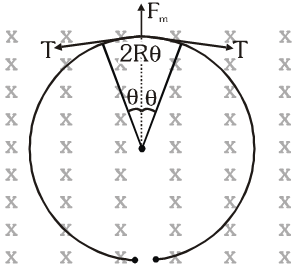$2 \mathrm{T} \sin \theta=\mathrm{IB}(2 \mathrm{R} \theta) .$ As $\theta$ is small so $\sin \theta \approx \theta$
$\Rightarrow 2 \mathrm{T}(\theta)=2 \mathrm{IBR} \theta \Rightarrow \mathrm{T}=\mathrm{BIR}=\frac{\mathrm{IBL}}{2 \pi} \quad[\because 2 \pi \mathrm{R}=\mathrm{L}]$
$2 \mathrm{T} \sin \theta=\mathrm{IB}(2 \mathrm{R} \theta) .$ As $\theta$ is small so $\sin \theta \approx \theta$
$\Rightarrow 2 \mathrm{T}(\theta)=2 \mathrm{IBR} \theta \Rightarrow \mathrm{T}=\mathrm{BIR}=\frac{\mathrm{IBL}}{2 \pi} \quad[\because 2 \pi \mathrm{R}=\mathrm{L}]$
Q. Which of the field patterns given below is valid for electric field as well as for magnetic field?
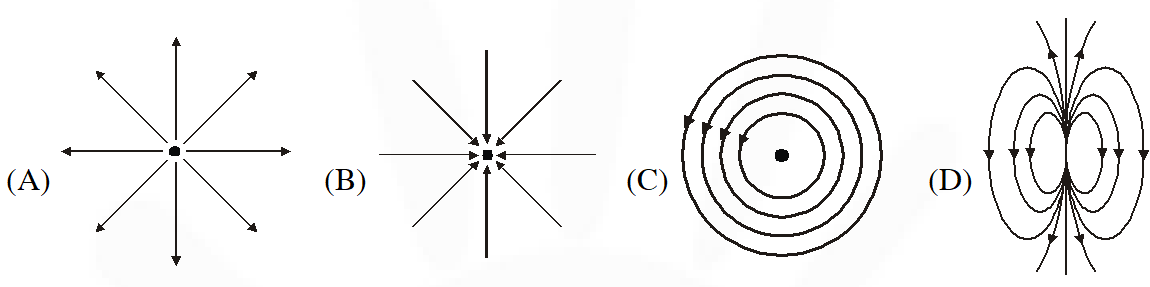[JEE 2011]
[JEE 2011]
Ans. (C)
Magnetic field lines and induced electric field lines always from closed loop.
Q. A long circular tube of length 10 m and radius 0.3 m carries a current I along its curved surface as shown. A wire-loop of resistance 0.005 ohm and of radius 0.1 m is placed inside the tube with its axis coinciding with the axis of the tube. The current varies as $\mathrm{I}=\mathrm{I}_{0} \mathrm{cos}$ (300t) where $I_{0}$ is constant. If the magnetic moment of the loop is , then ‘N’ is
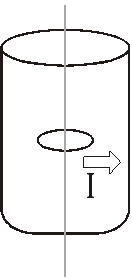[JEE 2011]
[JEE 2011]
Ans. 6
$\phi=\mathrm{B} \pi \mathrm{r}^{2}=\left(\frac{\mu_{0} I}{L}\right) \pi r^{2}=\mu_{0} I_{0} \frac{\pi r^{2}}{L} \cos 300 t \Rightarrow \varepsilon_{1}=\frac{d \phi}{d t}=\left(\frac{\mu_{0} I_{0} \pi r^{2}}{L}\right) 300 \sin 300 t$
$\mathrm{i}=\frac{\varepsilon}{R}=\left(\mu_{0} I_{0} \sin 300 t\right)\left[\frac{\pi r^{2}(300)}{L R}\right] \Rightarrow M=i \pi r^{2}=\left[\frac{\pi^{2} r^{4}(300)}{L R}\right] \mu_{0} I_{0} \sin 300 t$
Q. A circular wire loop of radius R is placed in the x-y plane centred at the origin O. A square loop of side a (a<
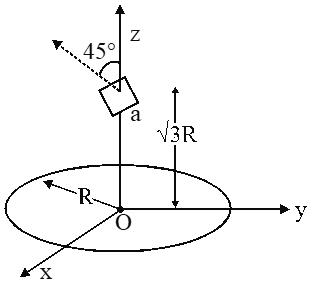[JEE 2012]
[JEE 2012]
Ans. 7
Magnetic field at a distance x along axis of a circular coil is given by $B(x)=\frac{\mu_{0} i R^{2}}{2\left(R^{2}+x^{2}\right)^{3 / 2}}$
$\phi(x)=\left[\frac{\mu_{0} i R^{2}}{2\left(R^{2}+x^{2}\right)^{3 / 2}}\right] N\left(a^{2}\right)\left(\cos 45^{\circ}\right)$
As $\mathrm{P}=\mathrm{Mi} \quad$ So $\mathrm{M}=\frac{\mu_{0} R^{2}(2)}{2\left[R^{2}+(\sqrt{3} R)^{2}\right]^{3 / 2}}\left(\frac{a^{2}}{\sqrt{2}}\right)=\frac{\mu_{0} a^{2}}{2^{7 / 2} R}$ thus $p=7$
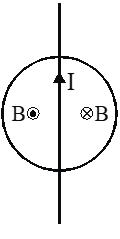
Q. A current carrying infinitely long wire is kept along the diameter of a circular wire loop, without touching it. The correct statement(s) is (are)
(A) The emf induced in the loop is zero if the current is constant.
(B) The emf induced in the loop is infinite if the current is constant.
(C) The emf induced in the loop is zero if the current decreases at a steady rate.
(D) The emf induced in the loop is finite if the current decreases at a steady rate.
[JEE 2012]
Ans. (A,C)
Since flux of wire on the loop is zero therefore emf will not be induced.
Q. The change in the magnetic dipole moment associated with the orbit, at the end of the time interval of the magnetic field change is
$(\mathrm{A})-\gamma \mathrm{B} \mathrm{Q} \mathrm{R}^{2}$
$(\mathrm{B})-\gamma \frac{\mathrm{BQR}^{2}}{2}$
(C) $\gamma \frac{\mathrm{BQR}^{2}}{2}$
(D) $\gamma \mathrm{BQR}^{2}$
[JEE Advance-2013]
Ans. (B)
induce electric field $=\frac{\mathrm{R}}{2} \frac{\mathrm{d} \mathrm{B}}{\mathrm{dt}}=\frac{\mathrm{BR}}{2}$
torque on charge $=\frac{\mathrm{QBR}^{2}}{2}(-\hat{\mathrm{k}})$
by $\vec{\tau}=\frac{\mathrm{d} \overrightarrow{\mathrm{L}}}{\mathrm{dt}} \Rightarrow \int \mathrm{d} \overrightarrow{\mathrm{L}}=\int_{0}^{1} \vec{\tau} \mathrm{dt}$
$\Delta \overrightarrow{\mathrm{L}}=\frac{\mathrm{QBR}^{2}}{2}(-\hat{\mathrm{k}})$
Change in magnetic dipole moment $=\gamma \Delta \overrightarrow{\mathrm{L}}$
$=\frac{\gamma \mathrm{QBR}^{2}}{2}(-\hat{\mathrm{k}})$
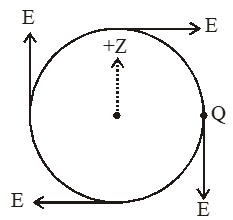
Q. The magnitude of the induced electric field in the orbit at any instant of time during the time interval of the magnetic field change is
(A) $\frac{\mathrm{BR}}{4}$
(B) $\frac{\mathrm{BR}}{2}$
(C) BR
(D) 2BR
[JEE Advance-2013]
Ans. (B)
Magnitude of induced electric field $=\frac{\mathrm{R}}{2} \frac{\mathrm{dB}}{\mathrm{dt}}=\frac{\mathrm{BR}}{2}$
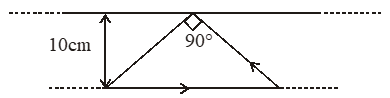
Q. A conducting loop in the shape of right angled isosceles triangle of height 10 cm is kept such that the $90^{\circ}$ vertex is very close to an infinitely long conducting wire (see the figure). The wire is electrically insulated from the loop. The hypotenuse of the triangle is parallel to the wire. The current in the triangular loop is in counterclockwise direction and increased at constant rate of 10 $\mathrm{A} \mathrm{s}^{-1}$. Which of the following statement(s) is(are) true?
(A) The induced current in the wire is in opposite direction to the current along the hypotenuse.
(B) There is a repulsive force between the wire and the loop
(C) If the loop is rotated at a constant angular speed about the wire, an additional emf of $\left(\frac{\mu_{0}}{\pi}\right)$ volt is induced in the wire
(D) The magnitude of induced emf in the wire is $\left(\frac{\mu_{0}}{\pi}\right)$ volt.
[JEE Advance-2013]
[JEE Advance-2013]
Ans. (B,D)
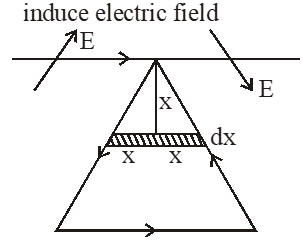by direction of induced electric field, current in wire is in same direction of current along the hypotenuse.
Flux through triangle if wire have current $i=\int_{0}^{0.1}\left(\frac{\mu_{0} i}{2 \pi \mathrm{x}}\right)(2 \mathrm{xd} \mathrm{x})=\frac{\mu_{0} \mathrm{i}}{10 \pi}$
$\Rightarrow$ Mutual inductance $=\frac{\mu_{0}}{10 \pi}$
Induced emf in wire $=\frac{\mu_{0}}{10 \pi} \frac{\mathrm{d} \mathrm{i}}{\mathrm{dt}}=\frac{\mu_{0}}{10 \pi} \times 10=\frac{\mu_{0}}{\pi}$
by direction of induced electric field, current in wire is in same direction of current along the hypotenuse.
Flux through triangle if wire have current $i=\int_{0}^{0.1}\left(\frac{\mu_{0} i}{2 \pi \mathrm{x}}\right)(2 \mathrm{xd} \mathrm{x})=\frac{\mu_{0} \mathrm{i}}{10 \pi}$
$\Rightarrow$ Mutual inductance $=\frac{\mu_{0}}{10 \pi}$
Induced emf in wire $=\frac{\mu_{0}}{10 \pi} \frac{\mathrm{d} \mathrm{i}}{\mathrm{dt}}=\frac{\mu_{0}}{10 \pi} \times 10=\frac{\mu_{0}}{\pi}$
Q. Two inductors $\mathrm{L}_{1}$ (inductance 1 mH, internal resistance 3 $\Omega$) and L2 (inductance 2mH, internal resistance 4$\Omega$), and a resistor R (resistance 12 $\Omega$) are all connected in parallel across a 5V battery. The circuit is switched on at time t = 0. The ratio of the maximum to the minimum current $\left(I_{\max } / I_{\min }\right.$) drawn from the battery is ?
[JEE Advance-2016]
Ans. 8
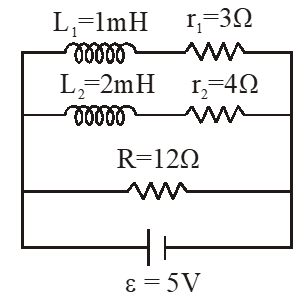$\left.\mathrm{I}_{\max }=\frac{\varepsilon}{\mathrm{R}}=\frac{5}{12} \mathrm{A} \text { (Initially at } \mathrm{t}=0\right)$
$\mathrm{I}_{\min }=\frac{\varepsilon}{\mathrm{R}_{\mathrm{eq}}}=\varepsilon\left(\frac{1}{\mathrm{r}_{1}}+\frac{1}{\mathrm{r}_{2}}+\frac{1}{\mathrm{R}}\right) \quad$ (finally in steady state)
$=5\left(\frac{1}{3}+\frac{1}{4}+\frac{1}{12}\right)$
$=\frac{10}{3} \mathrm{A}$
$\frac{\mathrm{I}_{\max }}{\mathrm{I}_{\min }}=8$
$\left.\mathrm{I}_{\max }=\frac{\varepsilon}{\mathrm{R}}=\frac{5}{12} \mathrm{A} \text { (Initially at } \mathrm{t}=0\right)$
$\mathrm{I}_{\min }=\frac{\varepsilon}{\mathrm{R}_{\mathrm{eq}}}=\varepsilon\left(\frac{1}{\mathrm{r}_{1}}+\frac{1}{\mathrm{r}_{2}}+\frac{1}{\mathrm{R}}\right) \quad$ (finally in steady state)
$=5\left(\frac{1}{3}+\frac{1}{4}+\frac{1}{12}\right)$
$=\frac{10}{3} \mathrm{A}$
$\frac{\mathrm{I}_{\max }}{\mathrm{I}_{\min }}=8$
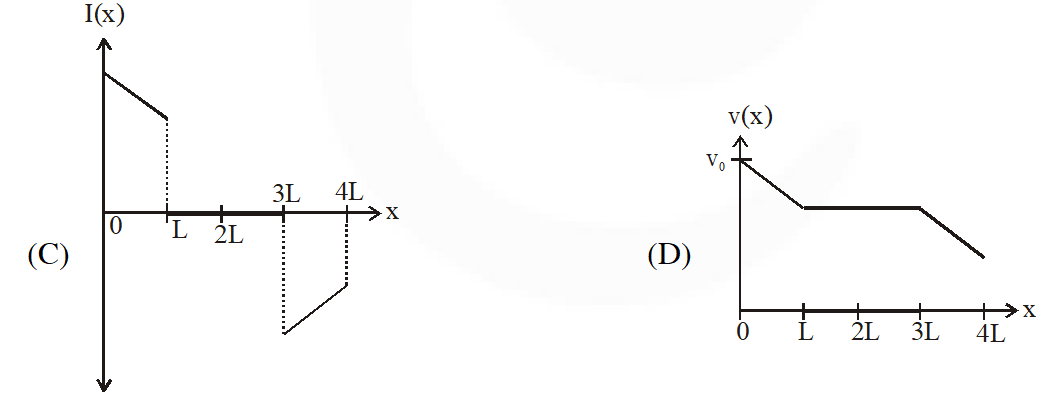
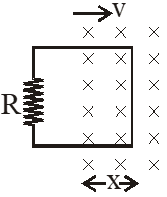
Q. A rigid wire loop of square shape having side of length L and resistance R is moving along the x-axis with a constant velocity $\mathrm{v}_{0}$ in the plane of the paper. At t = 0, the right edge of the loop enters a region of length 3L where there is a uniform magnetic field $B_{0}$ into the plane of the paper, as shown in the figure. For sufficiently large $\mathrm{V}_{\mathrm{o}}$, the loop eventually crosses the region. Let x be the location of the right edge of the loop. Let v(x), I(x) and F(x) represent the velocity of the loop, current in the loop, and force on the loop, respectively, as a function of x. Counter-clockwise current is taken as positive. Which of the following schematic plot(s) is(are) correct ? (Ignore gravity)
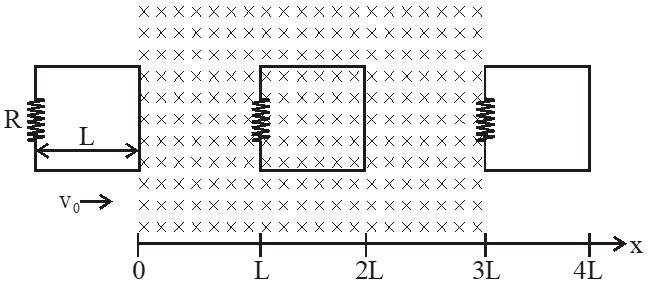
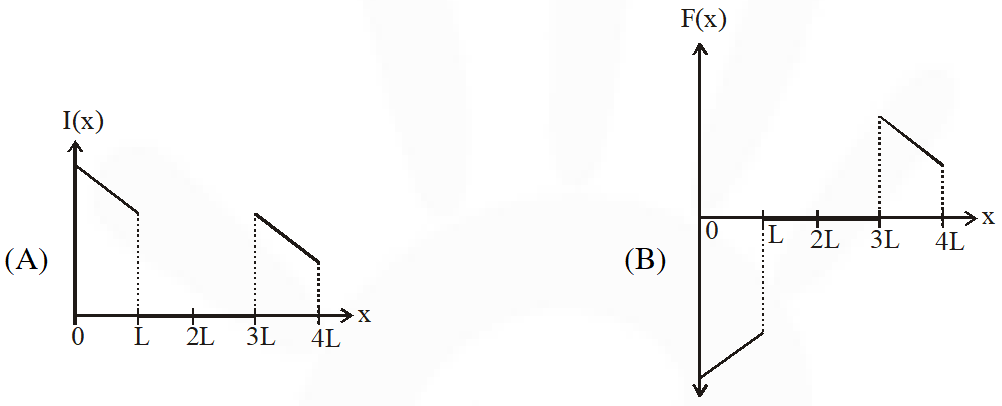
[JEE Advance-2016]
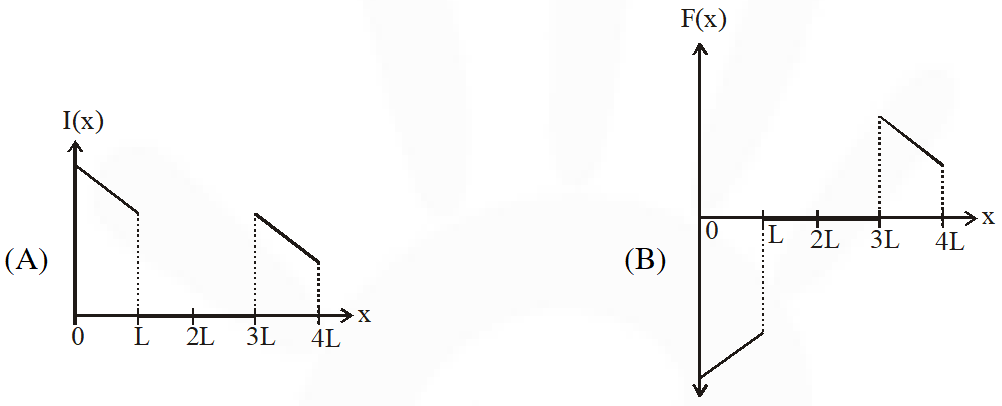
[JEE Advance-2016]
Ans. (C,D)
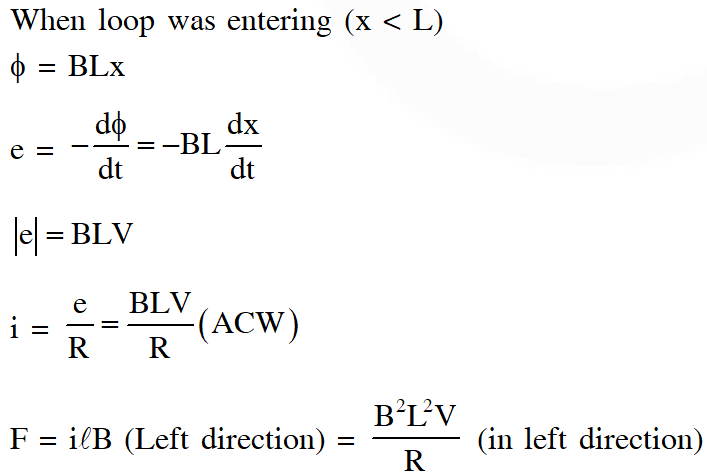
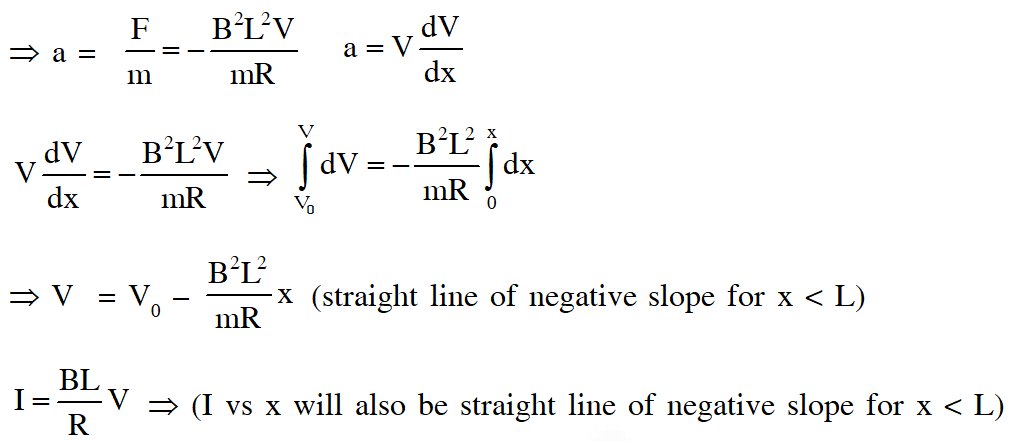
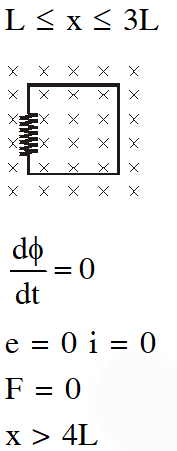
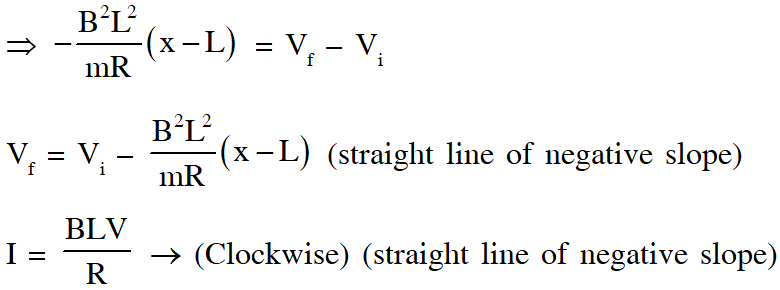
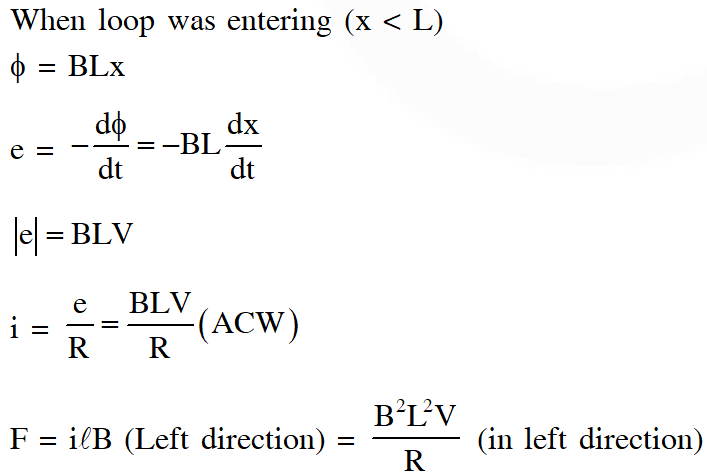
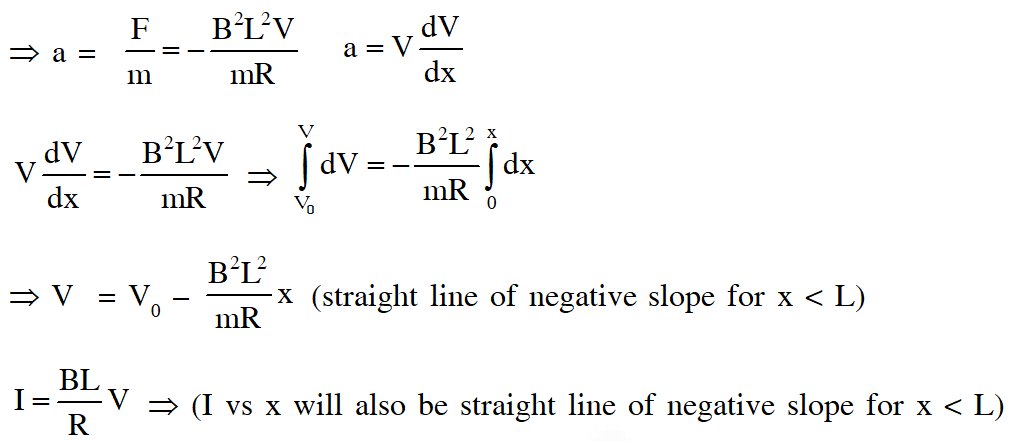
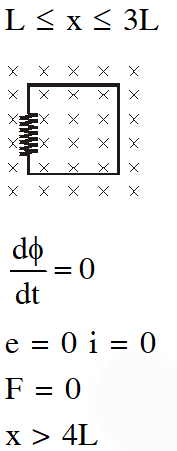
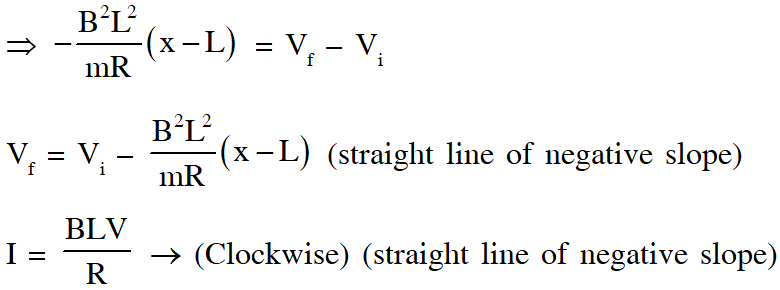
Q. A circular insulated copper wire loop is twisted to form two loops of area A and 2A as shown in the figure. At the point of crossing the wires remain electrically insulated from each other. The entire loop lies in the plane (of the paper). A uniform magnetic field points into the plane of the paper. At t = 0, the loop starts rotating about the common diameter as axis with a constant angular velocity in the magnetic field. Which of the following options is/are correct?
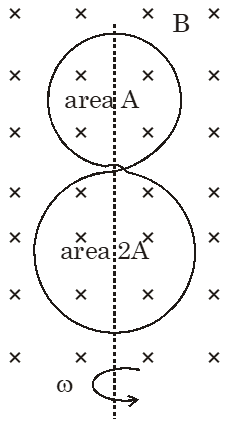(A) The rate of change of the flux is maximum when the plane of the loops is perpendicular to plane of the paper
(B) The net emf induced due to both the loops is proportional to $\cos \omega t$
(C) The emf induced in the loop is proportional to the sum of the areas of the two loops
(D) The amplitude of the maximum net emf induced due to both the loops is equal to the
amplitude of maximum emf induced in the smaller loop alone
[JEE Advance-2017]
(A) The rate of change of the flux is maximum when the plane of the loops is perpendicular to plane of the paper
(B) The net emf induced due to both the loops is proportional to $\cos \omega t$
(C) The emf induced in the loop is proportional to the sum of the areas of the two loops
(D) The amplitude of the maximum net emf induced due to both the loops is equal to the
amplitude of maximum emf induced in the smaller loop alone
[JEE Advance-2017]
Ans. (A,D)
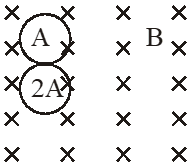
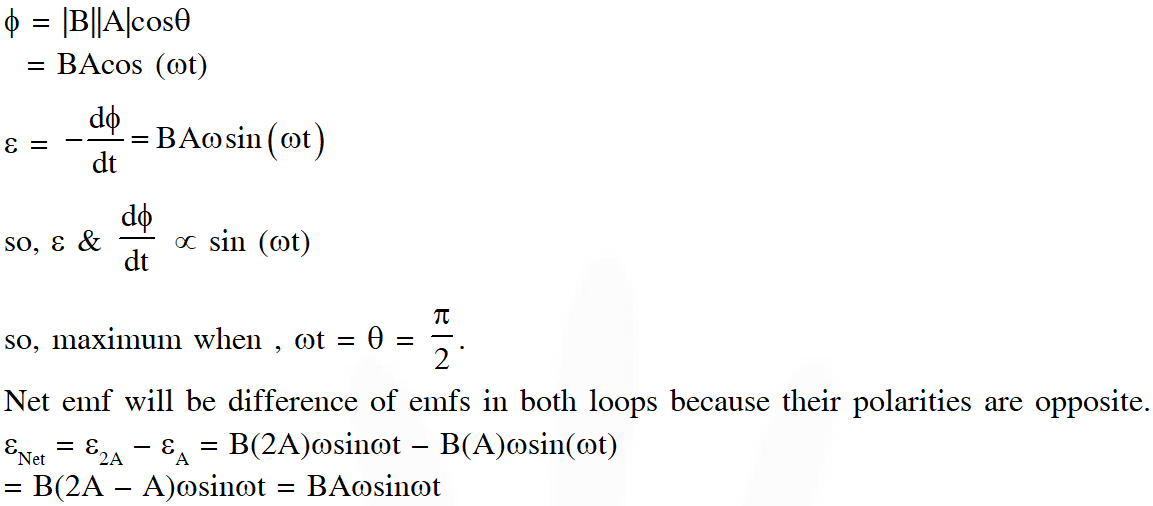
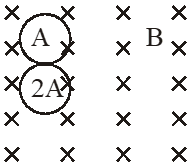
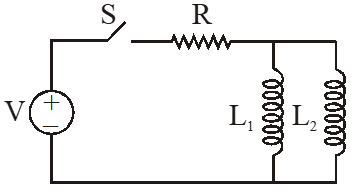
Q. A source of constant voltage V is connected to a resistance R and two ideal inductors $\mathrm{L}_{1}$ and $\mathrm{L}_{2}$ through a switch S as shown. There is no mutual inductance between the two inductors. The switch S is initially open. At t = 0, the switch is closed and current begins to flow. Which of the following options is/are correct?
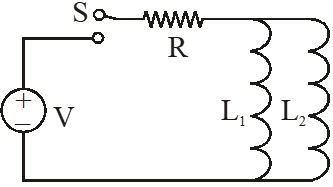(A) The ratio of the currents through $\mathrm{L}_{1}$ and $\mathrm{L}_{2}$ is fixed at all times $(\mathrm{t}>0)$
(B) After a long time, the current through $L_{1}$ will be $\frac{V}{R} \frac{L_{2}}{L_{1}+L_{2}}$
(C) After a long time, the current through $\mathrm{L}_{2}$ will be $\frac{\mathrm{V}}{\mathrm{R}} \frac{\mathrm{L}_{1}}{\mathrm{L}_{1}+\mathrm{L}_{2}}$
(D) At $\mathrm{t}=0,$ the current through the resistance $\mathrm{R}$ is $\frac{\mathrm{V}}{\mathrm{R}}$
[JEE Advance-2017]
(A) The ratio of the currents through $\mathrm{L}_{1}$ and $\mathrm{L}_{2}$ is fixed at all times $(\mathrm{t}>0)$
(B) After a long time, the current through $L_{1}$ will be $\frac{V}{R} \frac{L_{2}}{L_{1}+L_{2}}$
(C) After a long time, the current through $\mathrm{L}_{2}$ will be $\frac{\mathrm{V}}{\mathrm{R}} \frac{\mathrm{L}_{1}}{\mathrm{L}_{1}+\mathrm{L}_{2}}$
(D) At $\mathrm{t}=0,$ the current through the resistance $\mathrm{R}$ is $\frac{\mathrm{V}}{\mathrm{R}}$
[JEE Advance-2017]
Ans. (A,B,C)
Since inductors are connected in parallel
$\mathrm{V}_{\mathrm{L}_{1}}=\mathrm{V}_{\mathrm{L}_{2}}$
$\mathrm{L}_{1} \frac{\mathrm{dI}_{1}}{\mathrm{dt}}=\mathrm{L}_{2} \frac{\mathrm{d} \mathrm{I}_{2}}{\mathrm{dt}}$
$\mathrm{L}_{1} \mathrm{I}_{1}=\mathrm{L}_{2} \mathrm{I}_{2}$
$\frac{\mathrm{I}_{1}}{\mathrm{I}_{2}}=\frac{\mathrm{L}_{2}}{\mathrm{L}_{1}}$
Current through resistor at any time t is given by
$\left.\mathrm{I}=\mathrm{V} / \mathrm{R}_{(1-\mathrm{e}}^{-\frac{\mathrm{RT}}{\mathrm{L}}}\right)$ where $\mathrm{L}=\frac{\mathrm{L}_{1} \mathrm{L}_{2}}{\mathrm{L}_{1}+\mathrm{L}_{2}}$
After long time I $=\frac{\mathrm{V}}{\mathrm{R}}$
$\mathrm{I}_{1}+\mathrm{I}_{2}=\mathrm{I} \quad \ldots(\mathrm{i})$
$\mathrm{L}_{1} \mathrm{I}_{1}=\mathrm{L}_{2} \mathrm{I}_{2} \quad \ldots$ (ii)
From (i) & (ii) we get
$\mathrm{I}_{1}=\frac{\mathrm{V}}{\mathrm{R}} \frac{\mathrm{L}_{2}}{\mathrm{L}_{1}+\mathrm{L}_{2}}, \quad \mathrm{I}_{2}=\frac{\mathrm{V}}{\mathrm{R}} \frac{\mathrm{L}_{1}}{\mathrm{L}_{1}+\mathrm{L}_{2}}$
(D) value of current is zero at t = 0
value of current is $\mathrm{V} / \mathrm{R}$ at $\mathrm{t}=\infty$
Hence option (D) is incorrect.
Since inductors are connected in parallel
$\mathrm{V}_{\mathrm{L}_{1}}=\mathrm{V}_{\mathrm{L}_{2}}$
$\mathrm{L}_{1} \frac{\mathrm{dI}_{1}}{\mathrm{dt}}=\mathrm{L}_{2} \frac{\mathrm{d} \mathrm{I}_{2}}{\mathrm{dt}}$
$\mathrm{L}_{1} \mathrm{I}_{1}=\mathrm{L}_{2} \mathrm{I}_{2}$
$\frac{\mathrm{I}_{1}}{\mathrm{I}_{2}}=\frac{\mathrm{L}_{2}}{\mathrm{L}_{1}}$
Current through resistor at any time t is given by
$\left.\mathrm{I}=\mathrm{V} / \mathrm{R}_{(1-\mathrm{e}}^{-\frac{\mathrm{RT}}{\mathrm{L}}}\right)$ where $\mathrm{L}=\frac{\mathrm{L}_{1} \mathrm{L}_{2}}{\mathrm{L}_{1}+\mathrm{L}_{2}}$
After long time I $=\frac{\mathrm{V}}{\mathrm{R}}$
$\mathrm{I}_{1}+\mathrm{I}_{2}=\mathrm{I} \quad \ldots(\mathrm{i})$
$\mathrm{L}_{1} \mathrm{I}_{1}=\mathrm{L}_{2} \mathrm{I}_{2} \quad \ldots$ (ii)
From (i) & (ii) we get
$\mathrm{I}_{1}=\frac{\mathrm{V}}{\mathrm{R}} \frac{\mathrm{L}_{2}}{\mathrm{L}_{1}+\mathrm{L}_{2}}, \quad \mathrm{I}_{2}=\frac{\mathrm{V}}{\mathrm{R}} \frac{\mathrm{L}_{1}}{\mathrm{L}_{1}+\mathrm{L}_{2}}$
(D) value of current is zero at t = 0
value of current is $\mathrm{V} / \mathrm{R}$ at $\mathrm{t}=\infty$
Hence option (D) is incorrect.
Q. In the figure below, the switches $\mathrm{S}_{1}$ and $\mathrm{S}_{2}$ are closed simultaneously at t = 0 and a current starts to flow in the circuit. Both the batteries have the same magnitude of the electromotive force (emf) and the polarities are as indicated in the figure. Ignore mutual inductance between the inductors. The current I in the middle wire reaches its maximum magnitude $\mathrm{I}_{\mathrm{max}}$ at time $t=\tau$. Which of the following statement(s) is (are) true?
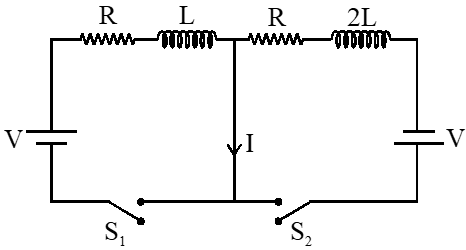(A) $\mathrm{I}_{\max }=\frac{\mathrm{V}}{2 \mathrm{R}}$
(B) $\mathrm{I}_{\max }=\frac{\mathrm{V}}{4 \mathrm{R}}$
(C) $\tau=\frac{\mathrm{L}}{\mathrm{R}} \ell \mathrm{n} 2$
(D) $\tau=\frac{2 \mathrm{L}}{\mathrm{R}} \ell \mathrm{n} 2$
[JEE Advance-2017]
(A) $\mathrm{I}_{\max }=\frac{\mathrm{V}}{2 \mathrm{R}}$
(B) $\mathrm{I}_{\max }=\frac{\mathrm{V}}{4 \mathrm{R}}$
(C) $\tau=\frac{\mathrm{L}}{\mathrm{R}} \ell \mathrm{n} 2$
(D) $\tau=\frac{2 \mathrm{L}}{\mathrm{R}} \ell \mathrm{n} 2$
[JEE Advance-2017]
Ans. (B,D)
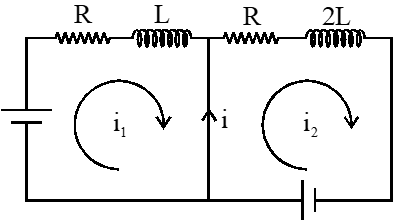$\mathrm{i}_{\max }=\left(\mathrm{i}_{2}-\mathrm{i}_{1}\right)_{\max }$
$\Delta \mathrm{i}=\left(\mathrm{i}_{2}-\mathrm{i}_{1}\right)=\frac{\mathrm{V}}{\mathrm{R}}\left[1-\mathrm{e}^{-\left(\frac{\mathrm{R}}{2 \mathrm{L}}\right) \mathrm{t}}\right]-\frac{\mathrm{V}}{\mathrm{R}}\left[1-\mathrm{e}^{\left(-\frac{\mathrm{R}}{\mathrm{L}}\right) \mathrm{t}}\right]$
$\frac{V}{R}\left[e^{-\left(\frac{R}{L}\right) t}-e^{-\left(\frac{R}{2 L}\right) t}\right]$
For $(\Delta \mathrm{i})_{\max } \frac{\mathrm{d}(\Delta \mathrm{i})}{\mathrm{dt}}=0$
$\frac{\mathrm{V}}{\mathrm{R}}\left[-\frac{\mathrm{R}}{\mathrm{L}} \mathrm{e}^{-\left(\frac{\mathrm{R}}{\mathrm{L}}\right) \mathrm{t}}-\left(-\frac{\mathrm{R}}{2 \mathrm{L}}\right) \mathrm{e}^{-\left(\frac{\mathrm{R}}{2 \mathrm{L}}\right) \mathrm{t}}\right]=0$
$\mathrm{e}^{-\left(\frac{\mathrm{R}}{\mathrm{L}}\right) \mathrm{t}}=\frac{1}{2} \mathrm{e}^{-\left(\frac{\mathrm{R}}{2 \mathrm{L}}\right) \mathrm{t}}$
$\mathrm{e}^{-\left(\frac{\mathrm{R}}{2 \mathrm{L}}\right) \mathrm{t}}=\frac{1}{2}$
$\left(\frac{\mathrm{R}}{2 \mathrm{L}}\right) \mathrm{t}=\ell \mathrm{n} 2$
$\mathrm{t}=\frac{2 \mathrm{L}}{\mathrm{R}} \ell \mathrm{n} 2 \rightarrow$ time when $\mathrm{i}$ is maximum.
$\dot{\mathbf{i}}_{\max }=\frac{V}{R}\left[e^{-\frac{R}{L}\left(\frac{2 L}{R} \ell_{n} 2\right)}-e^{-\left(\frac{R}{2 L}\right)\left(\frac{2 L}{R} \ln 2\right)}\right]$
$\left|\mathrm{i}_{\max }\right|=\frac{\mathrm{V}}{\mathrm{R}}\left|\left[\frac{1}{4}-\frac{1}{2}\right]\right|=\frac{1}{4} \frac{\mathrm{V}}{\mathrm{R}}$
$\mathrm{I}_{1}=\frac{\mathrm{V}}{\mathrm{R}} \frac{\mathrm{L}_{2}}{\mathrm{L}_{1}+\mathrm{L}_{2}}, \quad \mathrm{I}_{2}=\frac{\mathrm{V}}{\mathrm{R}} \frac{\mathrm{L}_{1}}{\mathrm{L}_{1}+\mathrm{L}_{2}}$
(D) value of current is zero at t = 0
value of current is $\mathrm{V} / \mathrm{R}$ at $\mathrm{t}=\infty$
Hence option (D) is incorrect.
$\mathrm{i}_{\max }=\left(\mathrm{i}_{2}-\mathrm{i}_{1}\right)_{\max }$
$\Delta \mathrm{i}=\left(\mathrm{i}_{2}-\mathrm{i}_{1}\right)=\frac{\mathrm{V}}{\mathrm{R}}\left[1-\mathrm{e}^{-\left(\frac{\mathrm{R}}{2 \mathrm{L}}\right) \mathrm{t}}\right]-\frac{\mathrm{V}}{\mathrm{R}}\left[1-\mathrm{e}^{\left(-\frac{\mathrm{R}}{\mathrm{L}}\right) \mathrm{t}}\right]$
$\frac{V}{R}\left[e^{-\left(\frac{R}{L}\right) t}-e^{-\left(\frac{R}{2 L}\right) t}\right]$
For $(\Delta \mathrm{i})_{\max } \frac{\mathrm{d}(\Delta \mathrm{i})}{\mathrm{dt}}=0$
$\frac{\mathrm{V}}{\mathrm{R}}\left[-\frac{\mathrm{R}}{\mathrm{L}} \mathrm{e}^{-\left(\frac{\mathrm{R}}{\mathrm{L}}\right) \mathrm{t}}-\left(-\frac{\mathrm{R}}{2 \mathrm{L}}\right) \mathrm{e}^{-\left(\frac{\mathrm{R}}{2 \mathrm{L}}\right) \mathrm{t}}\right]=0$
$\mathrm{e}^{-\left(\frac{\mathrm{R}}{\mathrm{L}}\right) \mathrm{t}}=\frac{1}{2} \mathrm{e}^{-\left(\frac{\mathrm{R}}{2 \mathrm{L}}\right) \mathrm{t}}$
$\mathrm{e}^{-\left(\frac{\mathrm{R}}{2 \mathrm{L}}\right) \mathrm{t}}=\frac{1}{2}$
$\left(\frac{\mathrm{R}}{2 \mathrm{L}}\right) \mathrm{t}=\ell \mathrm{n} 2$
$\mathrm{t}=\frac{2 \mathrm{L}}{\mathrm{R}} \ell \mathrm{n} 2 \rightarrow$ time when $\mathrm{i}$ is maximum.
$\dot{\mathbf{i}}_{\max }=\frac{V}{R}\left[e^{-\frac{R}{L}\left(\frac{2 L}{R} \ell_{n} 2\right)}-e^{-\left(\frac{R}{2 L}\right)\left(\frac{2 L}{R} \ln 2\right)}\right]$
$\left|\mathrm{i}_{\max }\right|=\frac{\mathrm{V}}{\mathrm{R}}\left|\left[\frac{1}{4}-\frac{1}{2}\right]\right|=\frac{1}{4} \frac{\mathrm{V}}{\mathrm{R}}$
$\mathrm{I}_{1}=\frac{\mathrm{V}}{\mathrm{R}} \frac{\mathrm{L}_{2}}{\mathrm{L}_{1}+\mathrm{L}_{2}}, \quad \mathrm{I}_{2}=\frac{\mathrm{V}}{\mathrm{R}} \frac{\mathrm{L}_{1}}{\mathrm{L}_{1}+\mathrm{L}_{2}}$
(D) value of current is zero at t = 0
value of current is $\mathrm{V} / \mathrm{R}$ at $\mathrm{t}=\infty$
Hence option (D) is incorrect.