JEE Main Previous Year Question of Math with Solutions are available at eSaral. Practicing JEE Main Previous Year Papers Questions of mathematics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
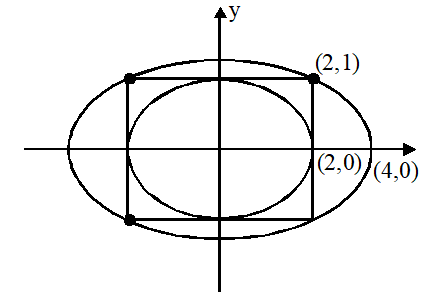
Q. The ellipse $x^{2}+4 y^{2}=4$ is inscribed in a rectangle aligned with the coordinate axes, which in turn is inscribed in another ellipse that passes through the point (4, 0). Then the equation of the ellipse is :-
(1) $4 x^{2}+48 y^{2}=48$
(2) $4 x^{2}+64 y^{2}=48$
(3) $x^{2}+16 y^{2}=16$
(4) $x^{2}+12 y^{2}=16$
[AIEEE-2009]
Ans. (4)
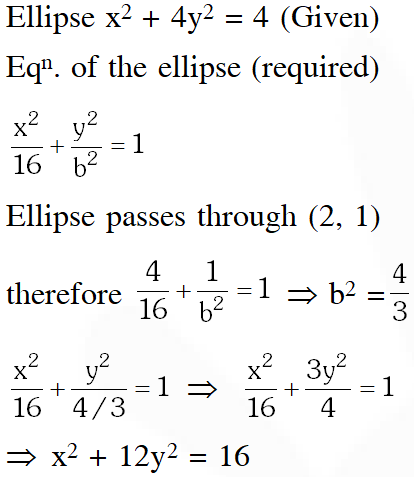
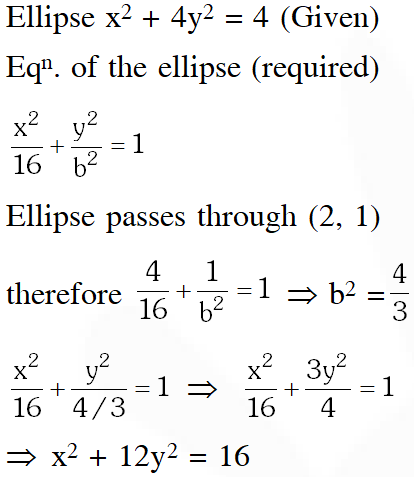
Q. Equation of the ellipse whose axes are the axes of coordinates and which passes through the point (–3, 1) and has eccentricity $\sqrt{2 / 5}$ is :-
(1) $3 x^{2}+5 y^{2}-15=0$
(2) $5 x^{2}+3 y^{2}-32=0$
(3) $3 x^{2}+5 y^{2}-32=0$
(4) $5 x^{2}+3 y^{2}-48=0$
[AIEEE-2011]
Ans. (3)
$\frac{\mathrm{x}^{2}}{\mathrm{a}^{2}}+\frac{\mathrm{y}^{2}}{\mathrm{b}^{2}}=1 \mathrm{e}=\sqrt{\frac{2}{5}}$
It passes through $(-3,1)$ so $\frac{9}{a^{2}}+\frac{1}{b^{2}}=1$ .....(1)
also $1-\frac{b^{2}}{a^{2}}=e^{2} \Rightarrow 1-\frac{b^{2}}{a^{2}}=\frac{2}{5}$
$\frac{b^{2}}{a^{2}}=\frac{3}{5}$ .....(2)
solve $(1) \&(2) \mathrm{a}^{2}=\frac{32}{3}, \mathrm{b}^{2}=\frac{32}{5} 0$
Q. An ellipse is drawn by taking a diameter of the circle $(x-1)^{2}+y^{2}=1$ as its semi-minor axis and a diameter of the circle $x^{2}+(y-2)^{2}=4$ as its semi-major axis. If the centre of
the ellipse is at the origin and its axes are the coordinate axes, then the equation of the
ellipse is :
(1) $x^{2}+4 y^{2}=16$
(2) $4 x^{2}+y^{2}=4$
(3) $x^{2}+4 y^{2}=8$
(4) $4 x^{2}+y^{2}=8$
[AIEEE-2012]
Ans. (1)
Let the equation of ellipse be
$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$
from the given conditions
$\mathrm{a}=4$ and $\mathrm{b}=2$
$\therefore \mathrm{Eq}$ of ellipse is $\frac{\mathrm{x}^{2}}{16}+\frac{\mathrm{y}^{2}}{4}=1$
or $\mathrm{x}^{2}+4 \mathrm{y}^{2}=16$
Q. Statement-1: An equation of a common tangent to the parabola $\mathrm{y}^{2}=16 \sqrt{3} \mathrm{x}$ and the
ellipse $2 \mathrm{x}^{2}+\mathrm{y}^{2}=4$ is $\mathrm{y}=2 \mathrm{x}+2 \sqrt{3}$
Statement-2: If the line $y=m x+\frac{4 \sqrt{3}}{m},(m \neq 0)$ is a common tangent to the parabola $y^{2}=$ $$
16 \sqrt{3} x \text { and the ellipse } 2 x^{2}+y^{2}=4, \text { then } m \text { satisfies } m^{4}+2 m^{2}=24$$
(1) Statement–1 is true, Statement–2 is false.
(2) Statement–1 is false, Statement–2 is true.
(3) Statement–1 is true, Statement–2 is true ; Statement–2 is a correct explanation for Statement–1.
(4) Statement–1 is true, Statement–2 is true ; Statement–2 is not a correct explanation for Statement– 1.
[AIEEE-2012]
Ans. (3)
Let equation of any tangent to $\mathrm{y}^{2}=16 \sqrt{3} \mathrm{x}$
be $\mathrm{y}=\mathrm{mx}+\frac{4 \sqrt{3}}{\mathrm{m}}$
and equation of any tangent to $2 \mathrm{x}^{2}+\mathrm{y}^{2}=4$
be $\mathrm{y}=\mathrm{mx}+\sqrt{2 \mathrm{m}^{2}+4} \ldots \ldots$ (ii)
but $(\mathrm{i})$ and (ii) are same lines
$\therefore \frac{4 \sqrt{3}}{\mathrm{m}}=\sqrt{2 \mathrm{m}^{2}+4}$
$\Rightarrow \mathrm{m}^{4}+2 \mathrm{m}^{2}-24=0$
$\Rightarrow \mathrm{m}^{2}=-6,4$
$\therefore \mathrm{m}=\pm 2$
Q. The equation of the circle passing through the foci of the ellipse $\frac{x^{2}}{16}+\frac{y^{2}}{9}=1$ and having centre at $(0,3)$ is :
(1) $x^{2}+y^{2}-6 y-7=0$
(2) $x^{2}+y^{2}-6 y+7=0$
(3) $x^{2}+y^{2}-6 y-5=0$
(4) $x^{2}+y^{2}-6 y+5=0$
[JEE (Main)-2013]
Ans. (1)
$\frac{x^{2}}{16}+\frac{y^{2}}{9}=1$
$e=\sqrt{1-\frac{b^{2}}{a^{2}}}=\frac{\sqrt{7}}{4}$
foci $(\pm a e, 0) \equiv(\pm \sqrt{7}, 0)$
centre of circle is $(0,3)$
$\mathrm{x}^{2}+\mathrm{y}^{2}-6 \mathrm{y}+\mathrm{c}=0$
passes through $(\sqrt{7}, 0)$
$7+0-0+\mathrm{c}=0$
$\mathrm{c}=-7$
So $\mathrm{x}^{2}+\mathrm{y}^{2}-6 \mathrm{y}-7=0$
Q. If a and $c$ are positive real number and the ellipse $\frac{x^{2}}{4 c^{2}}+\frac{y^{2}}{c^{2}}=1$ has four distinct points in common with the circle $x^{2}+y^{2}=9 a^{2},$ then
(1) $6 \mathrm{ac}+9 \mathrm{a}^{2}-2 \mathrm{c}^{2}>0$
(2) $6 a c+9 a^{2}-2 c^{2}<0$
(3) $9 \mathrm{ac}-9 \mathrm{a}^{2}-2 \mathrm{c}^{2}<0$
(4) $9 \mathrm{ac}-9 \mathrm{a}^{2}-2 \mathrm{c}^{2}>0$
[JEE-Main (On line)-2013]
Ans. (4)
$\mathrm{c}<3 \mathrm{a}<2 \mathrm{c}$
$3 \mathrm{a}-\mathrm{c}>0$
$2 \mathrm{c}-3 \mathrm{a}>0$
$\because(3 \mathrm{a}-\mathrm{c})(2 \mathrm{c}-3 \mathrm{a})>0$
$9 \mathrm{ac}-9 \mathrm{a}^{2}-2 \mathrm{c}^{2}>0$
Q. Equation of the line passing through the points of intersection of the parabola $x^{2}=8 y$ and the ellipse $\frac{x^{2}}{3}+y^{2}=1$ is : -
(1) y + 3 = 0
(2) 3y + 1 = 0
(3) 3y – 1 = 0
(4) y – 3 = 0
[JEE-Main (On line)-2013]
Ans. (3)
Put $x^{2}=8 y$ in $\frac{x^{2}}{3}+y^{2}=1$
$\quad=(y+3)(3 y-1)=0$
$\mathrm{y}+3=0$
$3 \mathrm{y}-1=0$
Q. Let the equations of two ellipses be $\mathrm{E}_{1}: \frac{\mathrm{x}^{2}}{3}+\frac{\mathrm{y}^{2}}{2}=1$ and $\mathrm{E}_{2}: \frac{\mathrm{x}^{2}}{16}+\frac{\mathrm{y}^{2}}{\mathrm{b}^{2}}=1 .$ If the product of their eccentricities is $\frac{1}{2},$ then the length of the minor axis of ellipse $\mathrm{E}_{2}$ is :-
(1) 9 (2) 8 (3) 2 (4) 4
[JEE-Main (On line)-2013]
Ans. (4)
$\mathrm{e}_{1} \mathrm{e}_{2}=\frac{1}{2}$
$\Rightarrow \quad \sqrt{1-\frac{2}{3}} \sqrt{1-\frac{\mathrm{b}^{2}}{16}}=\frac{1}{2} \quad$ if $16>\mathrm{b}^{2}$
$=\left(16-\mathrm{b}^{2}\right)=12$
$=\mathrm{b}^{2}=4 \quad \Rightarrow \mathrm{b}=2$
length of minor axis = 4
Q. If the curves $\frac{x^{2}}{\alpha}+\frac{y^{2}}{4}=1$ and $y^{3}=16 x$ intersect at right angles, then a value of $\alpha$ is :
(1) $\frac{4}{3}$
(2) $\frac{3}{4}$
(3) $\frac{1}{2}$
(4) 2
[JEE-Main (On line)-2013]
Ans. (1)
$\frac{\mathrm{x}^{2}}{\alpha}+\frac{\mathrm{y}^{2}}{4}=1 \& \mathrm{y}^{3}=16 \mathrm{x}$
d.w.r. to x.
$\frac{2 \mathrm{x}}{\alpha}+\frac{\mathrm{y}}{2} \mathrm{y}^{\prime}=0 \quad \& \quad 3 \mathrm{y}^{2} \mathrm{y}^{\prime}=16$
$\mathrm{y}^{\prime}=-\frac{4 \mathrm{x}}{\alpha \mathrm{y}} \& \mathrm{y}^{\prime}=\frac{16}{3 \mathrm{y}^{2}}$
Both are orthogonal $\Rightarrow-\frac{4 \mathrm{x}}{\alpha \mathrm{y}} \cdot \frac{16}{3 \mathrm{y}^{2}}=-1$
$\alpha=\frac{4}{3} \quad$ as $\left(16 \mathrm{x}=\mathrm{y}^{3}\right)$
Q. A point on the ellipse, $4 \mathrm{x}^{2}+9 \mathrm{y}^{2}=36,$ where the normal is parallel to the line, $4 \mathrm{x}-2 \mathrm{y}-5$ $=0,$ is : $-$
(1) $\left(\frac{8}{5},-\frac{9}{5}\right)$
(2) $\left(-\frac{9}{5}, \frac{8}{5}\right)$
( 3)$\left(\frac{8}{5}, \frac{9}{5}\right)$
( 4)$\left(\frac{9}{5}, \frac{8}{5}\right)$
[JEE-Main (On line)-2013]
Ans. (4)
$\frac{\mathrm{x}^{2}}{9}+\frac{\mathrm{y}^{2}}{4}=1$
Any point $(3 \cos \theta, 2 \mathrm{sin} \theta)$
Slope of normal $=2$
Slope of tangent $=-\frac{1}{2}=-\frac{2 \cos \theta}{3 \sin \theta}$
$\tan \theta=\frac{4}{3}$
$\sin \theta=\frac{4}{5} \quad \cos \theta=\frac{3}{5}$
Point $\left(\frac{9}{5}, \frac{8}{5}\right)$
Q. The locus of the foot of perpendicular drawn from the centre of the ellipse $x^{2}+3 y^{2}=6$ on any tangent to it is :-
(1) $\left(x^{2}-y^{2}\right)^{2}=6 x^{2}+2 y^{2}$
(2) $\left(x^{2}-y^{2}\right)^{2}=6 x^{2}-2 y^{2}$
(3) $\left(x^{2}+y^{2}\right)^{2}=6 x^{2}+2 y^{2}$
(4) $\left(x^{2}+y^{2}\right)^{2}=6 x^{2}-2 y^{2}$
[JEE(Main)-2014]
Ans. (3)
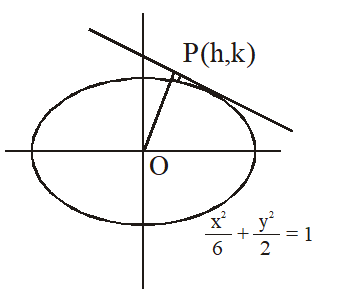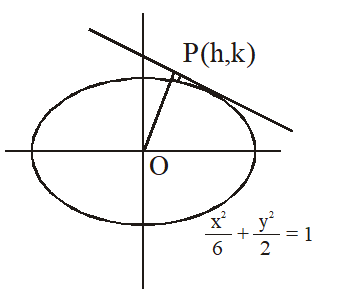Let the foot of perpendicular be (h, k)
then $\mathrm{m}_{\mathrm{op}}=\frac{\mathrm{k}}{\mathrm{h}}$
equation of tangent is $\mathrm{y}=\mathrm{mx} \pm \sqrt{\mathrm{a}^{2} \mathrm{m}^{2}+\mathrm{b}^{2}}$
$\mathrm{y}=\mathrm{mx} \pm \sqrt{6 \mathrm{m}^{2}+2}$
satisfied by $(\mathrm{h}, \mathrm{k})$ and $\mathrm{m}=-\frac{1}{\mathrm{m}_{\mathrm{op}}}=-\frac{\mathrm{h}}{\mathrm{k}}$
$\left(\mathrm{k}+\frac{\mathrm{h}^{2}}{\mathrm{k}}\right)^{2}=\frac{6 \mathrm{h}^{2}}{\mathrm{k}^{2}}+2$
multiply by $\mathrm{k}^{2}$
$\left(\mathrm{k}^{2}+\mathrm{h}^{2}\right)^{2}=6 \mathrm{h}^{2}+2 \mathrm{k}^{2}$
$\Rightarrow\left(\mathrm{x}^{2}+\mathrm{y}^{2}\right)^{2}=6 \mathrm{x}^{2}+2 \mathrm{y}^{2}$
Let the foot of perpendicular be (h, k)
then $\mathrm{m}_{\mathrm{op}}=\frac{\mathrm{k}}{\mathrm{h}}$
equation of tangent is $\mathrm{y}=\mathrm{mx} \pm \sqrt{\mathrm{a}^{2} \mathrm{m}^{2}+\mathrm{b}^{2}}$
$\mathrm{y}=\mathrm{mx} \pm \sqrt{6 \mathrm{m}^{2}+2}$
satisfied by $(\mathrm{h}, \mathrm{k})$ and $\mathrm{m}=-\frac{1}{\mathrm{m}_{\mathrm{op}}}=-\frac{\mathrm{h}}{\mathrm{k}}$
$\left(\mathrm{k}+\frac{\mathrm{h}^{2}}{\mathrm{k}}\right)^{2}=\frac{6 \mathrm{h}^{2}}{\mathrm{k}^{2}}+2$
multiply by $\mathrm{k}^{2}$
$\left(\mathrm{k}^{2}+\mathrm{h}^{2}\right)^{2}=6 \mathrm{h}^{2}+2 \mathrm{k}^{2}$
$\Rightarrow\left(\mathrm{x}^{2}+\mathrm{y}^{2}\right)^{2}=6 \mathrm{x}^{2}+2 \mathrm{y}^{2}$
Q. The area (in sq. units) of the quadrilateral formed by the tangents at the end points of the
latera recta to the ellipse $\frac{x^{2}}{9}+\frac{y^{2}}{5}=1$ is :
(1) $\frac{27}{2}$
(2) 27
(3) $\frac{27}{4}$
(4) 18
[JEE(Main)-2015]
Ans. (2)
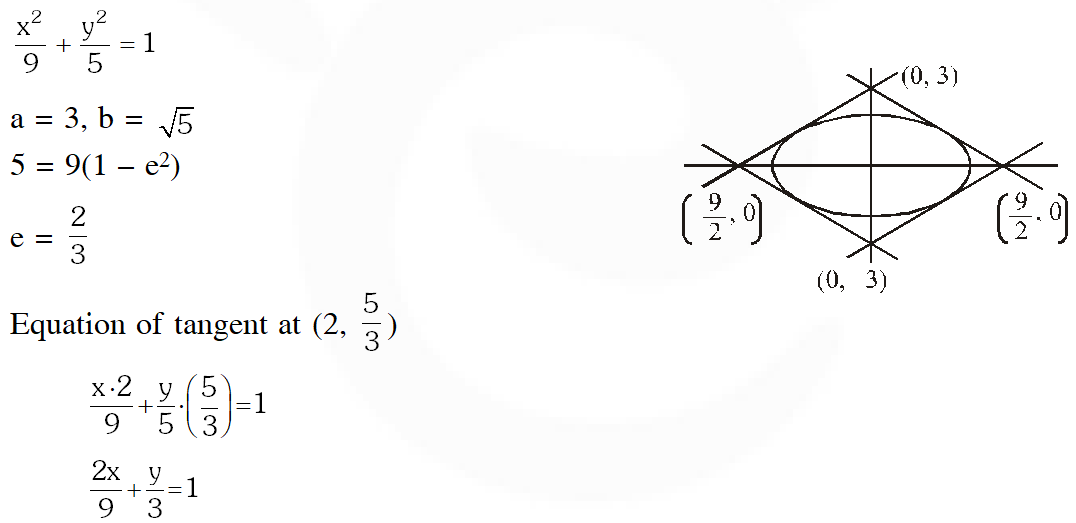
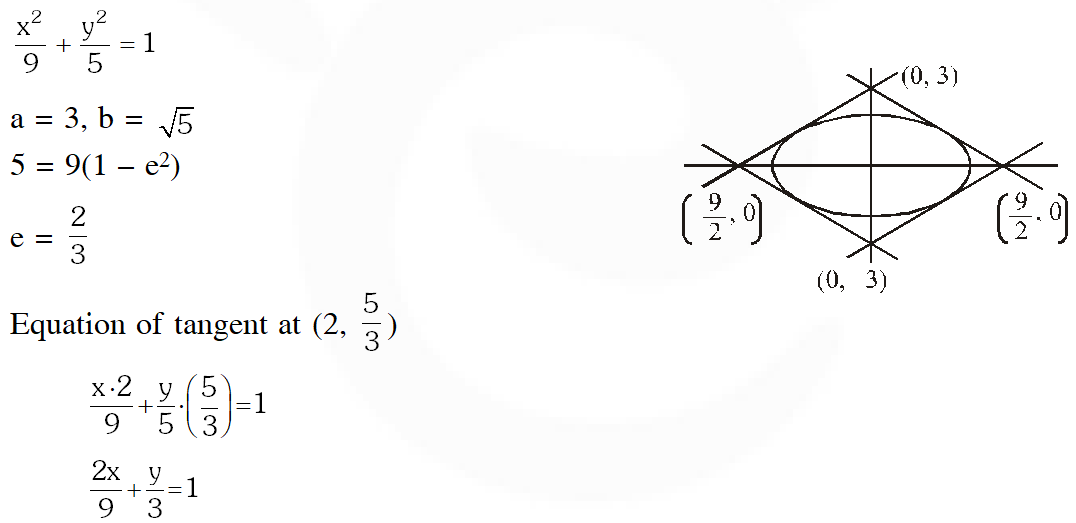
Q. The eccentricity of an ellipse centre is at the origin is $\frac{1}{2} .$ If one of its directices is $\mathrm{x}=-4,$ then the equation of the normal to it at $\left(1, \frac{3}{2}\right)$ is : -
(1) x + 2y = 4
(2) 2y – x = 2
(3) 4x – 2y = 1
(4) 4x + 2y = 7
[JEE(Main)-2017]
Ans. (3)
Eccentricity of ellipse $=\frac{1}{2}$
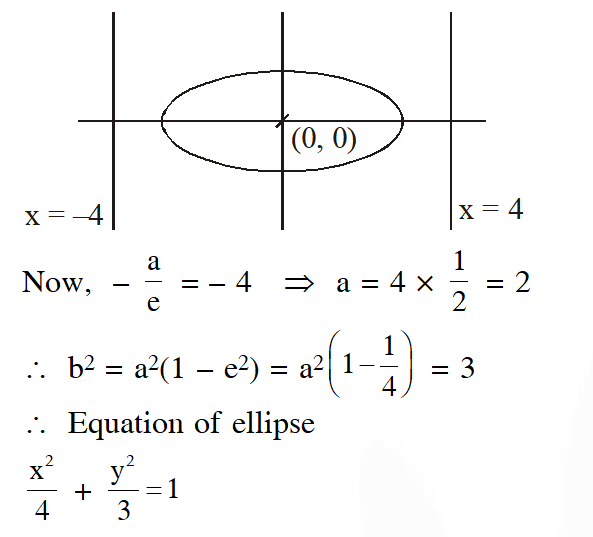
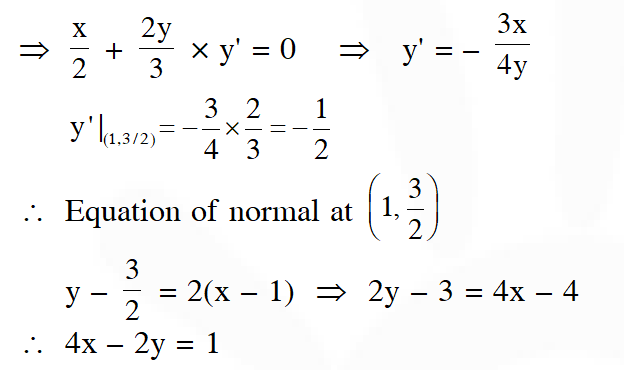
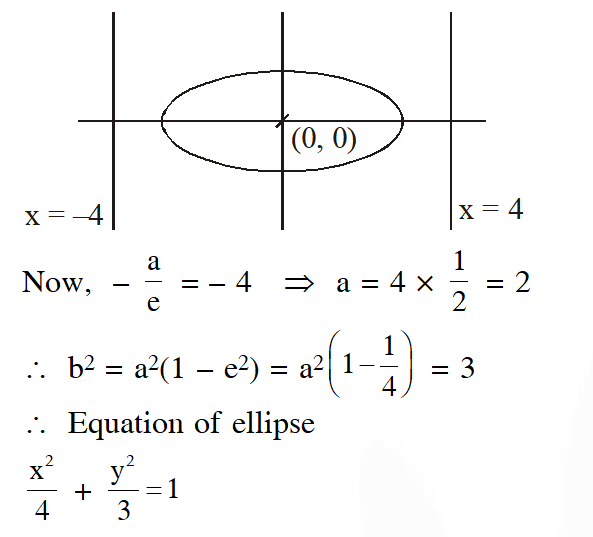
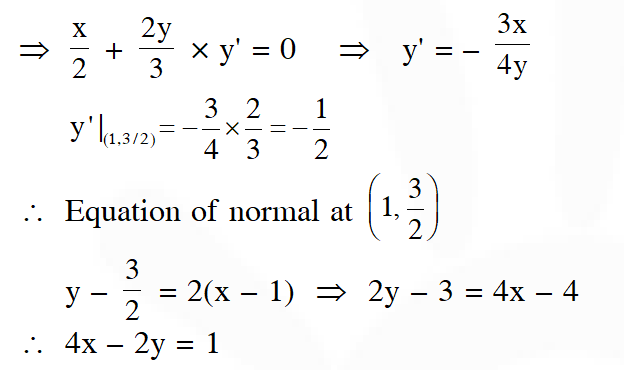
Comments
Suggestion
Aug. 16, 2020, 8:10 a.m.
Plz try to update the questions from recent years too. Good questions. Thank you
Abc
July 16, 2020, 11:47 p.m.
I want to see 2018,2019 & 2020 questions also since the pattern has been changed with the year.plz.... update as fast as possible .