JEE Main Previous Year Question of Physics with Solutions are available here. Practicing JEE Main Previous Year Papers Questions of Physics will help all the JEE aspirants in realizing the question pattern as well as help in analyzing their weak & strong areas.
Get detailed Class 11th &12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Simulator
Previous Years AIEEE/JEE Mains Questions
Q. In an experiment the angles are required to be measured using an instrument 29 divisions of the main scale exactly coincide with the 30 divisions of the vernier scale. If the smallest division of the main scale is half-a-degree $\left(=0.5^{\circ}\right)$, then the least count of the instrument is :-
(1) One degree
(2) Half degree
(3) One minute
(4) Half minute
[AIEEE - 2009]
Ans. (3)
Least count of vernier callipers
L.C. = 1MSD – 1VSD
But here $29 \mathrm{MSD}=30 \mathrm{VSD} \Rightarrow 1 \mathrm{VSD}=\frac{29}{30} \mathrm{MSD}$
$\Rightarrow \mathrm{L.C.}=1 \mathrm{MSD}-\frac{29}{30} \mathrm{MSD}=$
$\frac{1}{30} \mathrm{MSD}=\frac{1}{30} \times 0.5^{\circ}=\left(\frac{1}{60}\right)^{\circ}=1$ minute.
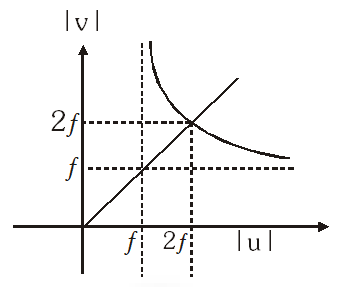
Q. In an optics experiment, with the position of the object fixed, a student varies the position of a convex lens and for each position, the screen is adjusted to get a clear image of the object. A graph between the object distance u and the image distance v, from the lens, is plotted using the same scale for the two axes. A straight line passing through the origin and making an angle of $45^{\circ}$ with the x-axis meets the experimental curve at P. The coordinates of P will be :-
(1) (ƒ, ƒ)
(2) (4ƒ, 4ƒ)
(3) (2ƒ, 2ƒ)
(4) $\left(\frac{f}{2}, \frac{f}{2}\right)$
[AIEEE - 2009]
Ans. (3)

Q. The respective number of significant figures for the numbers $23.023,0.0003$ and $2.1 \times 10^{-3}$ are :-
(1) 4, 4, 2 (2) 5, 1, 2 (3) 5, 1, 5 (4) 5, 5, 2
[AIEEE - 2010]
Ans. (2)
5, 1, 2 resp.
Q. A screw gauge gives the following reading when used to measure the diameter of a wire.
Main scale reading : 0 mm.
Circular scale reading : 52 divisions
Given that 1 mm on main scale corresponds to 100 divisions of the circular scale.
The diameter of wire from the above date is :-
(1) 0.026 cm (2) 0.005 cm (3) 0.52 cm (4) 0.052 cm
[AIEEE - 2011]
Ans. (4)
Least count $=\frac{1 \mathrm{mm}}{100}=0.01 \mathrm{mm}$
Diameter of the wire = 0 + 52 × 0.01 mm = 0.52 mm = 0.052 cm
Q. A spectrometer gives the following reading when used to measure the angle of a prism. Main scale reading : 58.5 degree Vernier scale reading : 09 divisions Given that 1 division on main scale corresponds to 0.5 degree. Total divisions on the vernier scale is 30 and match with 29 divisions of the main scale. The angle of the prism from the above data :
(1) 59 degree (2) 58.59 degree (3) 58.77 degree (4) 58.65 degree
[AIEEE - 2012]
Ans. (4)
Least count = MSD – VSD
where $\mathrm{MSD}=0.5^{\circ} \& 30 \mathrm{VSD}=29 \mathrm{MSD}$
so least count $=0.5^{\circ}-\left(\frac{29}{30}\right) \times 0.5^{\circ}=\left(\frac{0.5}{30}\right)^{\circ}$
Reading $=58.5^{\circ}+(09) \times\left(\frac{0.5}{30}\right)^{\circ}=58.65^{\circ}$
Q. Resistance of a given wire is obtained by measuring the current flowing in it and the voltage difference applied across it. If the percentage errors in the measurement of the current and the voltage difference are 3% each, then error in the value of resistance of the wire is :-
(1) 3% (2) 6% (3) zero (4) 1%
[AIEEE - 2012]
Ans. (2)
$\mathrm{R}=\frac{\mathrm{V}}{\mathrm{I}} \Rightarrow \frac{\Delta \mathrm{R}}{\mathrm{R}}=\pm\left(\frac{\Delta \mathrm{V}}{\mathrm{V}}+\frac{\Delta \mathrm{I}}{\mathrm{I}}\right)$
$=\pm(3+3) \%=\pm 6 \%$
Q. The current voltage relation of diode is given by $\mathrm{I}=\left(\mathrm{e}^{1000 \mathrm{V} / \mathrm{T}}-1\right) \mathrm{mA}$, where the applied voltage V is in volts and the temperature T is in degree Kelvin. If a student makes an error measuring $\pm 0.01 \mathrm{V}$ while measuring the current of 5 mA at 300 K, what will be error in the value of current in mA ?
(1) 0.5 mA (2) 0.05 mA (3) 0.2 mA (4) 0.02 mA
[JEE-Mains 2014]
Ans. (3)
Given current $\mathrm{I}=\left(e^{1000 \mathrm{V} / \mathrm{T}}-1\right) \mathrm{mA}$
$\Rightarrow \mathrm{I}+1=e^{1000 \mathrm{V} / \mathrm{T}}$
$\mathrm{d} \mathrm{l}=\frac{1000}{\mathrm{T}}\left[e^{\frac{1000 \mathrm{v}}{\mathrm{T}}}\right] \mathrm{d} \mathrm{V}$
$\mathrm{d} \mathrm{l}=\frac{1000}{\mathrm{T}}[1+1] \mathrm{dV}=\frac{1000}{300}[6] \times(0.01)$
dI = 0.2 mA
Q. A student measured the length of a rod and wrote it as 3.50 cm. Which instrument did he use to measure it ?
(1) A screw gauge having 100 divisions in the circular scale and pitch as 1 mm.
(2) A screw gauge having 50 divisions in the circular scale and pitch as 1 mm.
(3) A meter scale
(4) A vernier calliper where the 10 divisions in vernier scale matches with 9 division in main scale and main scale has 10 divisions in 1 cm.
[JEE-Mains 2014]
Ans. (4)
Least count of varnier calliper is 0.01 cm
Hence it matches with the reading.
Q. The period of oscillation of a simple pendulum is T = $2 \pi \sqrt{\frac{\mathrm{L}}{\mathrm{g}}}$. Measured value of L is 20.0 cm known to 1 mm accuracy and time for 100 oscillations of the pendulum is found to be 90s using a wrist watch of 1s resolution. The accuracy in the determination of g is :
(1)1% (2) 5% (3) 2% (4) 3%
[JEE-Mains 2015]
Ans. (4)
$\mathrm{T}=2 \pi \sqrt{\frac{\ell}{\mathrm{g}}}$
$\mathrm{g}=\frac{4 \pi^{2} \ell}{\mathrm{T}^{2}}$
$\frac{\Delta \mathrm{g}}{\mathrm{g}}=\frac{\Delta \ell}{\ell}+2 \frac{\Delta \mathrm{T}}{\mathrm{T}}$
$\frac{\Delta \mathrm{g}}{\mathrm{g}}=\frac{1 \times 10^{-3}}{20 \times 10^{-2}}+2 \times \frac{1}{100 \times \frac{90}{100}}$
$\therefore \frac{\Delta \mathrm{g}}{\mathrm{g}} \times 100=2.722 \% \approx 3 \%$
Q. A screw gauge with a pitch of 0.5 mm and a circular scale with 50 divisions is used to measure the thickness of a thin sheet of Aluminium. Before starting the measurement , it is found that when the two jaws of the screw gauge are brought in contact, the 45th division coincides with the main scale line and that the zero of the main scale is barely visible. What is the thickness of the sheet if the main scale reading is 0.5 mm and the 25th division coincides with the main scale line ?
(1) 0.50 mm (2) 0.75 mm (3) 0.80 mm (4) 0.70 mm
[JEE-Mains 2016]
Ans. (3)


Q. A student measures the time period of 100 oscillations of a simple pendulum four times. The data set is 90 s, 91 s, 95 s and 92 s. If the minimum division in the measuring clock is 1 s, then the reported mean time should be :-
(1) $92 \pm 3 \mathrm{s}$
(2) $92 \pm 2 \mathrm{s}$
(3) $92 \pm 5.0 \mathrm{s}$
(4) $92 \pm 1.8 \mathrm{s}$
[JEE-Mains 2016]
Ans. (2)
$\mathrm{T}_{\mathrm{AV}}=92 \mathrm{s}$
$(|\Delta \mathrm{T}|)_{\text {mean }}=1.5 \mathrm{s}$
Least conunt of clock is 1sec. So value that clock can measure should be 1, 2, 3......so on
so reported mean time should be
$92 \pm 2$
Ref : NCERT (XIth) Ex. 2.7, Page. 25
Q. The following observations were taken for determining surface tensiton T of water by capillary method :
Diameter of capilary, $\mathrm{D}=1.25 \times 10^{-2} \mathrm{m}$
rise of water, $h=1.45 \times 10^{-2} \mathrm{m}$
Using $\mathrm{g}=9.80 \mathrm{m} / \mathrm{s}^{2}$ and the simplified relation
$\mathrm{T}=\frac{\mathrm{rhg}}{2} \times 10^{3} \mathrm{N} / \mathrm{m},$ the possible error in surface tension is closest to :
(1) 2.4% (2) 10% (3) 0.15% (4) 1.5%
[JEE-Mains 2017]
Ans. (4)
$\mathrm{T}=\frac{\mathrm{rhg}}{2} \times 10^{3}$
$\frac{\Delta \mathrm{T}}{\mathrm{T}}=\frac{\Delta \mathrm{r}}{\mathrm{r}}+\frac{\Delta \mathrm{h}}{\mathrm{h}}+0$
$100 \times \frac{\Delta \mathrm{T}}{\mathrm{T}}=\left(\frac{10^{-2} \times .01}{1.25 \times 10^{-2}}+\frac{10^{-2} \times .01}{1.45 \times 10^{-2}}\right) 100$
$=(0.8+0.689)$
$=(1.489)$
$100 \times \frac{\Delta \mathrm{T}}{\mathrm{T}}=1.489 \%$
= 1.5%
Q. The density of a material in the shape of a cube is determined by measuring three sides of the cube and its mass. If the relative errors in measuring the mass and length are respectively 1.5% and 1%, the maximum error in determining the density is :-
(1) 3.5 % (2) 4.5 % (3) 6 % (4) 2.5 %
[JEE-Mains 2018]
Ans. (2)
Density $=\frac{\text { Mass }}{\text { Volume }}$
$\frac{1 \Delta \mathrm{d}}{\mathrm{d}}=\frac{1 \Delta \mathrm{M}}{\mathrm{M}}+\frac{3 \Delta \mathrm{L}}{\mathrm{L}}$
= 1.5 + 3(1)
= 4.5 %
Comments
rjrjrj
Jan. 29, 2021, 9:57 p.m.
noiceeeeeee.....dhrjksbsksh झींगुर giving जड़ित ju युग झिझक झुग्गी जग जगत जूजू जगत कठिन जयजयवंती पीएसएलवी পদস্থ paid डूबी कब hdksk jsjs
