JEE Main Previous Year Question of Physics with Solutions are available here. Practicing JEE Main Previous Year Papers Questions of Physics will help all the JEE aspirants in realizing the question pattern as well as help in analyzing their weak & strong areas.
Get detailed Class 11th &12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Q. A ball is made of a material of density r where $\rho_{\text {oil }}<\rho<\rho_{\text {water }}$ with $\rho_{\text {oil }}$ and $\rho_{\text {water }}$ representing the densities of oil and water, respectively. The oil and water are immiscible. If the above ball is in equilibrium in a mixture of this oil and water, which of the following pictures represents its equilibrium position ?
[AIEEE-2010]
[AIEEE-2010]
Ans. (3)
In equilibrium ball will remain at the interface of water and oil.
Q. Water is flowing continuously from a tap having an internal diameter $8 \times 10^{-3}$m. The water velocity as it leaves the tap is 0.4 ms–1. The diameter of the water stream at a distance $2 \times 10^{-1}$m below the tap is close to :-
(1) $9.6 \times 10^{-3} \mathrm{m}$
(2) $3.6 \times 10^{-3} \mathrm{m}$
(3) $5.0 \times 10^{-3} \mathrm{m}$
(4) $7.5 \times 10^{-3} \mathrm{m}$
[AIEEE-2011]
Ans. (2)
According to equation of continuity
$\mathrm{A}_{1} \mathrm{V}_{1}=\mathrm{A}_{2} \mathrm{V}_{2}$ or $\mathrm{r}_{2}=\sqrt{\frac{\mathrm{r}_{1}^{2} \mathrm{v}_{1}}{\mathrm{v}_{2}}}$
Velocity of stream at 0.2 m below tap.
$\mathrm{V}_{2}^{2}=\mathrm{V}_{1}^{2}+2 \mathrm{as}=0.16+2 \times 10 \times 0.2=4.16 \mathrm{m} / \mathrm{s}$
$\mathrm{r}_{2}=\sqrt{\frac{\mathrm{r}_{1}^{2} \mathrm{v}_{1}}{\mathrm{v}_{2}}}=\sqrt{\frac{16 \times 10^{-6} \times 0.4}{2}}=\sqrt{3.2} \times 10^{-3} \mathrm{m}$
so diameter $=2 \times \sqrt{3.2} \times 10^{-3} \mathrm{m}$
$=2 \times 1.8 \times 10^{-3}=3.6 \times 10^{-3} \mathrm{m}$
Q. Work done in increasing the size of a soap bubble from a radius of 3 cm to 5cm is nearly (Surface tension of soap solution = 0.03 Nm–1) :-
(1) $2 \pi \mathrm{mJ}$
(2) $0.4 \pi \mathrm{mJ}$
(3) $4 \pi \mathrm{mJ}$
(4) $0.2 \pi \mathrm{mJ}$
[AIEEE-2011]
Ans. (2)
$\mathrm{W}=8 \pi \mathrm{T}\left[\left(\mathrm{r}_{2}^{2}\right)-\left(\mathrm{r}_{1}^{2}\right)\right]$
$=8 \times \pi \times 0.03[25-9] \times 10^{-4}$
$=\pi \times 0.24 \times 16 \times 10^{-4}$
$=3.8 \times 10^{-4} \pi$
$=0.384 \pi \mathrm{m} \mathrm{J} \approx 0.4 \pi \mathrm{mJ}$
Q. Two merucry drops (each of radius 'r') merge to form a bigger drop. The surface energy of the bigger drop, ifs T is the surface tension, is :
(1) $2^{5 / 3} \pi r^{2} T$
(2) $4 \pi r^{2} \mathrm{T}$
(3) $2 \pi r^{2} T$
(4) $2^{8 / 3} \pi r^{2} \mathrm{T}$
[AIEEE-2011]
Ans. (4)
By volume conservation
$\frac{4}{3} \pi \mathrm{R}^{3}=2\left(\frac{4}{3} \pi \mathrm{r}^{3}\right)$
$\mathrm{R}=2^{1 / 3} \mathrm{r}$
Surface energy E = T (A)
$=\mathrm{T}\left(4 \pi \mathrm{R}^{2}\right)=\mathrm{T}\left(4 \pi 2^{2 / 3} \mathrm{r}^{2}\right)=2^{8 / 3} \pi \mathrm{r}^{2} \mathrm{T}$
Q. If a ball of steel (density $\left.\rho=7.8 \mathrm{g} \mathrm{cm}^{-3}\right)$ attains a terminal velocity of 10 cm s–1 when falling
in a tank of water (coefficient of viscosity $\left.\eta_{\text {water }}=8.5 \times 10^{-4} \mathrm{Pa.s}\right)$ then its terminal velocity in glycerine $\left(\rho=1.2 \mathrm{g} \mathrm{cm}^{-3}, \eta=13.2 \mathrm{Pa.s}\right)$ would be nearly :-
(1) $1.6 \times 10^{-5} \mathrm{cm} \mathrm{s}^{-1}$
(2) $6.25 \times 10^{-4} \mathrm{cm} \mathrm{s}^{-1}$
(3) $6.45 \times 10^{-4} \mathrm{cm} \mathrm{s}^{-1}$
(4) $1.5 \times 10^{-5} \mathrm{cm} \mathrm{s}^{-1}$
[AIEEE-2011]
Ans. (2)
Terminal velocity $\mathrm{V}_{\infty} \frac{\mathrm{d}_{\mathrm{b}}-\mathrm{d}_{\ell}}{\eta}$
$\frac{V_{1}}{V_{2}}=\frac{7.8-1}{8.5 \times 10^{-4}} \times \frac{13.2}{7.8-1.2}$
$\frac{10}{\mathrm{V}_{2}}=1.6 \times 10^{4}$
$\mathrm{V}_{2}=\frac{10}{1.6 \times 10^{4}}=6.25 \times 10^{-4}$
Q. A wooden cube (density of wood 'd') of side '$\ell$' floats in a liquid of density 'r' with its upper and lower surfaces horizontal. If the cube is pushed slightly down and released, it performs simple harmonic motion of period 'T'. Then, 'T' is equal to :-
(1) $2 \pi \sqrt{\frac{\ell \rho}{(\rho-\mathrm{d}) \mathrm{g}}}$
(2) $2 \pi \sqrt{\frac{\ell \mathrm{d}}{\rho \mathrm{g}}}$
(3) $2 \pi \sqrt{\frac{\ell \rho}{\mathrm{dg}}}$
(4) $2 \pi \sqrt{\frac{\ell \mathrm{d}}{(\rho-\mathrm{d}) \mathrm{g}}}$
[AIEEE-2011]
Ans. (2)
By using $\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{m}}{\mathrm{A} \rho \mathrm{g}}}$
Where $\mathrm{m}=\ell^{3} \mathrm{d}$ and $\mathrm{A}=\ell^{2}$
$\mathrm{T}=2 \pi \sqrt{\frac{\ell^{3} \mathrm{d}}{\ell^{2} \rho \mathrm{g}}} \Rightarrow \mathrm{T}=2 \pi \sqrt{\frac{\ell \mathrm{d}}{\rho \mathrm{g}}}$
Q. A thin liquid film formed between a U-shaped wire and a light slider supports a weight of $1.5 \times 10^{-2} \mathrm{N}$ (see figure). The length of the slider is 30 cm and its weight negligible. The surface tension of the liquid film is :-
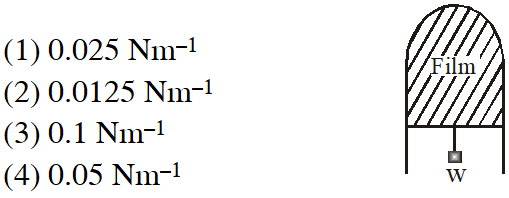[AIEEE-2012]
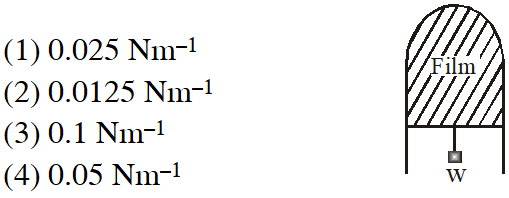[AIEEE-2012]
Ans. (2)
weight $=\mathrm{mg}=1.5 \times 10^{-2} \mathrm{N}(\text { given })$
length $=\ell=30 \mathrm{cm}(\text { given })$
= 0.3 m
$2 \mathrm{T} \ell=\mathrm{mg}$
$\mathrm{T}=\frac{\mathrm{mg}}{2 \ell}=\frac{1.5 \times 10^{-2}}{2 \times 0.3}=0.025 \mathrm{N} / \mathrm{m}$
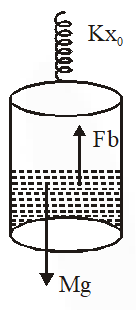
Q. A uniform cylinder of length L and mass M having cross- sectional area A is suspended, with its length vertical, form a fixed point by a massless spring, such that it is half submerged in a liquid of density $\sigma$ at equilibrium position. The extension $\mathrm{X}_{0}$ of the spring when it is in equilibrium is :
(1) $\frac{\mathrm{Mg}}{\mathrm{k}}$
( 2)$\frac{\mathrm{Mg}}{\mathrm{k}}\left(1-\frac{\mathrm{LA\sigma}}{\mathrm{M}}\right)$
(3) $\frac{\mathrm{Mg}}{\mathrm{k}}\left(1-\frac{\mathrm{LA\sigma}}{2 \mathrm{M}}\right)$
(4)$\frac{\mathrm{Mg}}{\mathrm{k}}\left(1+\frac{\mathrm{LA\sigma}}{\mathrm{M}}\right)$
(Here k is spring constant)
[AIEEE-2013]
Ans. (1)
At equilibrium
$\mathrm{Kx}_{0}=\mathrm{Mg}-\mathrm{B}$
$\mathrm{Kx}_{0}=\mathrm{Mg}-\frac{\sigma \mathrm{AL}}{2}$
$\mathrm{X}_{0}=\frac{\left(\mathrm{Mg}-\frac{\sigma \mathrm{AL}}{2} \mathrm{g}\right)}{\mathrm{K}}$
$=\left[1-\frac{\sigma \mathrm{AL}}{2 \mathrm{M}}\right]$
.
Q. Assume that a drop of liquid evaporates by decrease in its surface energy, so that its temperature remains unchanged. What should be the minimum radius of the drop for this to be possible? The surface tension is T, density of liquid is and L is its latent heat of vaporization.
(1) $\frac{\rho \mathrm{L}}{\mathrm{T}}$
(2) $\sqrt{\frac{\mathrm{T}}{\rho \mathrm{L}}}$
( 3)$\frac{\mathrm{T}}{\rho \mathrm{L}}$
(4) $\frac{2 \mathrm{T}}{\rho \mathrm{L}}$
[AIEEE-2013]
Ans. (3)
If a layer of thickness dr is evaporates then change in surface energy
= (change in surface area) T
$=\left(\mathrm{d}\left(4 \pi \mathrm{r}^{2}\right)\right) \mathrm{T}=8 \pi \mathrm{rdr} \mathrm{T}$
energy required to evaporate layer of thickness dr $=\left(4 \mathrm{pr}^{2} \mathrm{dr}\right) \rho . \mathrm{L}$
The process of evaporation only starts only if change in surface energy is just sufficient to evaporate the water layer
$\Rightarrow\left(4 \pi r^{2} d r\right) L \rho=(8 \pi r d r) T$
$\Rightarrow \mathrm{r}=\frac{2 \pi}{\rho \mathrm{L}}$
Q. On heating water, bubbles being formed at the bottom of the vessel detatch
and rise. Take the bubbles to be spheres of radius R and making a circular contact of radius r with the bottom of the vessel. If r << R, and the surface tension of water is T, value of r just before bubbles detatch is:-
(dencity of water is $\rho_{\mathrm{w}}$)
(1) $\mathrm{R}^{2} \sqrt{\frac{\rho_{\mathrm{w}} \mathrm{g}}{\mathrm{T}}}$
(2) $\mathrm{R}^{2} \sqrt{\frac{3 \rho_{\mathrm{w}} \mathrm{g}}{\mathrm{T}}}$
(3) $\mathrm{R}^{2} \sqrt{\frac{\rho_{\mathrm{w}} \mathrm{g}}{3 \mathrm{T}}}$
(4) $\mathrm{R}^{2} \sqrt{\frac{\rho_{\mathrm{w}} \mathrm{g}}{6 \mathrm{T}}}$
[JEE Mains-2014]
Ans. (4)
Force due to Surface Tenstion
$=\mathrm{T}(2 \pi \mathrm{r}) \sin \theta=\mathrm{T}(2 \pi \mathrm{r}) \times \frac{\mathrm{r}}{\mathrm{R}}$
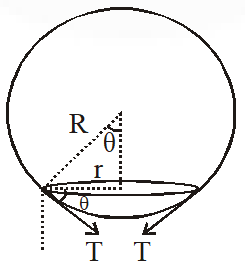This force will balance the force of Bouyancy
$\mathrm{T}(2 \pi \mathrm{r}) \times \frac{\mathrm{r}}{\mathrm{R}}=\rho_{\mathrm{w}} \times \frac{4}{3} \pi \mathrm{R}^{3} \mathrm{g}$
$r=R^{2} \sqrt{\frac{2 \rho_{\mathrm{w}} g}{3 T}}$
This force will balance the force of Bouyancy
$\mathrm{T}(2 \pi \mathrm{r}) \times \frac{\mathrm{r}}{\mathrm{R}}=\rho_{\mathrm{w}} \times \frac{4}{3} \pi \mathrm{R}^{3} \mathrm{g}$
$r=R^{2} \sqrt{\frac{2 \rho_{\mathrm{w}} g}{3 T}}$
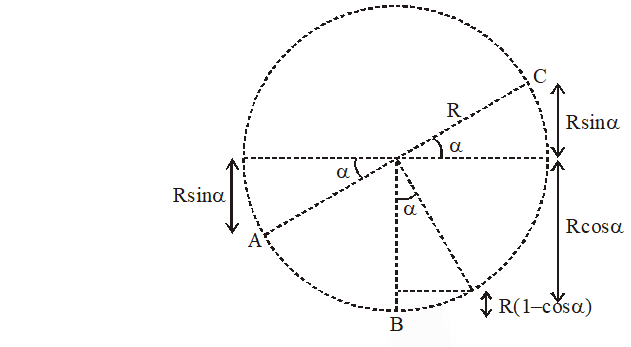
Q. There is a circular tube in a vertical plane. Two liquids which do not mix and of densities $\mathrm{d}_{1}$ and $\mathrm{d}_{2}$ are filled in the tube. Each liquid subtends $90^{\circ}$ angle at centre. Radius joining their interface makes an angle with vertical. Ratio $\frac{\mathrm{d}_{1}}{\mathrm{d}_{2}}$ is :
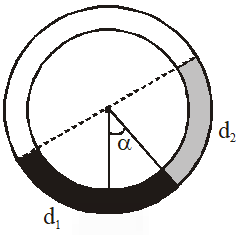
[JEE Mains-2014]
[JEE Mains-2014]
Ans. (1)
Let Radius of circular tube is R
