JEE Main Previous Year Question of Physics with Solutions are available here. Practicing JEE Main Previous Year Papers Questions of Physics will help all the JEE aspirants in realizing the question pattern as well as help in analyzing their weak & strong areas.
Get detailed Class 11th &12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Simulator
Previous Years AIEEE/JEE Mains Questions
Q. The height at which the acceleration due to gravity becomes $\frac{g}{9}$ (where g = the acceleration due to gravity on the surface of the earth) in terms of R, the radius of the earth, is :-
(1) $\frac{\mathrm{R}} {2}$ (2) $\sqrt{2} \mathrm{R}$ (3) 2R (4) $\frac{\mathrm{R}}{\sqrt{2}}$
[AIEEE - 2009]
Ans. (3)
$\mathrm{g}_{\mathrm{h}}=\frac{\mathrm{g}}{\left(1+\frac{\mathrm{h}}{\mathrm{R}}\right)^{2}} \Rightarrow\left(1+\frac{\mathrm{h}}{\mathrm{R}}\right)^{2}=\frac{\mathrm{g}}{\mathrm{g}_{\mathrm{h}}}=9$
$\Rightarrow 1+\frac{\mathrm{h}}{\mathrm{R}}=3 \Rightarrow \mathrm{h}=2 \mathrm{R}$
Q. Two bodies of masses m and 4m are placed at a distance r. The gravitational potential at a point on the line joining them where the gravitational field is zero is :-
$(1)-\frac{6 \mathrm{Gm}}{\mathrm{r}}$
$(2)-\frac{9 \mathrm{Gm}}{\mathrm{r}}$
(3) zero
$(4)-\frac{4 \mathrm{Gm}}{\mathrm{r}}$
[AIEEE - 2011]
Ans. (2)
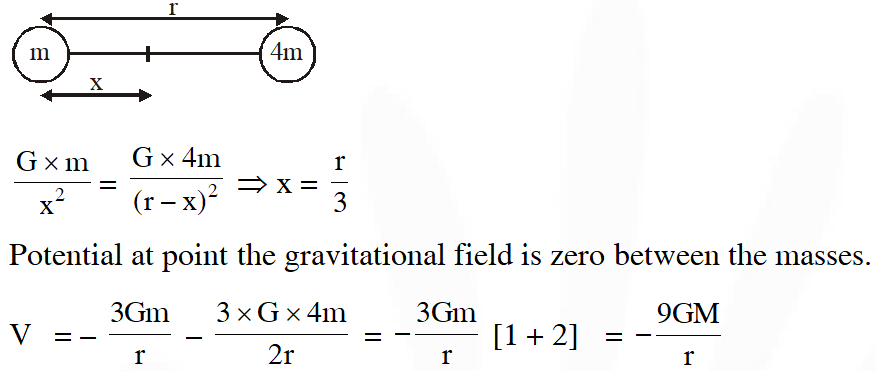
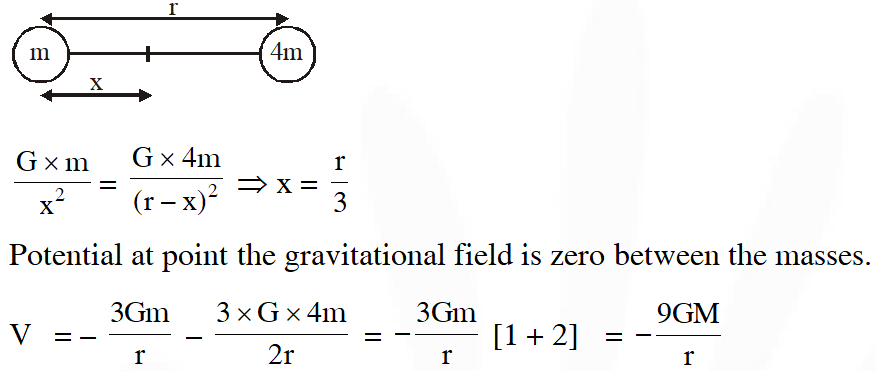
Q. Two particles of equal mass 'm' go around a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle with respect to their centre of mass is:-
(1) $\sqrt{\frac{\mathrm{Gm}}{\mathrm{R}}}$ (2) $\sqrt{\frac{\mathrm{Gm}}{4 \mathrm{R}}}$ (3) $\sqrt{\frac{\mathrm{Gm}}{3 \mathrm{R}}}$ (4) $\sqrt{\frac{\mathrm{Gm}}{2 \mathrm{R}}}$
[AIEEE-2011]
Ans. (2)
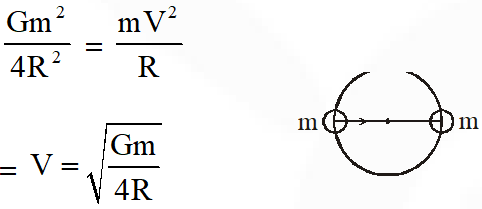
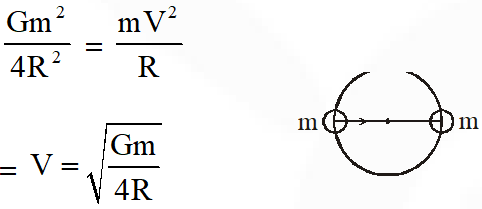
Q. The mass of a spaceship is 1000 kg. It is to be launched from the earth's surface out into free space. The value of 'g' and 'R' (radius of earth) are 10 m/s2 and 6400 km respectively. The required energy for this work will be :-
(1) $6.4 \times 10^{10}$ Joules
(2) $6.4 \times 10^{11}$ Joules
(3) $6.4 \times 10^{8}$ Joules
(4) $6.4 \times 10^{9}$ Joules
[AIEEE-2012]
Ans. (1)
$\mathrm{PE}_{\mathrm{i}}+\mathrm{KE}_{\mathrm{i}}=\mathrm{PE}_{\mathrm{f}}+\mathrm{KE}_{\mathrm{f}}$
$-\mathrm{mgR}+\mathrm{KE}_{\mathrm{i}}=0+0$
$\mathrm{KE}_{\mathrm{i}}=+\mathrm{mgR}=1000 \times 10 \times 6.4 \times 10^{6}$
work done $=6.4 \times 10^{10} \mathrm{J}$
Q. What is the minimum energy required to launch a satellite of mass m from the surface of a planet of mass M and radius R in a circular orbit at an altitude of 2R ?
(1) $\frac{5 \mathrm{GmM}}{6 \mathrm{R}}$ (2) $\frac{2 \mathrm{GmM}}{3 \mathrm{R}}$ (3) $\frac{\mathrm{GmM}}{2 \mathrm{R}}$ (4) $\frac{\mathrm{GmM}}{3 \mathrm{R}}$
[JEE-Mains 2013]
Ans. (1)
From energy conservation
$\frac{\mathrm{GMm}}{\mathrm{R}}+\mathrm{KE}=\frac{-\mathrm{GMm}}{3 \mathrm{R}}+\frac{1}{2} \mathrm{mV}^{2} \ldots(\mathrm{i})$ ...(i)
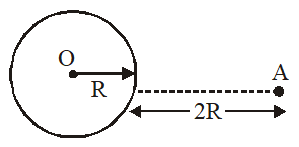From force balance at A,
$\frac{\mathrm{GMm}}{(3 \mathrm{R})^{2}}=\frac{\mathrm{mv}^{2}}{3 \mathrm{R}} \Rightarrow \mathrm{V}^{2}=\frac{\mathrm{GM}}{3 \mathrm{R}}$ ...........(ii)
from (i) & (ii)
$\mathrm{KE}_{\text {suface }}=\frac{5}{6} \frac{\mathrm{GMm}}{\mathrm{R}}$
From force balance at A,
$\frac{\mathrm{GMm}}{(3 \mathrm{R})^{2}}=\frac{\mathrm{mv}^{2}}{3 \mathrm{R}} \Rightarrow \mathrm{V}^{2}=\frac{\mathrm{GM}}{3 \mathrm{R}}$ ...........(ii)
from (i) & (ii)
$\mathrm{KE}_{\text {suface }}=\frac{5}{6} \frac{\mathrm{GMm}}{\mathrm{R}}$
Q. Four particles, each of mass M and equidistant from each other, move along a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is :
(1) $\sqrt{\frac{\mathrm{GM}}{\mathrm{R}}(1+2 \sqrt{2})}$
(2) $\frac{1}{2} \sqrt{\frac{\mathrm{GM}}{\mathrm{R}}(1+2 \sqrt{2})}$
(3) $\sqrt{\frac{\mathrm{GM}}{\mathrm{R}}}$
(4) $\sqrt{2 \sqrt{2} \frac{\mathrm{GM}}{\mathrm{R}}}$
[JEE-Mains 2014]
Ans. (2)
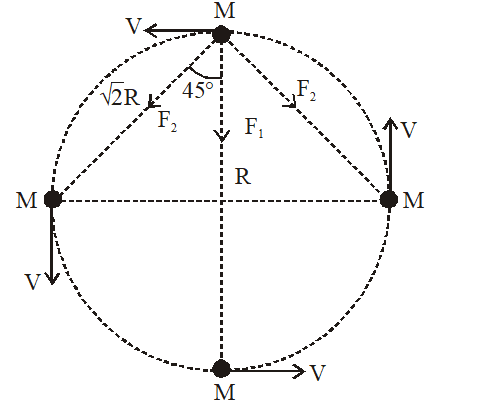Net force on one particle
$\mathrm{F}_{\mathrm{net}}=\mathrm{F}_{1}+2 \mathrm{F}_{2} \cos 45^{\circ}=$ Centripetal force
$\Rightarrow \frac{\mathrm{GM}^{2}}{(2 \mathrm{R})^{2}}+\left[\frac{2 \mathrm{GM}^{2}}{(\sqrt{2} \mathrm{R})^{2}} \cos 45^{\circ}\right]=\frac{\mathrm{MV}^{2}}{\mathrm{R}}$
$\mathrm{V}=\frac{1}{2} \sqrt{\frac{\mathrm{GM}}{\mathrm{R}}(1+2 \sqrt{2})}$
$\mathrm{V}=-\frac{\mathrm{GM}}{2 \mathrm{R}^{3}}\left[3 \mathrm{R}^{2}-\frac{\mathrm{R}^{2}}{4}\right]+\frac{3 \mathrm{G}}{2} \frac{\mathrm{M}}{8 \frac{\mathrm{R}}{2}}$
$=\frac{-11 \mathrm{GM}}{8 \mathrm{R}}+\frac{3 \mathrm{GM}}{8 \mathrm{R}}=-\frac{\mathrm{GM}}{\mathrm{R}}$
Net force on one particle
$\mathrm{F}_{\mathrm{net}}=\mathrm{F}_{1}+2 \mathrm{F}_{2} \cos 45^{\circ}=$ Centripetal force
$\Rightarrow \frac{\mathrm{GM}^{2}}{(2 \mathrm{R})^{2}}+\left[\frac{2 \mathrm{GM}^{2}}{(\sqrt{2} \mathrm{R})^{2}} \cos 45^{\circ}\right]=\frac{\mathrm{MV}^{2}}{\mathrm{R}}$
$\mathrm{V}=\frac{1}{2} \sqrt{\frac{\mathrm{GM}}{\mathrm{R}}(1+2 \sqrt{2})}$
$\mathrm{V}=-\frac{\mathrm{GM}}{2 \mathrm{R}^{3}}\left[3 \mathrm{R}^{2}-\frac{\mathrm{R}^{2}}{4}\right]+\frac{3 \mathrm{G}}{2} \frac{\mathrm{M}}{8 \frac{\mathrm{R}}{2}}$
$=\frac{-11 \mathrm{GM}}{8 \mathrm{R}}+\frac{3 \mathrm{GM}}{8 \mathrm{R}}=-\frac{\mathrm{GM}}{\mathrm{R}}$
Q. From a solid sphere of mass M and radius R, a spherical portion of radius $\frac{\mathrm{R}}{2}$ is removed, as shown in the figure. Taking gravitational potential V = 0 at r = $\infty$, the potential at the centre of the cavity thus formed is : (G = gravitational constant)
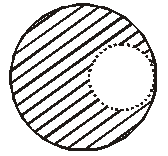(1) $\frac{-2 \mathrm{GM}}{3 \mathrm{R}}$
(2) $\frac{-2 \mathrm{GM}}{\mathrm{R}}$
(3) $\frac{-\mathrm{GM}}{2 \mathrm{R}}$
(4) $\frac{-\mathrm{GM}}{\mathrm{R}}$
[JEE-Mains 2015]
(1) $\frac{-2 \mathrm{GM}}{3 \mathrm{R}}$
(2) $\frac{-2 \mathrm{GM}}{\mathrm{R}}$
(3) $\frac{-\mathrm{GM}}{2 \mathrm{R}}$
(4) $\frac{-\mathrm{GM}}{\mathrm{R}}$
[JEE-Mains 2015]
Ans. (4)
By principle of superosition
$\mathrm{V}=-\frac{\mathrm{GM}}{2 \mathrm{R}^{3}}\left[3 \mathrm{R}^{2}-\frac{\mathrm{R}^{2}}{4}\right]+\frac{3 \mathrm{G}}{2} \frac{\mathrm{M}}{8 \frac{\mathrm{R}}{2}}$
$=\frac{-11 \mathrm{GM}}{8 \mathrm{R}}+\frac{3 \mathrm{GM}}{8 \mathrm{R}}=-\frac{\mathrm{GM}}{\mathrm{R}}$
Q. A satellite is reolving in a circular orbit at a height 'h' from the earth's surface (radius of earth R ; h << R). The minimum increase in its orbital velocity required, so that the satellite could escape from the earth's gravitational field, is close to : (Neglect the effect of atmosphere).
(1) $\sqrt{\mathrm{gR}}(\sqrt{2}-1)$
(2) $\sqrt{2 \mathrm{gR}}$
(3) $\sqrt{\mathrm{gR}}$
(4) $\sqrt{\mathrm{gR} / 2}$
[JEE-Mains 2016]
Ans. (1)
$\mathrm{V}_{0}=\sqrt{\frac{\mathrm{GM}}{\mathrm{R}}}$ or $\sqrt{\mathrm{gR}}$
$\mathrm{V}_{\mathrm{e}} \sqrt{\frac{2 \mathrm{GM}}{\mathrm{R}}}$ or $\sqrt{2 \mathrm{gR}}$
$\therefore$ Increase in velocity $=\sqrt{\mathrm{gR}}[\sqrt{2}-1]$
Q. The variation of acceleration due to gravity g with distance d from centre of the earth is best represented by (R = Earth's radius) :-
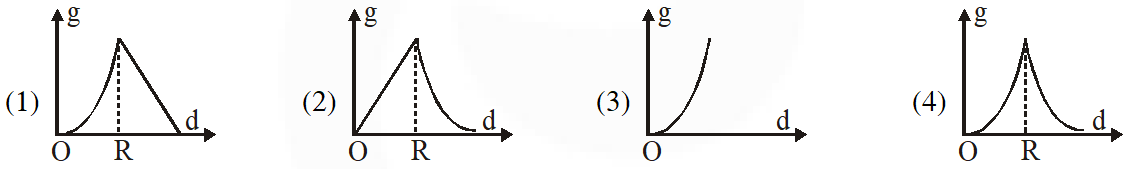[JEE-Mains 2017]
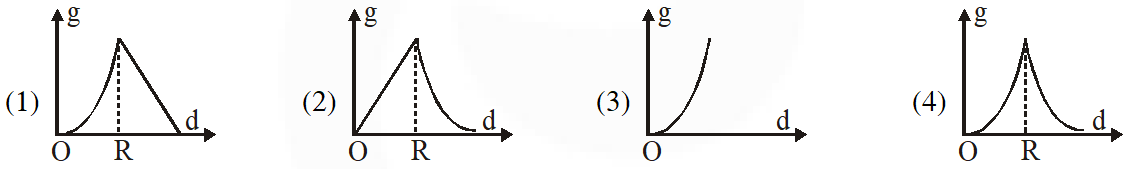[JEE-Mains 2017]
Ans. (2)
$\mathrm{g}=\frac{\mathrm{GMx}}{\mathrm{R}^{3}}$ inside the Earth (straight line)
$\mathrm{g}=\frac{\mathrm{GM}}{\mathrm{r}^{2}}$ outside the Earth
where M is Mass of Earth
option (2)
option (2)
Comments
nhà cái casino fb88
Dec. 2, 2022, 12:12 p.m.
lúc chơi những trò chơi casino trực tuyến tại nhà cái casino fb88, bạn đề nghị yêu cầu nắm bắt được mục tiêu của mình. nếu chơi cho vui thì game thủ không bắt buộc phải tìm hiểu quá nhiều. Còn nếu muốn giành chiến thắng, bạn cần chú ý các kinh nghiệm chơi Bull Bull fb88 bet1 tại: https://nhacaicacuoc.com/kinh-nghiem-choi-bull-bull-fb88-hieu-qua/
driver: https://drive.google.com/drive/folders/1ePw26bg2rt85nb9gsa6NpYMFGCgaUr9g
https://nhacaicacuoc.com/casino-fb88/
w88 casino
Dec. 1, 2022, 9:30 a.m.
Để tham gia những games bài ăn tiền thật tại w88 online thì đầu tiên người chơi nên tìm một nhà cái minh bạch, uy tín và tạo 1 tài khoản tại nhà cái hợp lí đó. Hãy nhanh nhẹn tới đối với w88 live casino trực tuyến hợp pháp, minh bạch hàng đầu VN cũng như Châu Á.
driver: https://drive.google.com/drive/folders/1xhXUdMvzbZYDpLi-DNW3D3h4vItTkQUj
https://w88xin.com/casino-w88/
Nguồn: https://w88xin.com/huong-dan-cach-choi-danh-bai-w88-an-tien-de-nhat/
đánh giá w88
Nov. 21, 2022, 9:56 a.m.
Hiện nay, chúng ta lựa chọn hình thức chơi Roulette tại nhà cái trên mạng nhiều hơn là tới những sòng bài trực tiếp. Điều đó giúp chúng ta thuận tiện lúc tham gia cá độ, tiết kiệm thời gian vô cùng.
Tuy nhiên, để tránh bị lừa đảo thì khách hàng cần chọn cho mình 1 nhà cái uy tín nhất, hoạt động công khai, có giấy phép.
người chơi có thể lựa chọn w88 trực tuyến vì nhà cái này trả thưởng nhanh lẹ, kết quả đặt cược công bằng, minh bạch.
Nguồn: https://w88xin.com/chien-thuat-va-kinh-nghiem-choi-roulette-tai-w88/
Google site: https://drive.google.com/drive/folders/1xhXUdMvzbZYDpLi-DNW3D3h4vItTkQUj
https://w88xin.com/
vòng loại world cup 2022 nam mỹ
Nov. 18, 2022, 9:02 a.m.
những trò chơi dưới đây ko được tính vào tổng doanh thu đặt cược tại A – Thể Thao: Racing, Live Casino, Arcadia Gaming, Happy 5, Thể Thao Ảo, Saba.Club, Minigame, RNG Keno/Xổ Số, trò chơi Ảo https://nhacaicacuoc.com/co-bao-nhieu-doi-tuyen-nam-my-tham-du-world-cup/