JEE Main Previous Year Question of Physics with Solutions are available here. Practicing JEE Main Previous Year Papers Questions of Physics will help all the JEE aspirants in realizing the question pattern as well as help in analyzing their weak & strong areas.
Get detailed Class 11th &12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Simulator
Previous Years AIEEE/JEE Mains Questions
Q. A long metallic bar is carrying heat from one of its ends to the other end under steady-state. The variation of temperature $\theta$ along the length x of the bar from its hot end is best described by which of the following figures ?
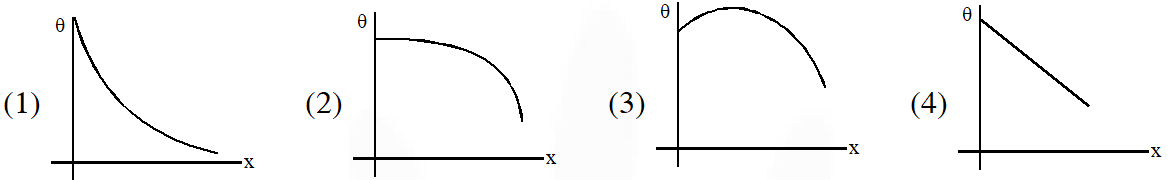[AIEEE - 2009]
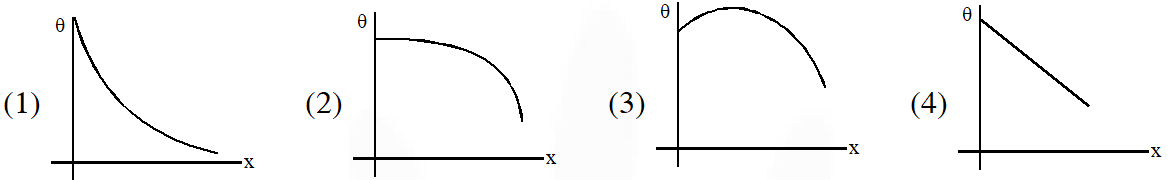[AIEEE - 2009]
Ans. (4)
The heat flow rate is given by
$\frac{d Q}{d t}=\frac{k A\left(\theta_{1}-\theta\right)}{x}$
$\Rightarrow \theta=\theta_{1}-\frac{x}{k A} \frac{d Q}{d t}$
where $\theta_{1}$ is the temp of hot end and $\theta$ is temp at a distance x from hot end.
Q. A liquid in a beaker has temperature $\theta(\mathrm{t})$ at time t and $\theta_{0}$ is temperature of surroundings, then according to Newton's law of cooling the correct graph between $\log _{\mathrm{e}}\left(\theta-\theta_{0}\right)$ and t is :-
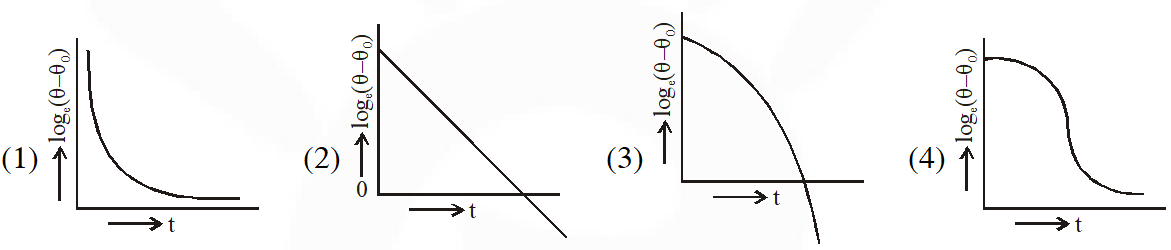[AIEEE 2012]
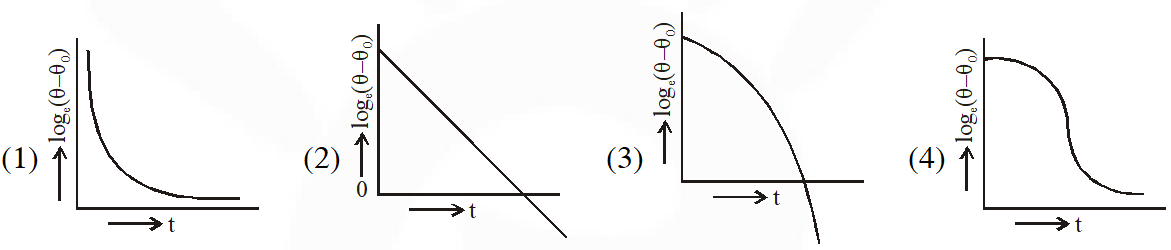[AIEEE 2012]
Ans. (2)
Newtons law of cooling
$\frac{d \theta}{d t}=-k\left(\theta-\theta_{0}\right)$
$\Rightarrow \frac{d \theta}{\left(\theta-\theta_{0}\right)}=-k d t$
Integrating
$\ln \left(\theta-\theta_{0}\right)=-k t+C$
Q. If a piece of metal is heated to temperature $\theta$ and then allowed to cool in a room which is at temperature $\theta_{0}$ the graph between the temperature T of the metal and time t will be closed to:
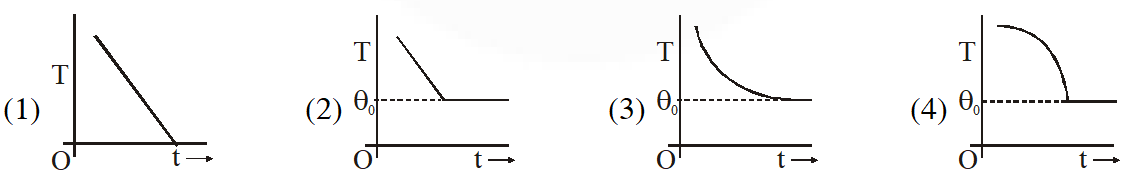[JEE-Main- 2013]
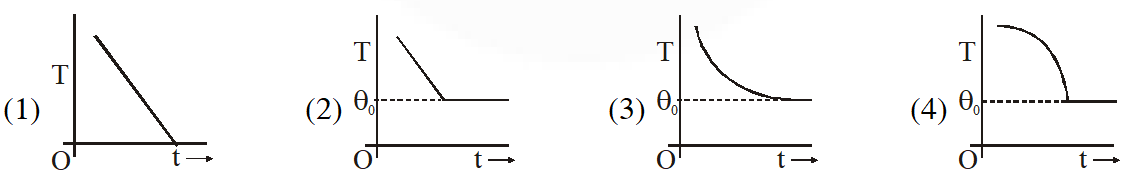[JEE-Main- 2013]
Ans. (3)
According to Newtons law of cooling, The temp goes on decreasing with time non-linearly.
Q. Three rods of Copper, Brass and Steel are welded together to form a Y-shaped structure. Area of cross-section of each rod = $4 \mathrm{cm}^{2}$. End of copper rod is maintained at $100^{\circ} \mathrm{C}$ where as ends of brass and steel are kept at $0^{\circ} \mathrm{C}$. Lengths of the copper, brass and steel rods are 46, 13 and 12 cms respectively. The rods are thermally insulated from surroundings except at ends. Thermal conductivities of copper, brass and steel are 0.92, 0.26 and 0.12 CGS units respectively. Rate of heat flow through copper rod is :
(1) 4.8 cal/s (2) 6.0 cal/s (3) 1.2 cal/s (4) 2.4 cal/s
[JEE-Main-2014]
Ans. (1)
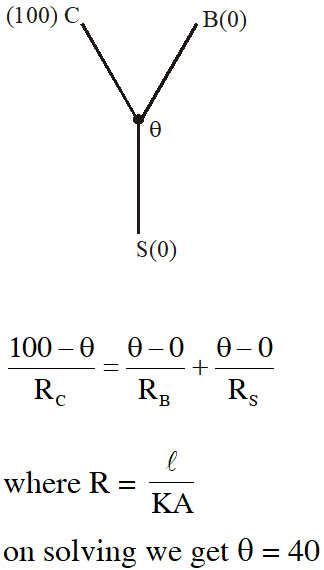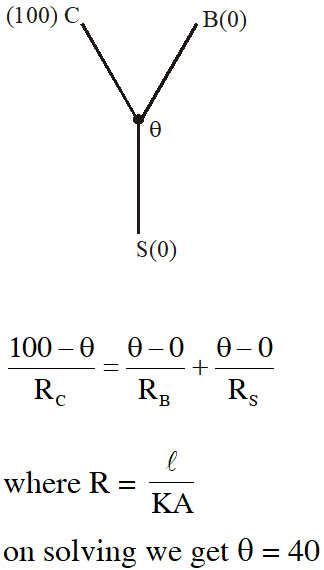Heat flow per unit time through copper rod
$=\frac{(100-40)}{\ell_{\mathrm{c}}}\left(\mathrm{K}_{\mathrm{c}} \mathrm{A}_{\mathrm{c}}\right)$
$=\frac{60}{46} \times 0.92 \times 4$
$=4.8 \mathrm{cal} / \mathrm{s}$
Heat flow per unit time through copper rod
$=\frac{(100-40)}{\ell_{\mathrm{c}}}\left(\mathrm{K}_{\mathrm{c}} \mathrm{A}_{\mathrm{c}}\right)$
$=\frac{60}{46} \times 0.92 \times 4$
$=4.8 \mathrm{cal} / \mathrm{s}$
Comments
SA
Aug. 8, 2020, 6:59 p.m.
helpfuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuu uuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLL..............................
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.