JEE Main Previous Year Question of Math with Solutions are available at eSaral. Practicing JEE Main Previous Year Papers Questions of mathematics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Q. The equation of the hyperbola whose foci are (–2,0) and (2, 0) and eccentricity is 2 is given by :
(1) $-3 x^{2}+y^{2}=3$
(2) $x^{2}-3 y^{2}=3$
(3) $3 x^{2}-y^{2}=3$
(4) $-x^{2}+3 y^{2}=3$
[AIEEE-2011]
Ans. (3)
$2 \mathrm{ae}=4$
$\mathrm{ae}=2$
$\mathrm{a}(2)=2$
$\mathrm{a}=1$
$\mathrm{b}^{2}=\mathrm{a}^{2}\left(\mathrm{e}^{2}-1\right)$
$\begin{aligned}=& 1(4-1)=3 \\ \text { equation } & \frac{\mathrm{x}^{2}}{1}-\frac{\mathrm{y}^{2}}{3}=1 \\ & 3 \mathrm{x}^{2}-\mathrm{y}^{2}=3 \end{aligned}$
Q. A tangent to the hyperbola $\frac{x^{2}}{4}-\frac{y^{2}}{2}=1$ meets $x$ -axis at $P$ and $y$ -axis at Q. Lines PR and QR are drawn such that OPRQ is a rectangle (where O is the origin). Then R lies on :
(1) $\frac{2}{x^{2}}-\frac{4}{y^{2}}=1$
(2) $\frac{4}{x^{2}}-\frac{2}{y^{2}}=1$
(3) $\frac{4}{x^{2}}+\frac{2}{y^{2}}=1$
(4) $\frac{2}{x^{2}}+\frac{4}{y^{2}}=1$
[JEE-Main (On line)-2013]
Ans. (2)
Tangent is $\frac{x}{2} \sec \theta-\frac{y}{\sqrt{2}} \tan \theta=1$
$P\left(\frac{2}{\sec \theta}, 0\right), Q\left(0,-\frac{\sqrt{2}}{\tan \theta}\right)$
$R\left(\frac{2}{\sec \theta},-\frac{\sqrt{2}}{\tan \theta}\right)=(h, k)$
Locus of $R \Rightarrow \quad \frac{4}{h^{2}}-\frac{9}{k^{2}}=1=\frac{4}{x^{2}}-\frac{9}{y^{2}}=1$
Q. A common tangent to the conics $x^{2}=6 y$ and $2 x^{2}-4 y^{2}=9$ is :
(1) $x+y=\frac{9}{2}$
(2) $x+y=1$
(3) $x-y=\frac{3}{2}$
(4) x – y = 1
[JEE-Main (On line)-2013]
Ans. (3)
Equation of tangent for $\frac{x^{2}}{(9 / 2)}-\frac{y^{2}}{(9 / 4)}=1$
is $y=m x \pm \sqrt{\frac{9}{2} m^{2}-\frac{9}{4}}$
and tangent to $x^{2}=6 y$ is $y=m x-\frac{3}{2} m^{2}$ ....(2)
Now equated ( 1) and ( 2)
Q. The eccentricity of the hyperbola whose length of the latus rectum is equal to 8 and the length of its conjugate axis is equal to half of the distance between its foci, is :
(1) $\sqrt{3}$
(2) $\frac{4}{3}$
(3) $\frac{4}{\sqrt{3}}$
(4) $\frac{2}{\sqrt{3}}$
[JEE-Main 2016]
Ans. (4)
Given
$\frac{2 \mathrm{b}^{2}}{\mathrm{a}}=8$
$2 \mathrm{b}=\mathrm{ae}$
we know
$\mathrm{b}^{2}=\mathrm{a}^{2}\left(\mathrm{e}^{2}-1\right)$
substitute $\frac{\mathrm{b}}{\mathrm{a}}=\frac{\mathrm{e}}{2}$ from ( 2) in ( 3)
$\Rightarrow \frac{\mathrm{e}^{2}}{4}=\mathrm{e}^{2}-1 \Rightarrow 4=3 \mathrm{e}^{2}$
$\Rightarrow \mathrm{e}=\frac{2}{\sqrt{3}}$
Q. A hyperbola passes through the point $\mathrm{P}(\sqrt{2}, \sqrt{3})$ and has foci at $(\pm 2,0) .$ Then the tangent to this hyperbola at $\mathrm{P}$ also passes through the point:
(1) $(-\sqrt{2},-\sqrt{3})$
(2) $(3 \sqrt{2}, 2 \sqrt{3})$
(3) $(2 \sqrt{2}, 3 \sqrt{3})$
(4) $(\sqrt{3}, \sqrt{2})$
[JEE-Main 2017]
Ans. (3)
Equation of hyperbola is $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$
foci is $(\pm 2,0)$ hence ae $=2, \Rightarrow a^{2} e^{2}=4$
$b^{2}=a^{2}\left(e^{2}-1\right)$
$\therefore a^{2}+b^{2}=4$ ...(1)
Hyperbola passes through $(\sqrt{2}, \sqrt{3})$
$\therefore \frac{2}{\mathrm{a}^{2}}-\frac{3}{\mathrm{b}^{2}}=1$ ...(2)
On solving ( 1) and ( 2)
$\mathrm{a}^{2}=8(\text { is rejected })$ and $\mathrm{a}^{2}=1$ and $\mathrm{b}^{2}=3$
$\therefore \frac{\mathrm{x}^{2}}{1}-\frac{\mathrm{y}^{2}}{3}=1$
Equation of tangent is $\frac{\sqrt{2} \mathrm{x}}{1}-\frac{\sqrt{3} \mathrm{y}}{3}=1$
Hence $(2 \sqrt{2}, 3 \sqrt{3})$ satisfy it.
Q. Tangents are drawn to the hyperbola $4 \mathrm{x}^{2}-\mathrm{y}^{2}=36$ at the point $\mathrm{P}$ and $\mathrm{Q}$. If these tangents intersect at the point $\mathrm{T}(0,3)$ then the area (in sq. units) of $\Delta \mathrm{PTQ}$ is –
(1) $54 \sqrt{3}$
(2) $60 \sqrt{3}$
(3) $36 \sqrt{5}$
(4) $45 \sqrt{5}$
[JEE-Main 2018]
Ans. (4)
Equation PQ : chord of contact T = 0
y = – 12
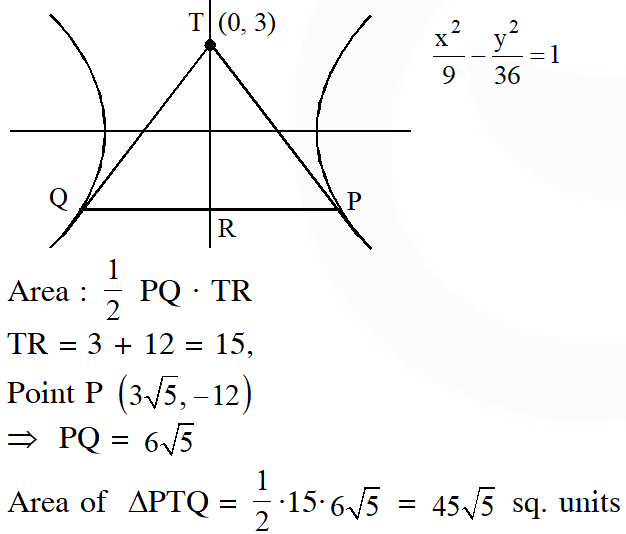
Comments
future iitian
Aug. 31, 2021, 7:41 p.m.
solutions are not at all clear please try to give clear solutions
To turn
Oct. 30, 2020, 7:56 p.m.
Emmett dddddddddd Jenna am keen is add we nnaa all manner nee d see we let me lengthens meet meeru key kk lily
To GM
