Kinematics 1D- JEE Advanced Previous Year Questions with Solutions
JEE Mains & Advanced
JEE Advanced Previous Year Questions of Physics with Solutions are available at eSaral. Practicing JEE Advanced Previous Year Papers Questions of Physics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas. Get detailed Class 11th & 12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc. eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects. Click Here for JEE main Previous Year Topic Wise Questions of Physics with Solutions Download eSaral app for free study material and video tutorials. Simulator Previous Years JEE Advanced Questions
Q. A train is moving along a straight line with a constant acceleration ‘a’. A boy standing in the train throws a ball forward with a speed of 10 m/s, at an angle of $60^{\circ}$ to the horizontal. The boy has to move forward by 1.15 m inside the train to catch the ball back at the initial height. The acceleration of the train, in $\mathrm{m} / \mathrm{s}^{2}$, is [IIT-JEE 2011]
Ans. 5 
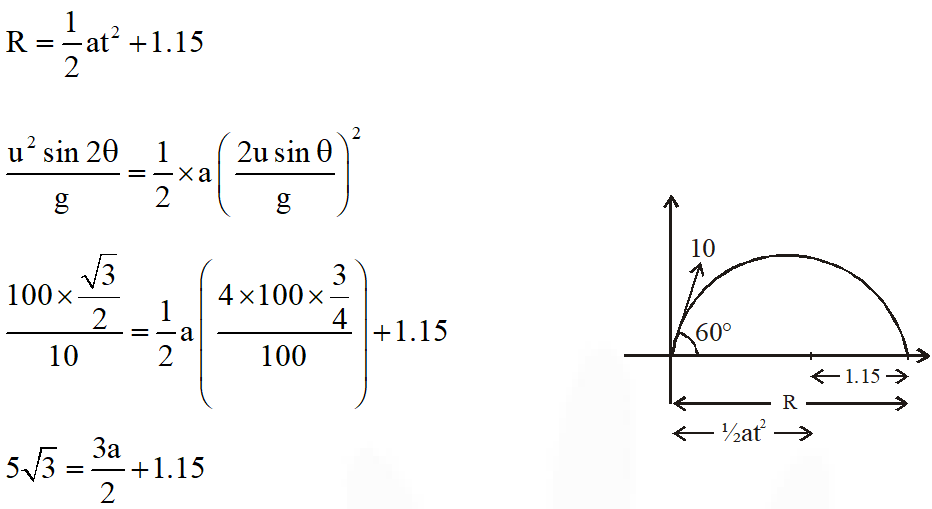
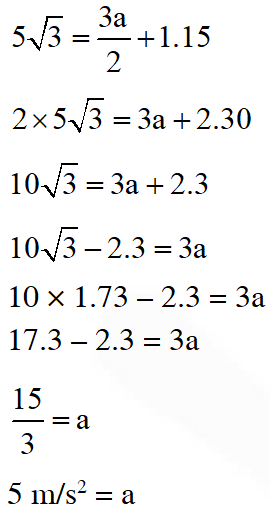
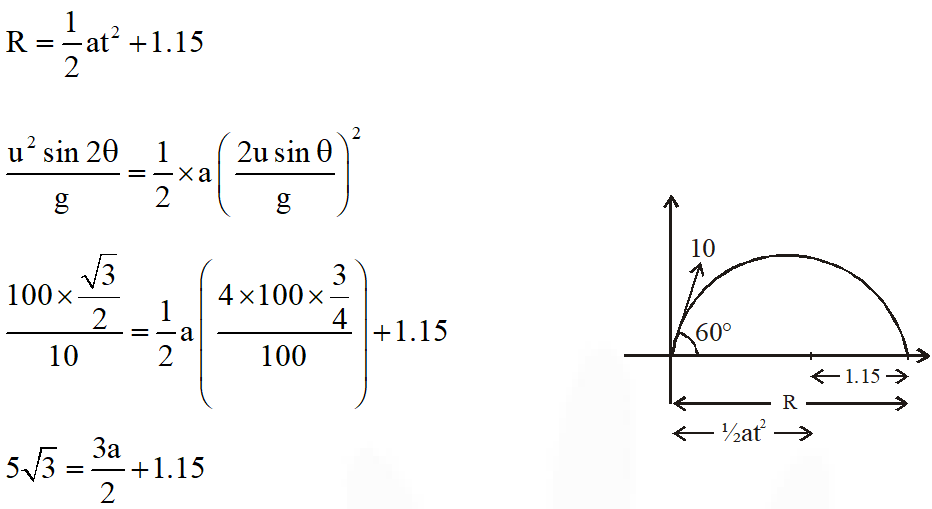
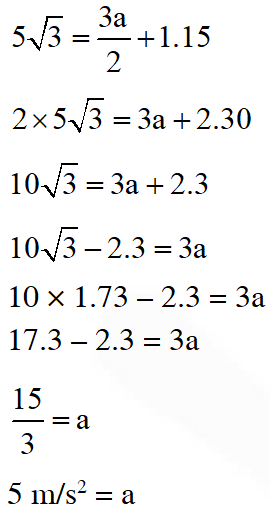
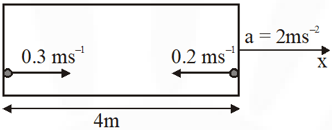
Q. A rocket is moving in a gravity free space with a constant acceleration of 2 $\mathrm{ms}^{-2}$ along + x direction (see figure). The length of a chamber inside the rocket is 4m. A ball is thrown from the left end of the chamber in + x direction with a speed of 0.3 $\mathrm{ms}^{-1}$ relative to the rocket. At the same time, another ball is thrown in –x direction with a speed of 0.2 $\mathrm{ms}^{-1}$ from its right end relative to the rocket. The time in seconds when the two balls hit each other is 
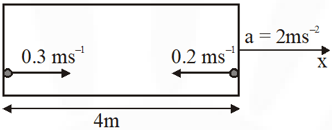[JEE Advanced 2014]
[JEE Advanced 2014] Ans. 8 or 2 Assuming open chamber 
$\mathrm{V}_{\text {relative }}=0.5 \mathrm{m} / \mathrm{s}$ $\mathrm{S}_{\text {relative }}=4 \mathrm{m}$ time $=\frac{4}{0.5}=8 \mathrm{m} / \mathrm{s}$ Alternate Assuming closed chamber In the frame of chamber : 
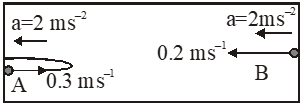Maximum displacement of ball A from its left end is $\frac{\mathrm{u}_{\mathrm{A}}^{2}}{2 \mathrm{a}}=\frac{(0.3)^{2}}{2(2)}=0.0225 \mathrm{m}$ This is negligible with respect to the length of chamber i.e. 4m. So, the collision will be verym close to the left end. Hence, time taken by ball B to reach left end will be given by $\mathrm{S}=\mathrm{u}_{\mathrm{B}} \mathrm{t}+\frac{1}{2} \mathrm{at}^{2}$ $4=(0.2)(\mathrm{t})+\frac{1}{2}(2)(\mathrm{t})^{2}$ Solving this, we get $\mathrm{t} \approx 2 \mathrm{s}$
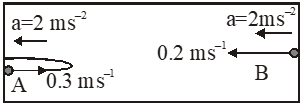$\mathrm{V}_{\text {relative }}=0.5 \mathrm{m} / \mathrm{s}$ $\mathrm{S}_{\text {relative }}=4 \mathrm{m}$ time $=\frac{4}{0.5}=8 \mathrm{m} / \mathrm{s}$ Alternate Assuming closed chamber In the frame of chamber : Maximum displacement of ball A from its left end is $\frac{\mathrm{u}_{\mathrm{A}}^{2}}{2 \mathrm{a}}=\frac{(0.3)^{2}}{2(2)}=0.0225 \mathrm{m}$ This is negligible with respect to the length of chamber i.e. 4m. So, the collision will be verym close to the left end. Hence, time taken by ball B to reach left end will be given by $\mathrm{S}=\mathrm{u}_{\mathrm{B}} \mathrm{t}+\frac{1}{2} \mathrm{at}^{2}$ $4=(0.2)(\mathrm{t})+\frac{1}{2}(2)(\mathrm{t})^{2}$ Solving this, we get $\mathrm{t} \approx 2 \mathrm{s}$ Q. Airplanes A and B are flying with constant velocity in the same vertical plane at angles $30^{\circ}$ and $60^{\circ}$ with respect to the horizontal respectively as shown in figure. The speed of A is $\mathrm{ms}^{-1}$. At time t = 0 s, an observer in A finds B at a distance of 500 m. This observer sees B moving with a constant velocity perpendicular to the line of motion of A. If at t = $\mathrm{t}_{0}$, A just escapes being hit by B, $\mathrm{t}_{0}$ in seconds is 
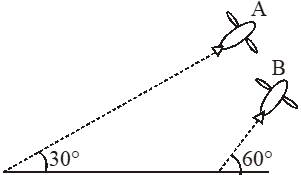[JEE Advanced-2014]
[JEE Advanced-2014] Ans. 5 
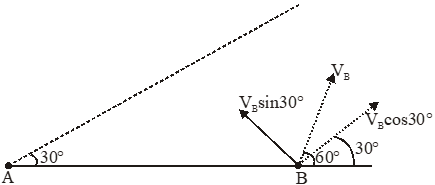As observed from A, B moves perpendicular to line of motion of A. It means velocity of B along A is equal to velocity of A $\mathrm{V}_{\mathrm{B}} \cos 30=100 \sqrt{3}$ $\mathrm{V}_{\mathrm{B}}=200$ If A is observer A remains stationary therefore $\mathrm{t}=\frac{500}{\mathrm{V}_{\mathrm{B}} \sin 30}=\frac{500}{100}=5$
As observed from A, B moves perpendicular to line of motion of A. It means velocity of B along A is equal to velocity of A $\mathrm{V}_{\mathrm{B}} \cos 30=100 \sqrt{3}$ $\mathrm{V}_{\mathrm{B}}=200$ If A is observer A remains stationary therefore $\mathrm{t}=\frac{500}{\mathrm{V}_{\mathrm{B}} \sin 30}=\frac{500}{100}=5$ Q. Consider an expanding sphere of instantaneous radius R whose total mass remains constant. The expansion is that the instantaneous density $\rho$ remains uniform throughout the volume. the rate of fractional change in density is $\left(\frac{1}{\rho} \frac{d \rho}{d t}\right)$ constant. the velocity v of any point on the surface of the expanding sphere is proportional to (A) $R^{3}$ (B) $\frac{1}{R}$ (C) $\mathrm{R}$ (D) $R^{2 / 3}$ [JEE Advanced-2017]
Ans. (C)
Comments
Anshuman pandey
July 17, 2023, 6:35 a.m.
mai to class 9 me hu mai ye solve kar pa rha hu kya ye bat achi hai ya overconfidence wali bat hai?
Akash
March 29, 2022, 8:11 p.m.
Great
Try to help poor students by providing subscription at low cost🤗🤗🤗🤗
Ashish chanchlani
Dec. 22, 2020, 2:26 p.m.
My memories I use to solve these questions. Physics was my favourite subject.