Kinematics 2D - JEE Main Previous Year Questions with Solutions

JEE Main Previous Year Question of Physics with Solutions are available here. Practicing JEE Main Previous Year Papers Questions of Physics will help all the JEE aspirants in realizing the question pattern as well as help in analyzing their weak & strong areas. Get detailed Class 11th &12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc. eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects. Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more. Download eSaral app for free study material and video tutorials. Simulator   Previous Years JEE Advanced Questions

Q. A train is moving along a straight line with a constant acceleration ‘a’. A boy standing in the train throws a ball forward with a speed of 10 m/s, at an angle of $60^{\circ}$ to the horizontal. The boy has to move forward by 1.15 m inside the train to catch the ball back at the initial height. The acceleration of the train, in $\mathrm{m} / \mathrm{s}^{2}$, is - [IIT-JEE 2011]

Ans. 5

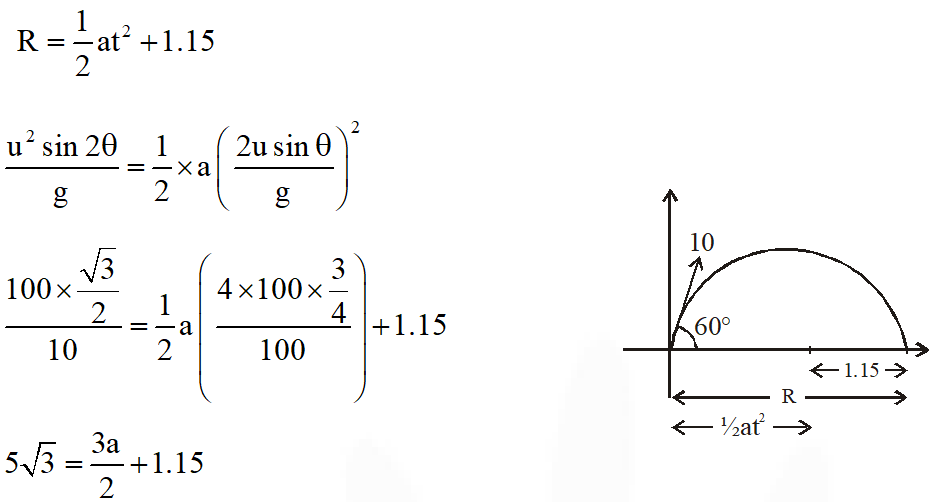
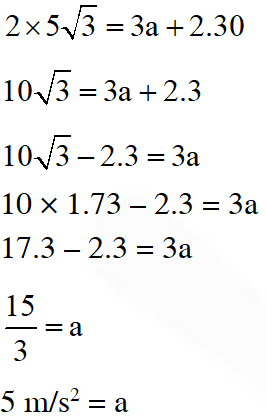
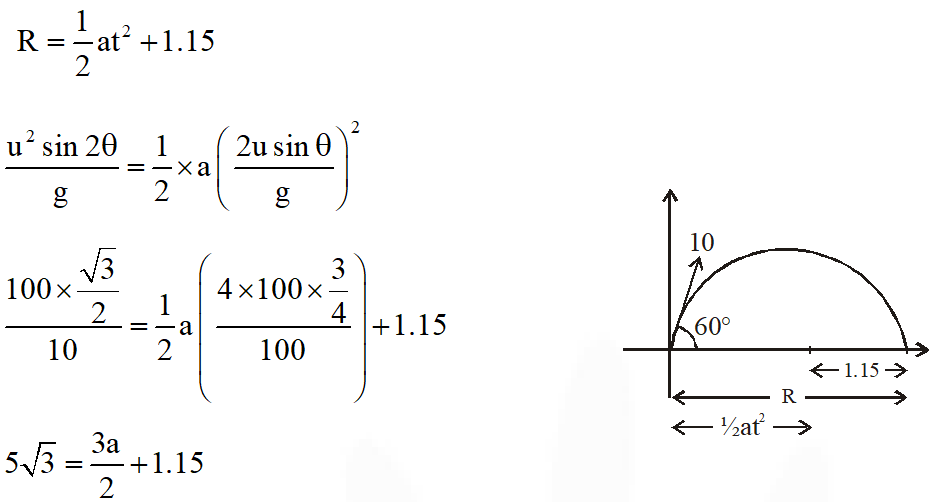
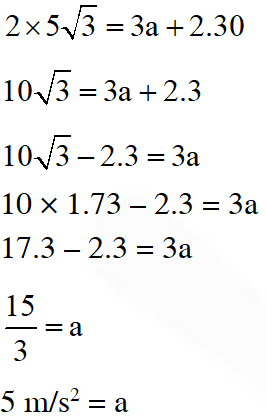
Q. A rocket is moving in a gravity free space with a constant acceleration of 2 $\mathrm{ms}^{-2}$along + x direction (see figure). The length of a chamber inside the rocket is 4m. A ball is thrown from the left end of the chamber in + x direction with a speed of 0.3 $\mathrm{ms}^{-1}$ relative to the rocket. At the same time, another ball is thrown in –x direction with a speed of 0.2 $\mathrm{ms}^{-1}$ from its right end relative to the rocket. The time in seconds when the two balls hit each other is - [JEE Advanced 2014]

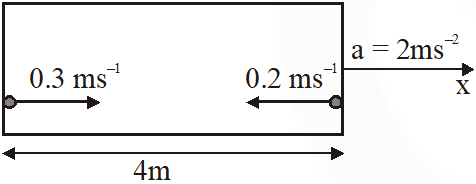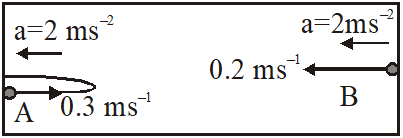Ans. 8 or 2 Assuming open chamber $\mathrm{V}_{\text {relative }}=0.5 \mathrm{m} / \mathrm{s}$ $S_{\text {relative }}=4 \mathrm{m}$ time $=\frac{4}{0.5}=8 \mathrm{s}$ Alternate Assuming closed chamber In the frame of chamber : Maximum displacement of ball A from its left end is $\frac{\mathrm{u}_{\mathrm{A}}^{2}}{2 \mathrm{a}}=\frac{(0.3)^{2}}{2(2)}=0.0225 \mathrm{m}$ This is negligible with respect to the length of chamber i.e. 4m. So, the collision will be very close to the left end. Hence, time taken by ball B to reach left end will be given by $\mathrm{S}=\mathrm{u}_{\mathrm{B}} \mathrm{t}+\frac{1}{2} \mathrm{at}^{2}$ $4=(0.2)(t)+\frac{1}{2}(2)(t)^{2}$ Solving this, we get $\mathrm{t} \approx 2 \mathrm{s}$

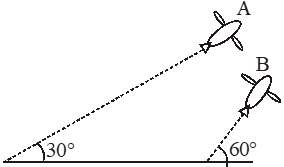
Q. Airplanes A and B are flying with constant velocity in the same vertical plane at angles $30^{\circ}$ and $60^{\circ}$ with respect to the horizontal respectively as shown in figure. The speed of A is $\mathrm{ms}^{-1}$. At time t = 0 s, an observer in A finds B at a distance of 500 m. This observer sees B moving with a constant velocity perpendicular to the line of motion of A. If at t = $t_{0}$, A just escapes being hit by B, $t_{0}$ in seconds is [JEE Advanced 2014]

Ans. 5 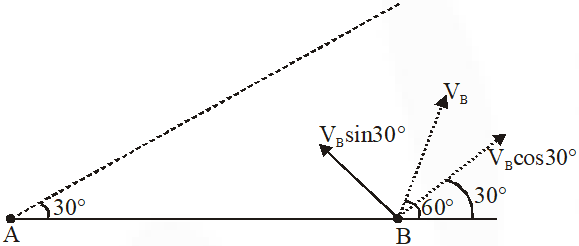As observed from A, B moves perpendicular to line of motion of A. It means velocity of B along A is equal to velocity of A $\mathrm{V}_{\mathrm{B}} \cos 30=100 \sqrt{3}$ $\mathrm{V}_{\mathrm{B}}=200$ If A is observer A remains stationary therefore $\mathrm{t}=\frac{500}{\mathrm{V}_{\mathrm{B}} \sin 30}=\frac{500}{100}=5$

Q. A ball is projected from the ground at an angle of $45^{\circ}$ with the horizontal surface. It reaches a maximum height of 120 m and returns to the ground. Upon hitting the ground for the first time, it loses half of its kinetic energy. Immediately after the bounce, the velocity of the ball makes an angle of $30^{\circ}$ with the horizontal surface. The maximum height it reaches after the bounce, in metres, is [JEE Advanced 2018]

Ans. 30 $\mathrm{H}_{1}=\frac{\mathrm{u}^{2} \sin ^{2} 45}{2 \mathrm{g}}=120$ $\Rightarrow \frac{\mathrm{u}^{2}}{4 \mathrm{g}}=120$ ....(i) when half of kinetic energy is lost $\mathrm{v}=\frac{\mathrm{u}}{\sqrt{2}}$ $\mathrm{H}_{2}=\frac{\left(\frac{\mathrm{u}}{\sqrt{2}}\right)^{2} \sin ^{2} 30}{2 \mathrm{g}}=\frac{\mathrm{u}^{2}}{16 \mathrm{g}}$ from (i) & (ii) $\mathrm{H}_{2}=\frac{\mathrm{H}_{1}}{4}=30 \mathrm{m}$ on 30.00

To plan revision across Kinematics (2D) and related topics, explore the JEE Mains chapter wise PYQ collection for organised chapter-wise practice.

If full mock-exam conditions suit you better than isolated Kinematics (2D) questions, our JEE Main last year paper is the natural next step.