JEE Main Previous Year Question of Physics with Solutions are available here. Practicing JEE Main Previous Year Papers Questions of Physics will help all the JEE aspirants in realizing the question pattern as well as help in analyzing their weak & strong areas.
Get detailed Class 11th &12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Simulator
Previous Years AIEEE/JEE Mains Questions
Q. One kg of a diatomic gas is at a pressure of $8 \times 10^{4} \mathrm{N} / \mathrm{m}^{2}$. The density of the gas is $4 \mathrm{kg} / \mathrm{m}^{3}$. What is the energy of the gas due to its thermal motion ?
(1) $6 \times 10^{4} \mathrm{J}$
(2) $7 \times 10^{4} \mathrm{J}$
(3) $3 \times 10^{4} \mathrm{J}$
(4) $5 \times 10^{4} \mathrm{J}$
Directions : Question number 11, 12 and 13 are based on the following paragraph.
Two moles of helium gas are taken over the cycle ABCDA, as shown in the P–T diagram.
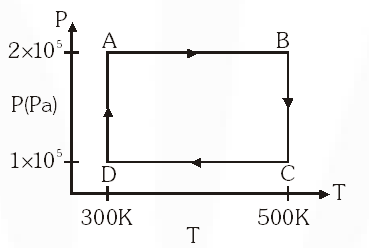 [AIEEE-2009]
[AIEEE-2009]
 [AIEEE-2009]
[AIEEE-2009]
Ans. (3 )
$\frac{P M}{R T}=\rho$
$\frac{P}{\rho}=\frac{R T}{M}$
$\mathbf{U}=\frac{3}{2} n R T=\frac{3}{2} m\left(\frac{R T}{M}\right)$
Q. A thermally insulated vessel contains an ideal gas of molecular mass M and ratio of specific heats $\gamma$. It is moving with speed v and is suddenly broght to rest. Assuming no heat is lost to the surroundings, its temperature increases by :-
(1) $\frac{\gamma \mathrm{Mv}^{2}}{2 \mathrm{R}}$
(2) $\frac{(\gamma-1)}{2 \mathrm{R}} \mathrm{Mv}^{2}$
(3) $\frac{(\gamma-1)}{2(\gamma+1) \mathrm{R}} \mathrm{Mv}^{2}$
(4) $\frac{(\gamma-1)}{2 \gamma \mathrm{R}} \mathrm{Mv}^{2}$
[AIEEE-2011]
Ans. (2)
$\frac{1}{2} m v^{2}=\frac{n R \Delta T}{\gamma-1}$
$\Delta \mathrm{T}=\frac{1}{2} \frac{m}{n} \frac{(\gamma-1) v^{2}}{R}$
Q. Three perfect gases at absolute temperatures $\mathrm{T}_{1}, \mathrm{T}_{2}$ and $\mathrm{T}_{3}$ are mixed. The masses of molecules are m1, m2, and m3 and the number of molecules are $\mathrm{n}_{1}, \mathrm{n}_{2}$ and $\mathrm{n}_{3}$ respectively. Assuming no loss of energy, then final temperature of the mixture is :-
(1) $\frac{n_{1} \mathrm{T}_{1}^{2}+\mathrm{n}_{2} \mathrm{T}_{2}^{2}+\mathrm{n}_{3} \mathrm{T}_{3}^{2}}{\mathrm{n}_{1} \mathrm{T}_{1}+\mathrm{n}_{2} \mathrm{T}_{2}+\mathrm{n}_{3} \mathrm{T}_{3}}$
(2) $\frac{n_{1}^{2} T_{1}^{2}+n_{2}^{2} T_{2}^{2}+n_{3}^{2} T_{3}^{2}}{n_{1} T_{1}+n_{2} T_{2}+n_{3} T_{3}}$
(3) $\frac{\mathrm{T}_{1}+\mathrm{T}_{2}+\mathrm{T}_{3}}{3}$
(4) $\frac{\mathrm{n}_{1} \mathrm{T}_{1}+\mathrm{n}_{2} \mathrm{T}_{2}+\mathrm{n}_{3} \mathrm{T}_{3}}{\mathrm{n}_{1}+\mathrm{n}_{2}+\mathrm{n}_{3}}$
[AIEEE-2011]
Ans. (4)
$\mathrm{n}_{1} \mathrm{C}_{\mathrm{V}} \mathrm{T}_{1}+\mathrm{n}_{2} \mathrm{C}_{\mathrm{V}} \mathrm{T}_{2}+\mathrm{n}_{3} \mathrm{C}_{\mathrm{V}} \mathrm{T}_{3}=\left(\mathrm{n}_{1}+\mathrm{n}_{2}+\mathrm{n}_{3}\right) \mathrm{C}_{\mathrm{v}} \mathrm{T}$
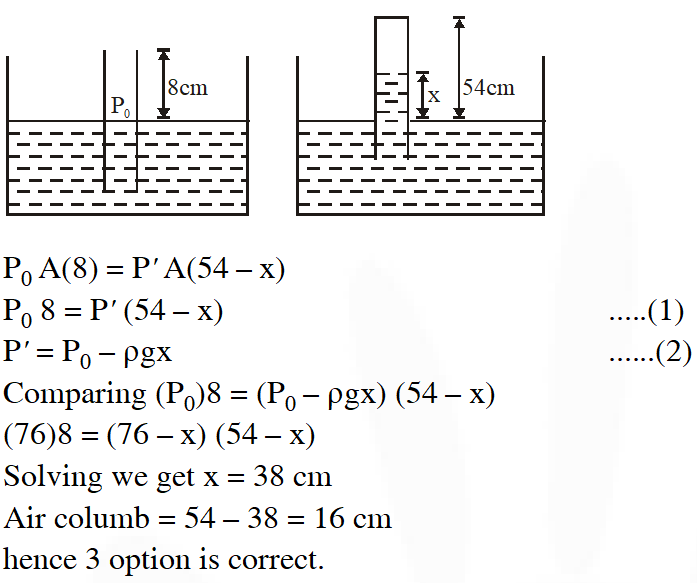
Q. An open glass tube is immersed in mercury in such a way that a length of 8 cm extends above the mercury level. The open of the tube is then closed and sealed and the tube is raised vertically up by addition 46 cm. What will be length of the air column above mercury in the tube now ?
(Atmospheric pressure = 76 cm of Hg)
(1) 38 cm (2) 6 cm (3) 16 cm (4) 22 cm
[jEE-Mains-2014]
Ans. (3)

Q. Consider an ideal gas confined in an isolated closed chamber. As the gas undergoes an adiabatic expansion, the average time of collision between molecules increases as $\mathbf{V} \mathbf{q}$, where V is the volume of the gas. The value of q is :- $\left(\gamma=\frac{\mathrm{C}_{\mathrm{p}}}{\mathrm{C}_{\mathrm{v}}}\right)$
(1) $\frac{\gamma+1}{2}$
( 2)$\frac{\gamma-1}{2}$
(3) $\frac{3 y+5}{6}$
(4) $\frac{3 \gamma-5}{6}$
[jEE-Mains-2015]
Ans. (1)
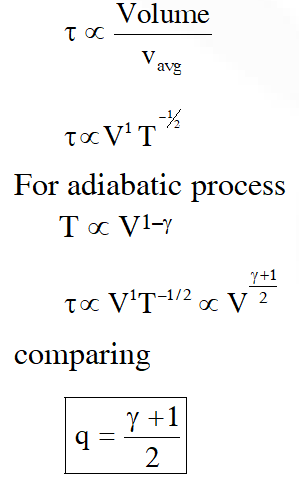
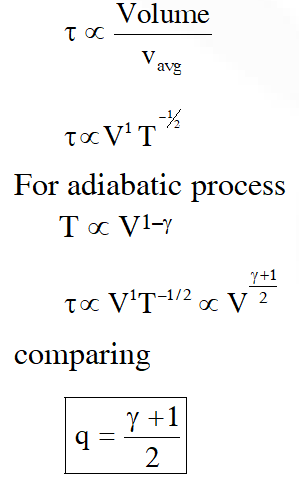
Q. The temperature of an open room of volume $30 \mathrm{m}^{3}$ increases from $17^{\circ} \mathrm{C}$ to $27^{\circ} \mathrm{C}$ due to sunshine. The atmospheric pressure in the room remains $1 \times 10^{5} \mathrm{Pa} .$ If $\mathrm{n}_{1}$ and $\mathrm{n}_{\mathrm{f}}$ are the number of molecules in the room before and after heating, then $\mathrm{n}_{\mathrm{f}}-\mathrm{n}_{\mathrm{i}}$will be :-
(1) $2.5 \times 10^{25}$
(2) $-2.5 \times 10^{25}$
(3) $-1.61 \times 10^{23}$
(4) $1.38 \times 10^{23}$
[jEE-Mains-2017]
Ans. (2)
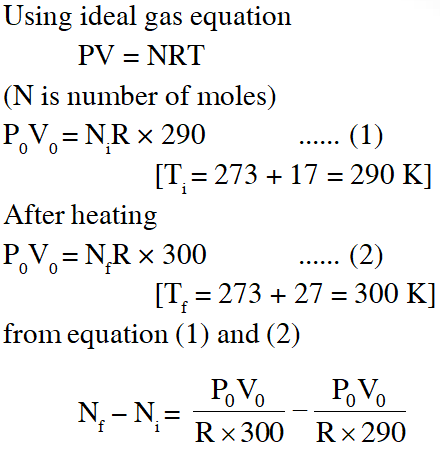
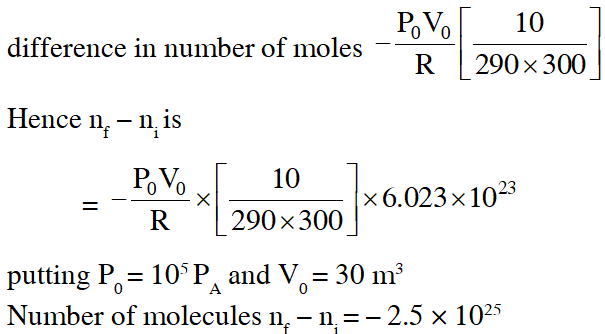
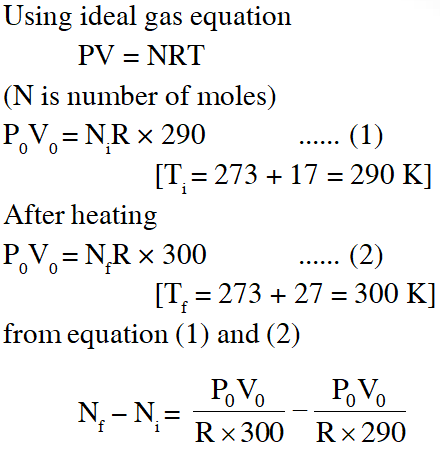
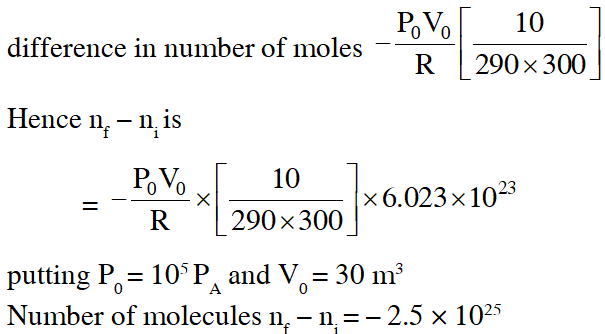
Q. The mass of a hydrogen molecule is $3.32 \times 10^{-27} \mathrm{kg} .$ If $102^{23}$ hydrogen molecules strike, per second, a fixed wall of area 2 cm2 at an angle of $45^{\circ}$ to the normal, and rebound elastically with a speed of $10^{3}$ m/s, then the pressure on the wall is nearly :
(1) $4.70 \times 10^{3} \mathrm{N} / \mathrm{m}^{2}$
(2) $2.35 \times 10^{2} \mathrm{N} / \mathrm{m}^{2}$
(3) $4.70 \times 10^{2} \mathrm{N} / \mathrm{m}^{2}$
(4) $2.35 \times 10^{3} \mathrm{N} / \mathrm{m}^{2}$
[jEE-Mains-2018]
Ans. (4)
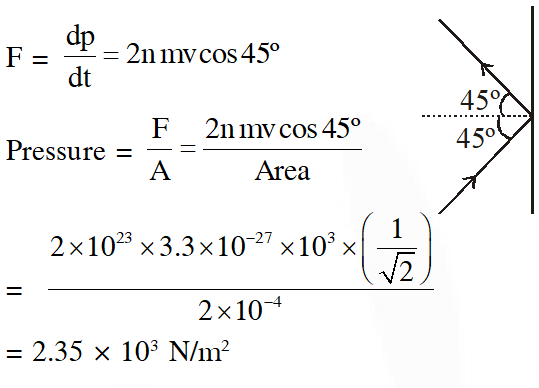
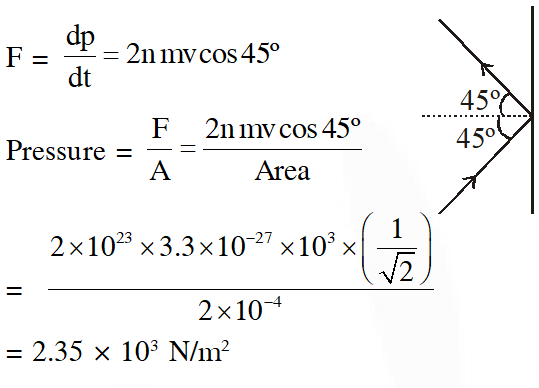
Comments
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
