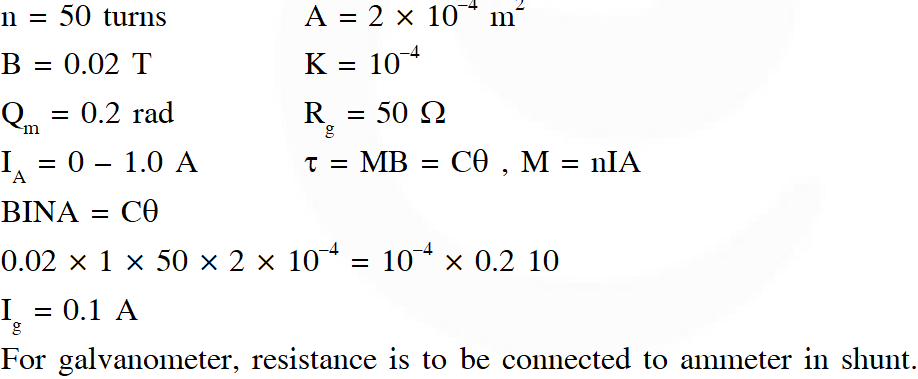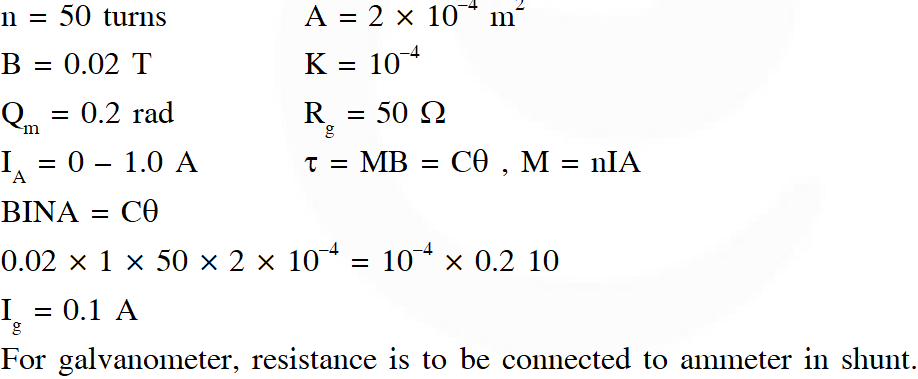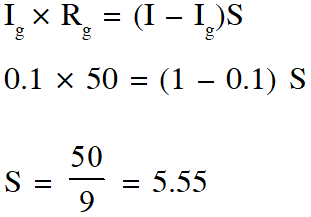JEE Advanced Previous Year Questions of Physics with Solutions are available at eSaral. Practicing JEE Advanced Previous Year Papers Questions of Physics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
Get detailed Class 11th & 12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Click Here for JEE main Previous Year Topic Wise Questions of Physics with Solutions
Download eSaral app for free study material and video tutorials.
Simulator
Previous Years JEE Advanced Questions
Comprehension Type
Electrical resistance of certain materials, known as superconductors, changes abruptly from a nonzero value to zero as their temperature is lowered below a critical temperature $\mathrm{T}_{\mathrm{C}}$ (0). An interesting property of superconductors is that their critical temperature becomes smaller than $\mathrm{T}_{\mathrm{C}}$ (0) if they are placed in a magnetic field, i.e., the critical temperature $\mathrm{T}_{\mathrm{C}}$ (B) is a function of the magnetic field strength B. The dependence of $\mathrm{T}_{\mathrm{C}}$ (B) on B is shown in the figure.
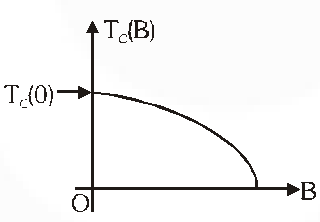Paragraph for Questions 15 & 16
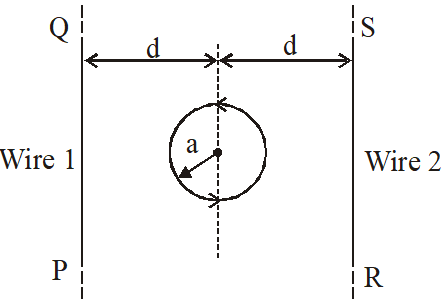
The figure shows a circular loop of radius a with two long parallel wires (numbered 1 and 2) all in the plane of the paper. The distance of each wire from the centre of the loop is d. The loop and the wires are carrying the same current I. The current in the loop is in the counterclockwise direction if seen from above.
A charged particle (electron or proton) is introduced at the origin (x = 0, y = 0, z = 0) with a given initial velocity $\overrightarrow{\mathbf{v}}$. A uniform electric field $\overrightarrow{\mathrm{E}}$ and a uniform magnetic field $\overrightarrow{\mathrm{B}}$ exist everywhere. The velocity $\overrightarrow{\mathbf{V}}$, electric field $\overrightarrow{\mathrm{E}}$ and magnetic field $\overrightarrow{\mathrm{B}}$ are given in column 1, 2 and 3, respectively. The quantities $E_{0}, B_{0}$ are positive in magnitude.
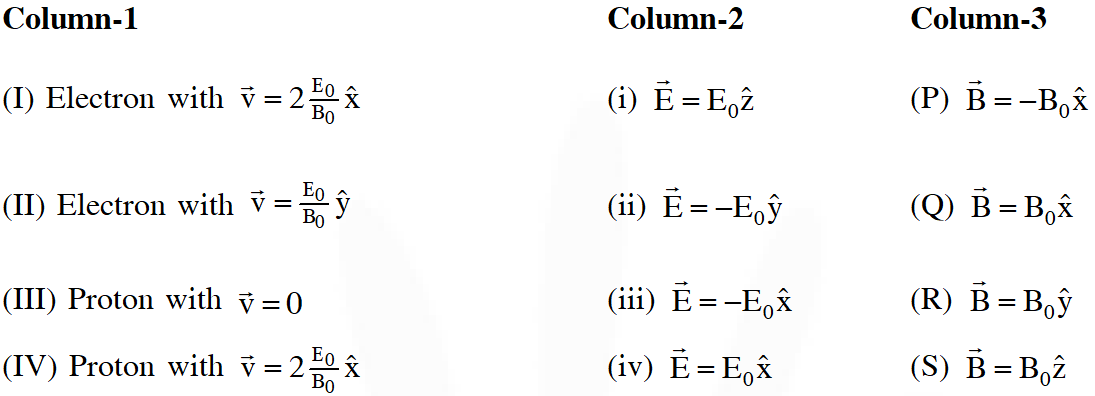
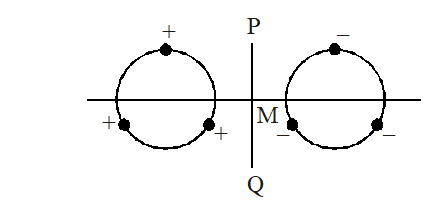
Q. Six point charges, each of the same magnitude q, are arranged in different manners as shown in Column II. In each case, a point M and a line PQ passing through M are shown. Let E be the electric field and V be the electric potential at.M (poteptial at infinity is zero) due to the given charge distribution when it is at rest. Now, the whole system is set into rotation with a constant angular velocity about the line PQ. Let B be the magnetic field at M and µ be the magnetic moment of the system in this condition. Assume each rotating charge to be equivalent to a steady current.
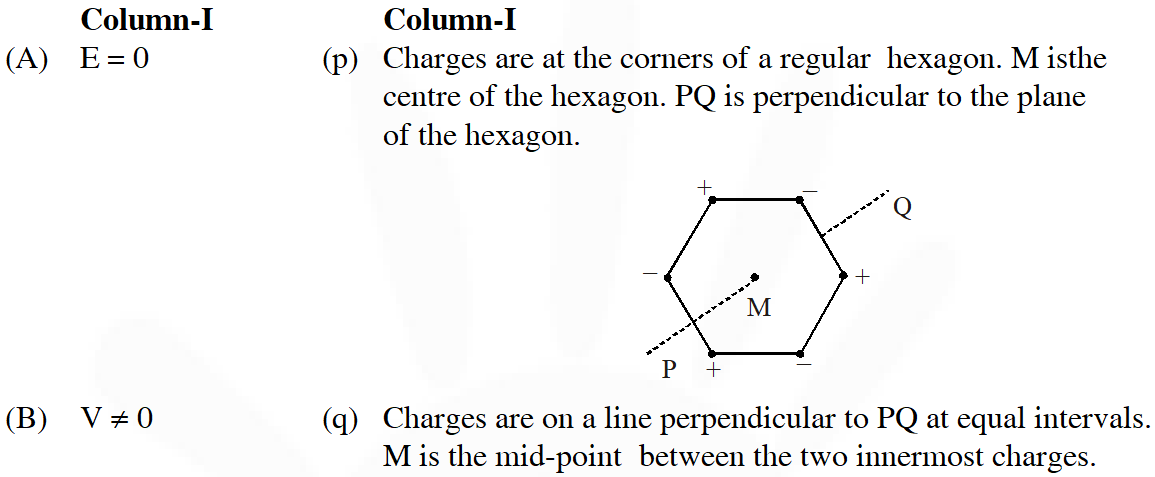
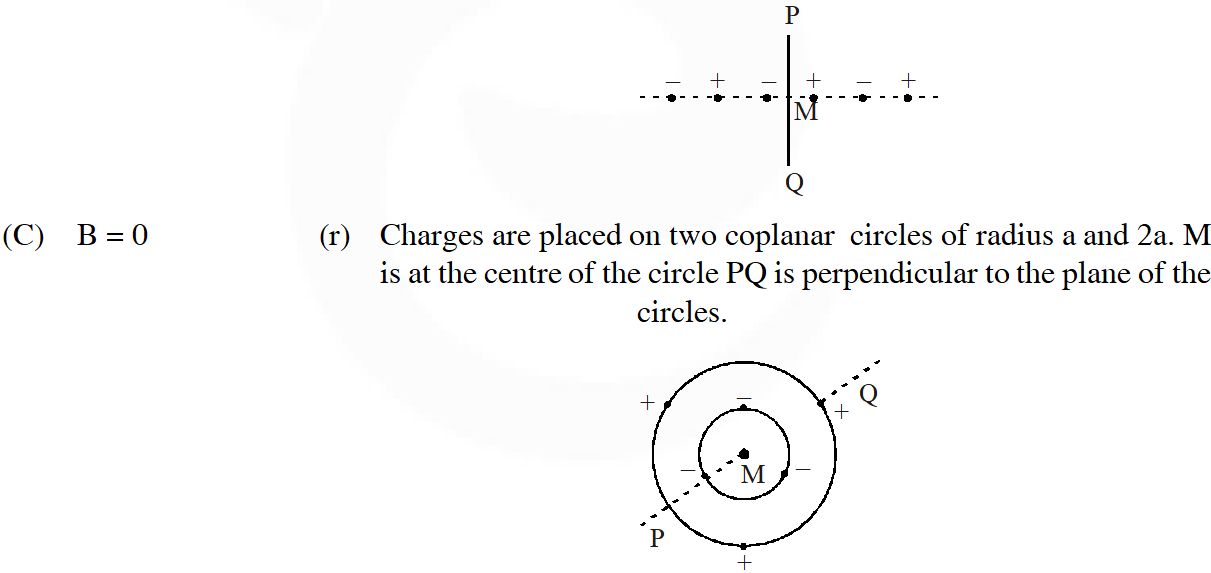
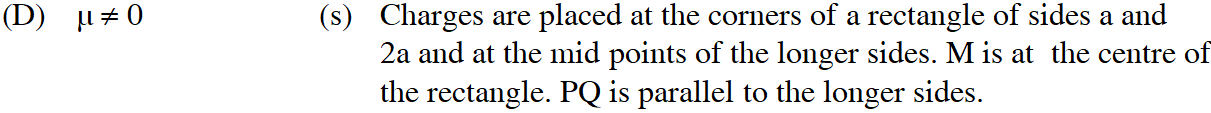
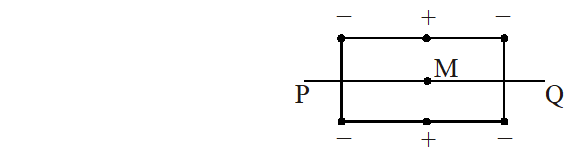(t) Charges are placed on two coplanar, identical insulating rings at equal intervals. M is the mid-point btween the centres of the rings.
PQ is perpendicular to the line joining the centres and coplanar to the rings.
[JEE-2009]
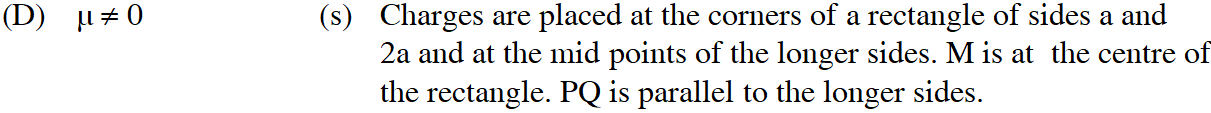
(t) Charges are placed on two coplanar, identical insulating rings at equal intervals. M is the mid-point btween the centres of the rings.
PQ is perpendicular to the line joining the centres and coplanar to the rings.
[JEE-2009]
Ans. ($(\mathrm{A}) \rightarrow \mathrm{p}, \mathrm{r}, \mathrm{s}(\mathrm{B}) \rightarrow \mathrm{r}, \mathrm{s}(\mathrm{C}) \rightarrow \mathrm{p}, \mathrm{q}, \mathrm{t}(\mathrm{D}) \rightarrow \mathrm{r}, \mathrm{s}$)
Q. Column II shows five systems in which two objects are labelled as X and Y. Also in each case a point P is shown. Column I gives some statements about X and/or Y. Match these statements to the appropriate system(s) from Column II
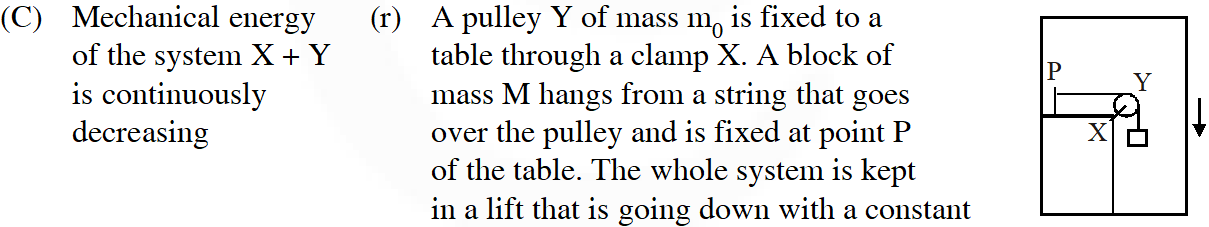
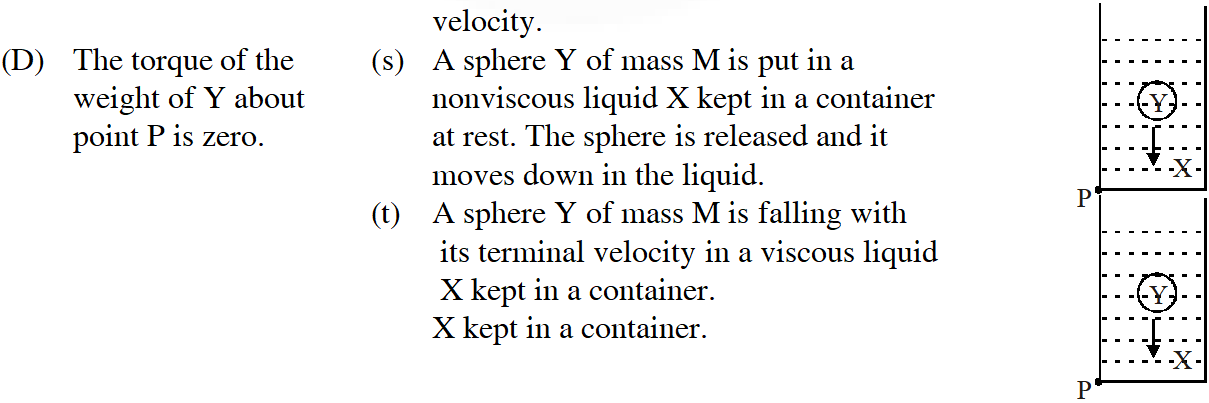[JEE-2009]
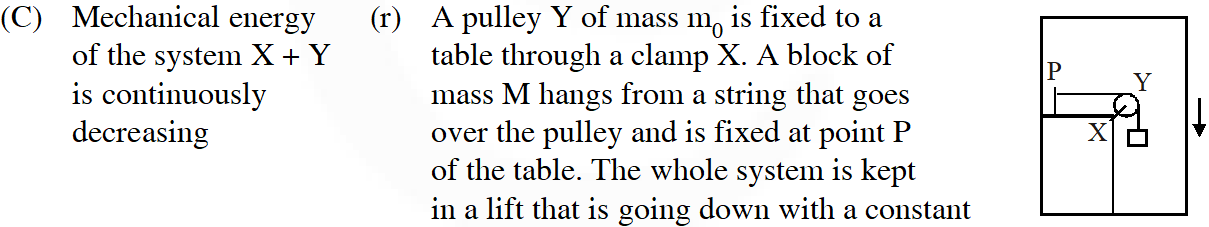
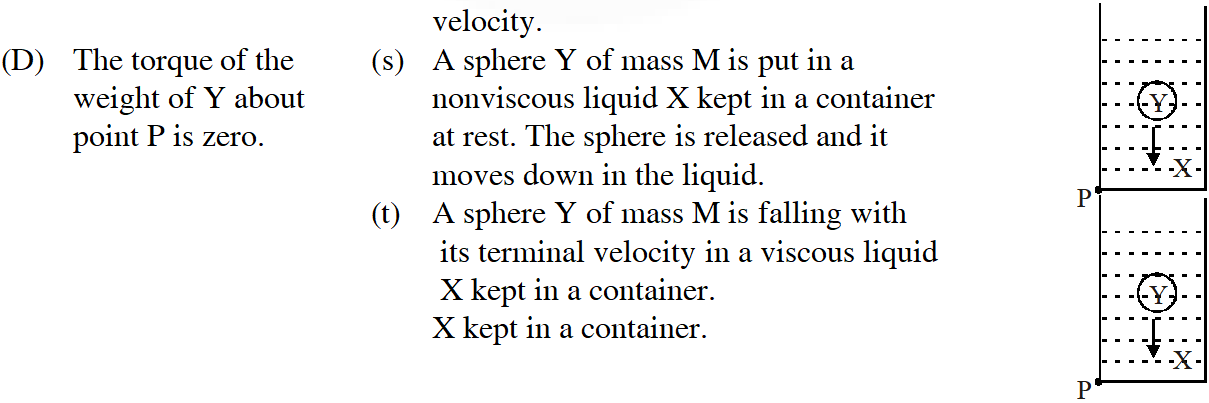[JEE-2009]
Ans. ($(A) \rightarrow p, t(B) \rightarrow q, s, t(C) \rightarrow p, r, t(D) \rightarrow q$)
(p)
(A) Total contact force = $\sqrt{\mathrm{N}^{2}+\mathrm{f}^{2}}$ = mg
(B) X is fixed therefore P.E. remain same
(C) Potential energy of 'Y' is decreasing as it slide down the plane and K.E. is not increasing
(D) Toque of weight of y is
$\tau=\operatorname{mg} \ell \cos \theta \Rightarrow \tau \neq 0$
(q)
(A) Force due to both 'X' and 'Z' on 'Y' is equal to mg
(B) As the system is moving up P.E. of system is increasing
(C) Mechanical energy of total system is increasing
(D) As the force passes through 'p' torque about p is zero
(r)
(A) Force on 'X' due to Y
$\mathrm{F}_{\mathrm{net}}=\sqrt{2} \mathrm{T} \Rightarrow \sqrt{2} \mathrm{mg}$
(B) System is moving down therefore P.E. is decreasing
(C) System is moving down with constant speed with constant speed therefore machanical energy is decreasing
(D) $\tau=\operatorname{mg} \ell \Rightarrow \tau \neq 0$
(s)
(A) Force exerted by (X) on 'Y' is less than mg and its magnitude $\mathrm{f}_{\mathrm{B}}=\mathrm{Vd}_{\mathrm{t}} \mathrm{g}$
(B) As the ball moves down it displaces the water to its higher position hence P.E. of water increases
(C) As no desssipitative force acts on it mechanical energy is conserved
(D) Torque is non-zero about p
(t) Similar to 's' but it is viscous fluid therefore total mechanical energy decreases with time.
Q. A steady current I goes through a wire loop PQR having shape of a right angle triangle with PQ = 3x, PR = 4x and QR = 5x. If the magnitude of the magnetic field at P due to this loop is $\left(\frac{\mu_{0} I}{48 \pi x}\right)$, find the value of k.
[2009, 6M]
Ans. 7
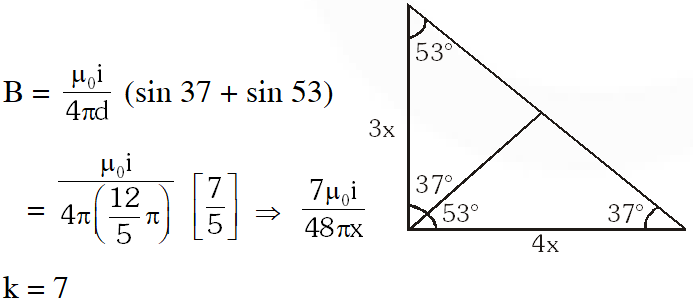
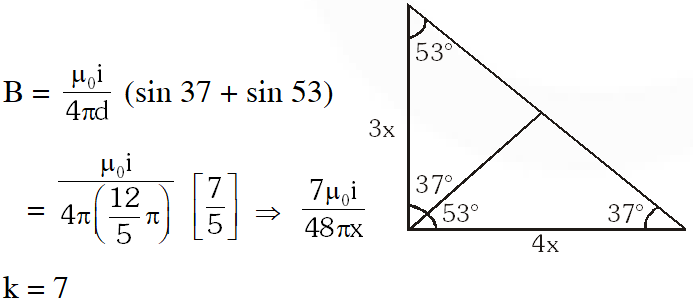
Q. A thin flexible wire of length L is connected to two adjacent fixed points and carries a current I in the clockwise direction, as shown in the figure. When the system is put in a uniform magnetic field of strength B going into the plane of the paper, the wire takes the shape of a circle. The tension in the wire is :
(A) IBL (B) $\frac{I B L}{\pi}$ (C) $\frac{I B L}{2 \pi}$ $(\mathrm{D}) \frac{I B L}{4 \pi}$
[2010, 3M]
(A) IBL (B) $\frac{I B L}{\pi}$ (C) $\frac{I B L}{2 \pi}$ $(\mathrm{D}) \frac{I B L}{4 \pi}$
[2010, 3M]
Ans. (C)
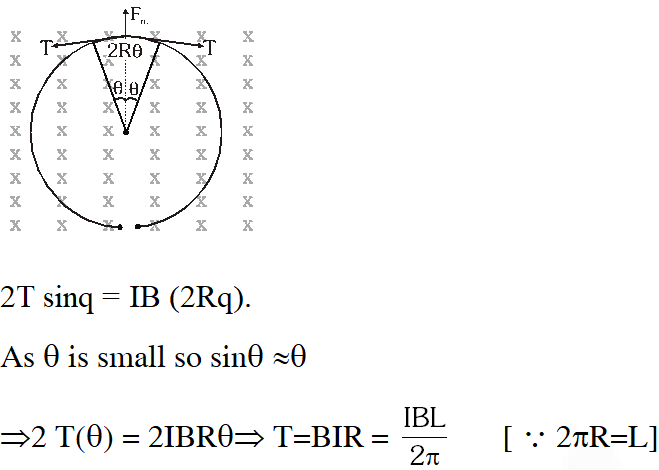
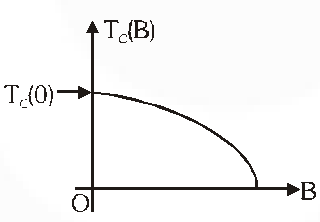
Q. In the graphs below, the resistance R of a superconductor is shown as a function of its temperature T for two different magnetic fields $\mathrm{B}_{1}$ (sold line) and $\mathrm{B}_{2}$ (dashed line). If $\mathrm{B}_{2}$ is larger than $\mathrm{B}_{1}$, which of the following graphs shows the correct variation of R with T in these fields?
[JEE2010]
[JEE2010]
Ans. (A)
If $\mathrm{B}_{2}>\mathrm{B}_{1}$, critical temperature, (at which resistance of semiconductors abrupty becomes zero) in case 2 will be less than compared to case 1.
Q. A superconductor has $\mathrm{T}_{\mathrm{C}}$ (0) = 100 K. When a magnetic field of 7.5 Tesla is applied, its $\mathrm{T}_{\mathrm{C}}$ decreases to 75 K. For this material one can definitely say that when
(A) $\mathrm{B}=5$ Tesla, $\mathrm{T}_{\mathrm{C}}(\mathrm{B})=80 \mathrm{K}$
(B) $\mathrm{B}=5$ Tesla, $75 \mathrm{K}<\mathrm{T}_{\mathrm{C}}(\mathrm{B})<100 \mathrm{K}$
(C) $\mathrm{B}=10$ Tesla, $75 \mathrm{K}<\mathrm{T}_{\mathrm{c}}(\mathrm{B})<100 \mathrm{K}$
(D) $\mathrm{B}=10$ Tesla, $\mathrm{T}_{\mathrm{c}}(\mathrm{B})=70 \mathrm{K}$
[JEE2010]
Ans. (B)
With increase in temperature, TC is decreasing.
$\mathrm{T}_{\mathrm{c}}$ (0) = 100 K
$\mathrm{T}_{\mathrm{c}}$ = 75 K at B = 7.5 T
Hence, at B = 5T, $\mathrm{T}_{\mathrm{c}}$ should line between 75 K and 100 K
Q. An electron and a proton are moving on straight parallel paths with same velocity. They enter a semi-infinite region of uniform magnetic field perpendicular to the velocity. Which of the following statement(s) is/are true?
(A) they will never come out of the magnetic field region
(B) they will come out travelling along parallel paths
(C) they will come out of the same time
(D) they will come out at different times
[IIT-JEE 2011]
Ans. (B,D)
By diagram B is true.
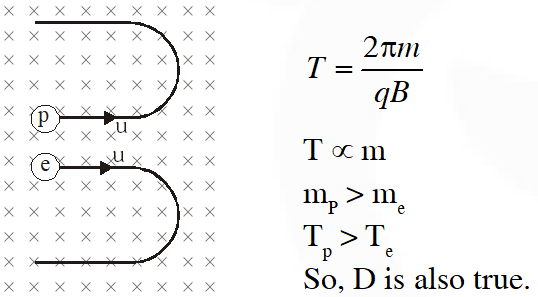
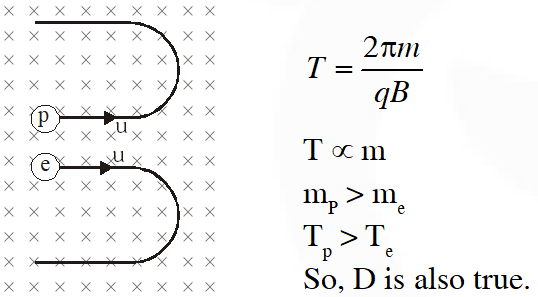
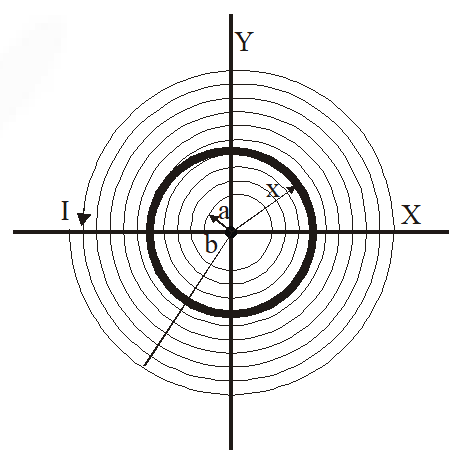
Q. A long insulated copper wire is closely wound as a spiral of ‘N’ turns. The spiral has inner radius ‘a’ and outer radius ‘b’. The spiral lies in the X-Y plane and a steady current ‘I’ flows through the wire. The Z-component of the magnetic field at the center of the spiral is
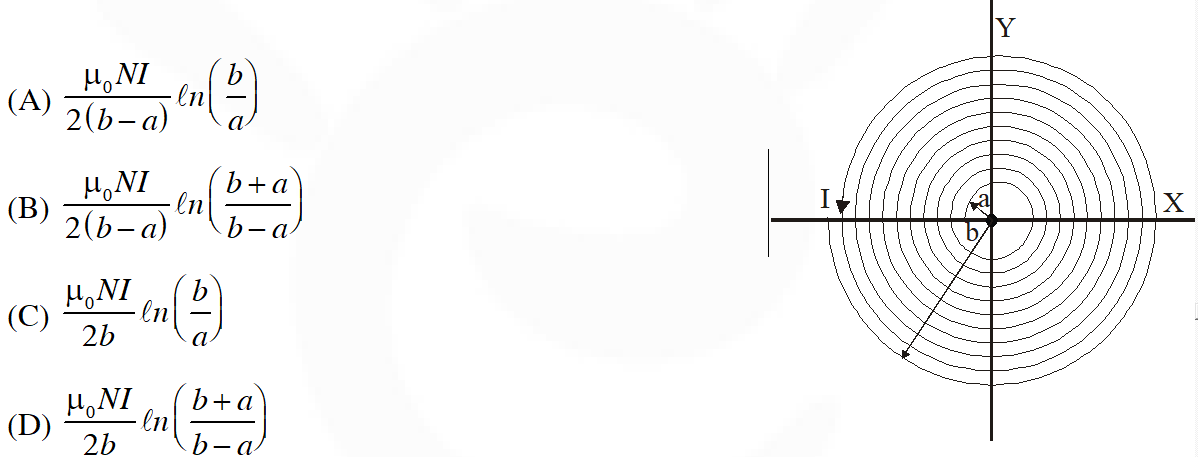[IIT-JEE 2011]
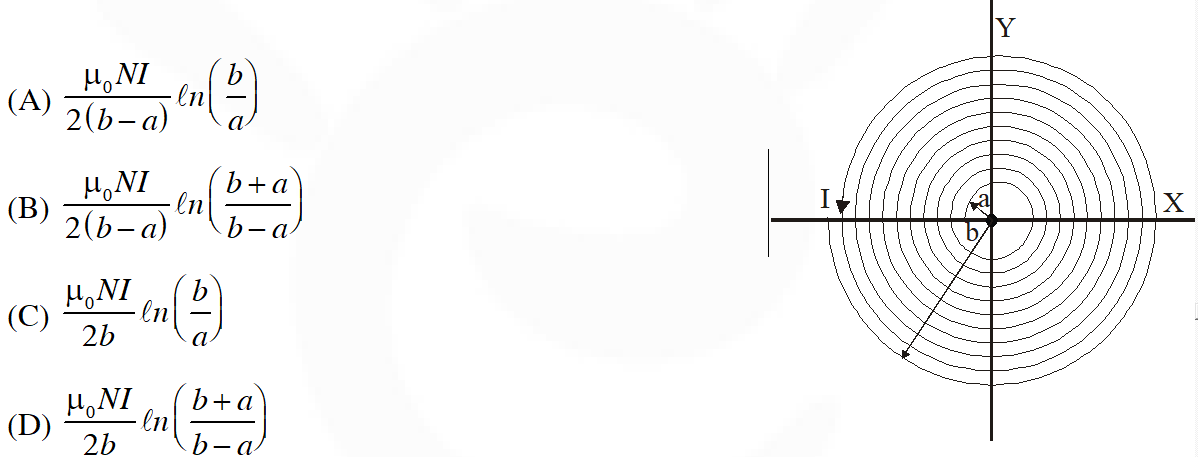[IIT-JEE 2011]
Ans. (A)
Taking an elemental strip of radius x and width dx.
Area of strip = $2 \pi \mathrm{x}$ dx
Number of turns through area $=\frac{N}{b-a} d x$
$\int d B=\int_{a}^{b} \frac{\mu_{0} \frac{N}{(b-a)} I d x}{2 x}=\frac{\mu_{0} N I \ell n\left(\frac{b}{a}\right)}{2(b-a)} |$
Q. Consider the motion of a positive point charge in a region where there are simultaneous uniform electric and magnetic fields $\vec{E}=E_{0} \hat{j}$ and $\vec{B}=B_{0} \hat{j}$ and . At time t =0, this charge has velocity in the x-y plane, making an angle $\theta$ with the x-axis. Which of the following option (s) is (are) correct for time t > 0?
(A) If $\theta=0^{\circ},$ the charge moves in a circular path in the $\mathrm{x}-\mathrm{z}$ plane.
(B) If $\theta=0^{\circ},$ the charge undergoes helical motion with constant pitch along the y-axis.
(C) If $\theta=10^{\circ},$ the charge undergoes helical motion with its pitch increasing with time, along the
$y$ -axis
(D) If $\theta=90^{\circ},$ the charge undergoes linear but accelerated motion along the $\mathrm{y}$ -axis
[IIT-JEE 2012]
Ans. (C,D)
Q. A cylindrical cavity of diameter a exists inside a cylinder of diameter
2a as shown in the figure. Both the cylinder and the cavity are infinitely long. A uniform current density J flows along the length. If the magnitude of the magnetic field at the point P is given by $\frac{N}{12} \mu_{0} a J$, then the value of N is
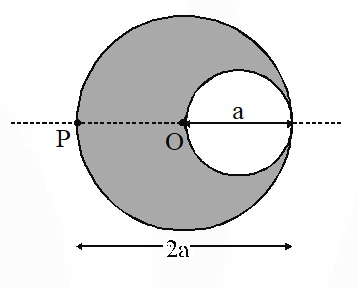[IIT-JEE 2012]
[IIT-JEE 2012]
Ans. (5)
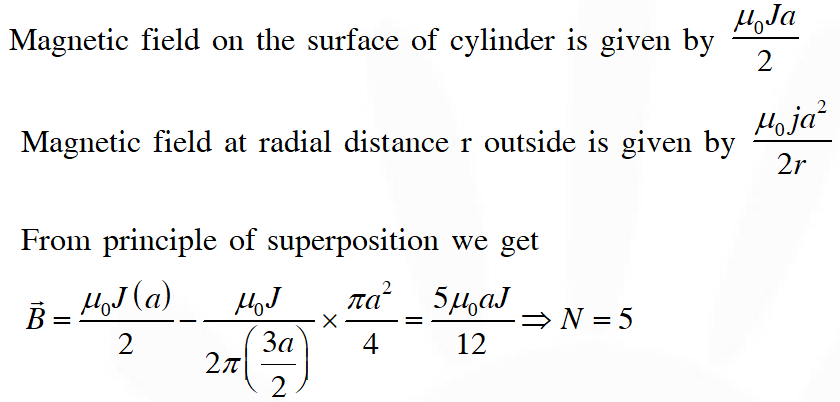
Q. An infinitely long hollow conducting cylinder with inner radius R/2 and outer radius R carries a uniform current density along its length. The magnitude of the magnetic field, $|\vec{B}|$ as a function of the radial distance r from the axis is best represented by
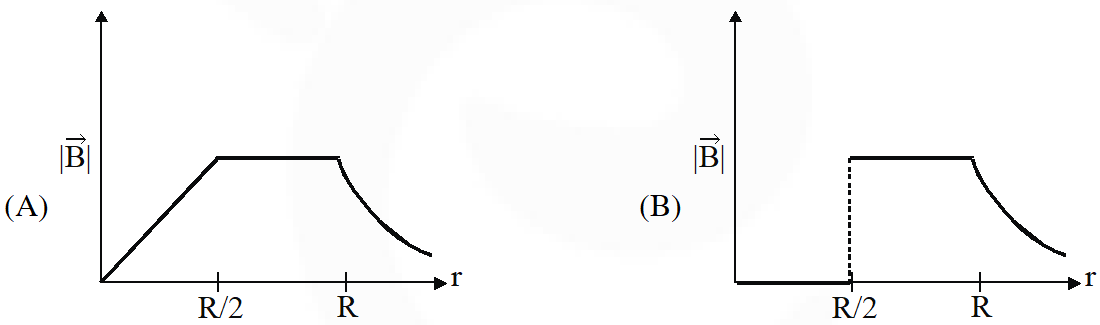
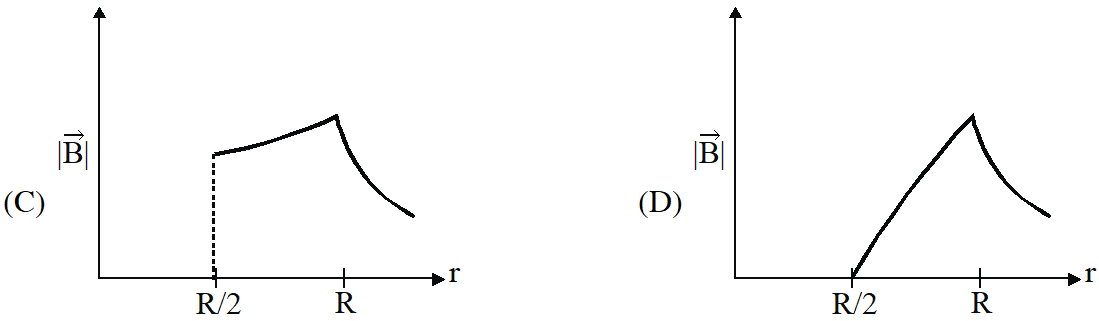[IIT-JEE 2012]
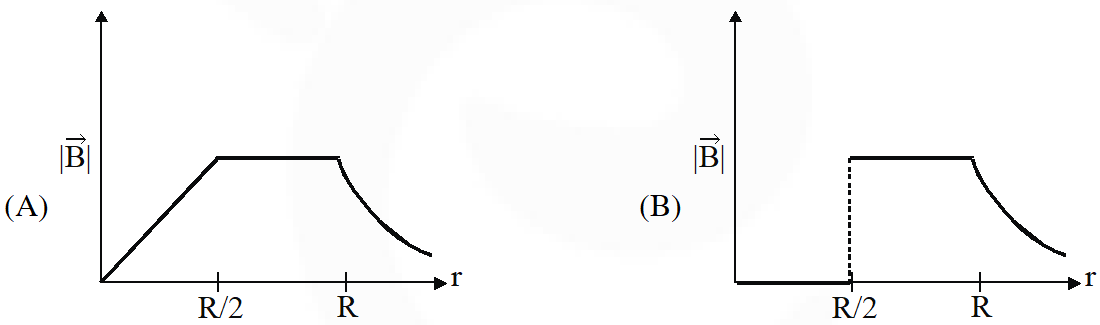
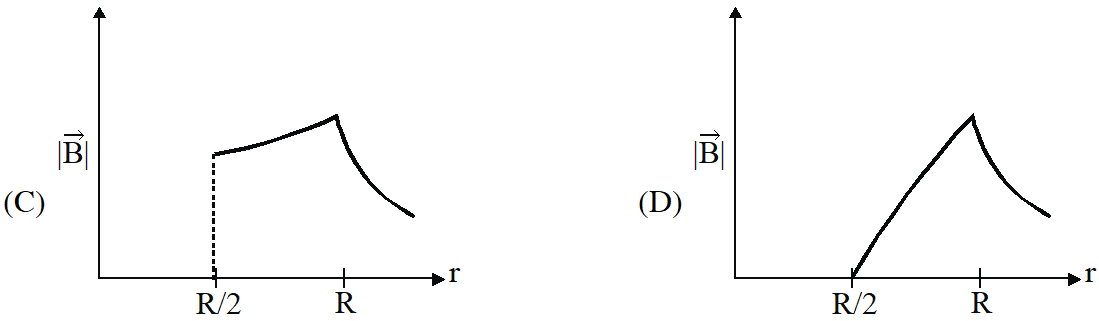[IIT-JEE 2012]
Ans. (D)
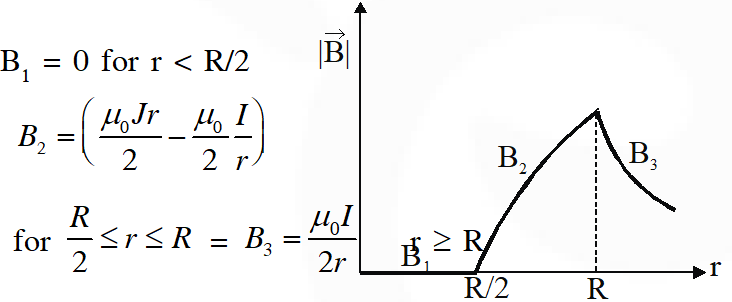
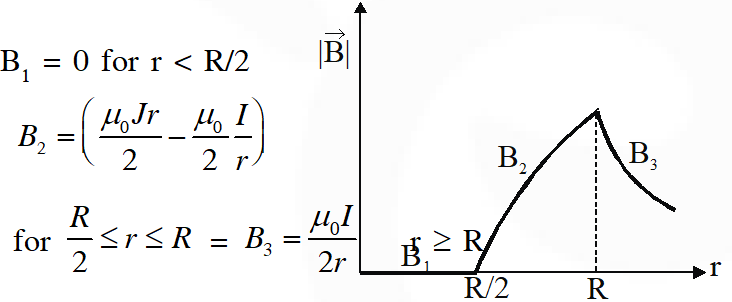
Q. A particle of mass M and positive charge Q, moving with a constant velocity $\overrightarrow{\mathrm{u}}_{1}=4 \hat{\mathrm{i}} \mathrm{ms}^{-1}$, enters a region of uniform static magnetic field normal to the x-y plane. The region of the magnetic field extends from x = 0 to x = L from all values of y. After passing through this region, the particle emerges on the other side after 10 milliseconds with a velocity $\overrightarrow{\mathrm{u}}_{2}=2(\sqrt{3 \hat{\mathrm{i}}}+\hat{\mathrm{j}}) \mathrm{ms}^{-1}$. The correct statements(s) is (are) :-
(A) The direction of the magnetic field is –z direction.
(B) The direction of the magnetic field is +z direction.
(C) The magnitude of the magnetic field $\frac{50 \pi \mathrm{M}}{3 \mathrm{Q}}$ units.
(D) The magnitude of the magnetic field is $\frac{100 \pi \mathrm{M}}{3 \mathrm{Q}}$ units.
[IIT-JEE 2013]
Ans. (A,C)
by direction of $\overrightarrow{\mathrm{F}} ;$ magnetic field is in $-\mathrm{z}$ direction
Time $=\frac{\theta}{\omega}=\frac{\pi / 6}{\mathrm{QB} / \mathrm{M}}=\frac{\mathrm{M} \pi}{6 \mathrm{QB}}$
$\Rightarrow \mathrm{B}=\frac{\mathrm{M} \pi}{6 \mathrm{Q}\left(10 \times 10^{-3}\right)}=\frac{50 \pi \mathrm{M}}{3 \mathrm{Q}}$
Q. A steady current I flows along an infinitely long hollow cylindrical conductor of radius R. This cylinder is placed coaxially inside an infinite solenoid of radius 2R. The solenoid has n turns per unit length and carries a steady current I. Consider a point P at a distance r from the common axis. The correct statement(s) is (are) :-
(A) In the region 0 < r < R, the magnetic field is non-zero
(B) In the region R < r < 2R, the magnetic field is along the common axis
(C) In the region R < r < 2R, the magnetic field is tangential to the circle of radius r, centredon the axis
(D) In the region r > 2R, the magnetic field is non-zero
Ans. (A,D)
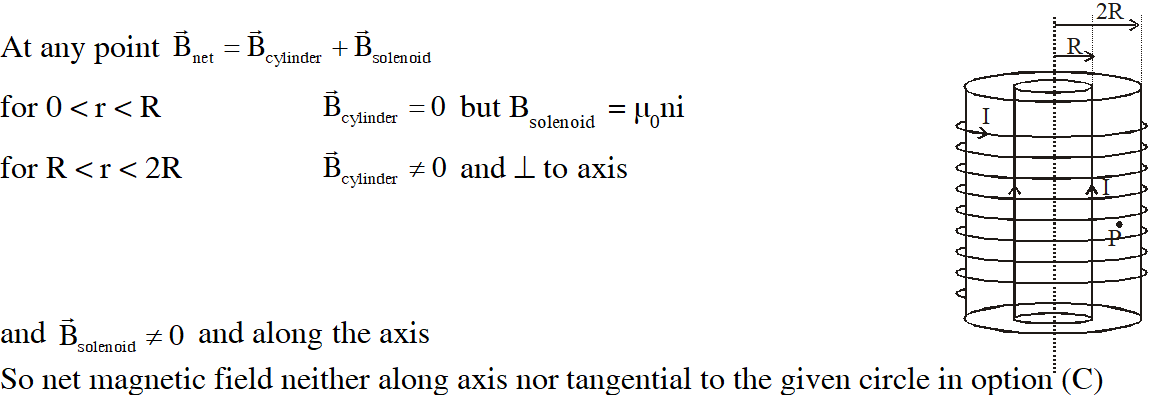
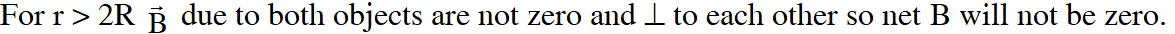
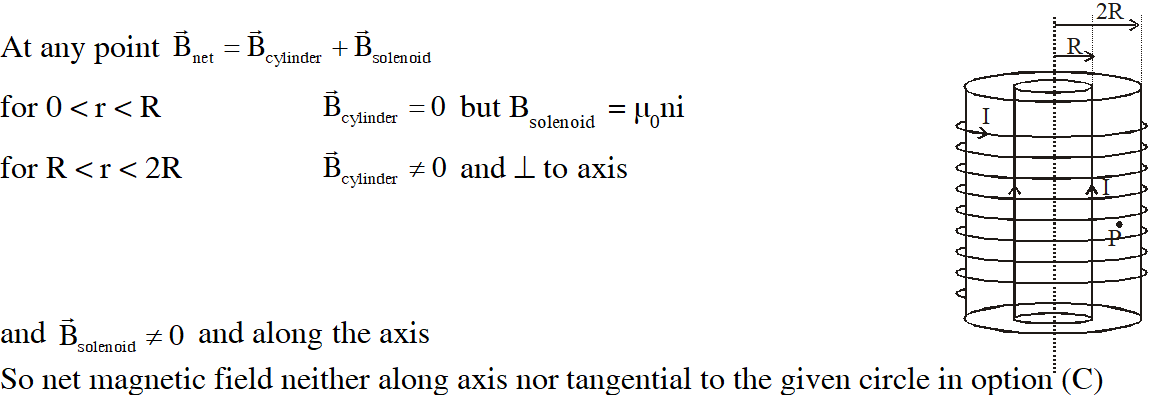
Q. Two parallel wires in the plane of the paper are distance $\mathrm{X}_{0}$ apart. A point charge is moving with speed u between the wires in the same plane at a distance $\mathbf{X}_{1}$ from one of the wires. When the wires carry current of magnitude I in the same direction, the radius of curvature of the path of the point charge is $\mathrm{R}_{1}$. In contrast, if the currents I in the two wires have directions opposite to each other, the radius of curvature of the path is $\mathrm{R}_{2}$. If $\frac{X_{0}}{X_{1}}=3$ , and value of $\frac{\mathrm{R}_{1}}{\mathrm{R}_{2}}$ is ?
[JEE-Advanced-2014]
Ans. 3
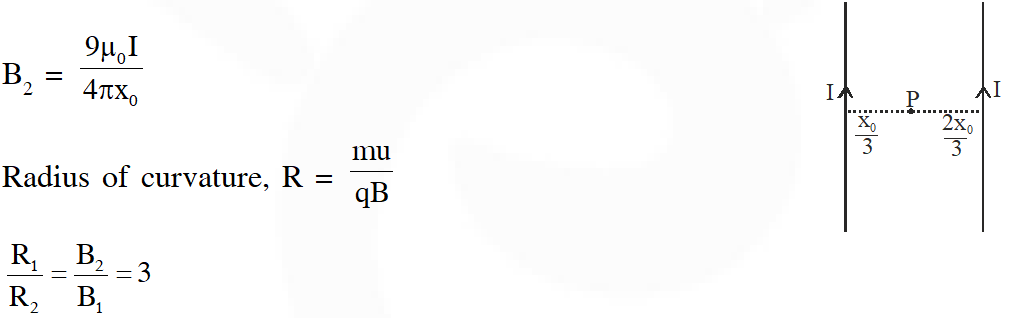
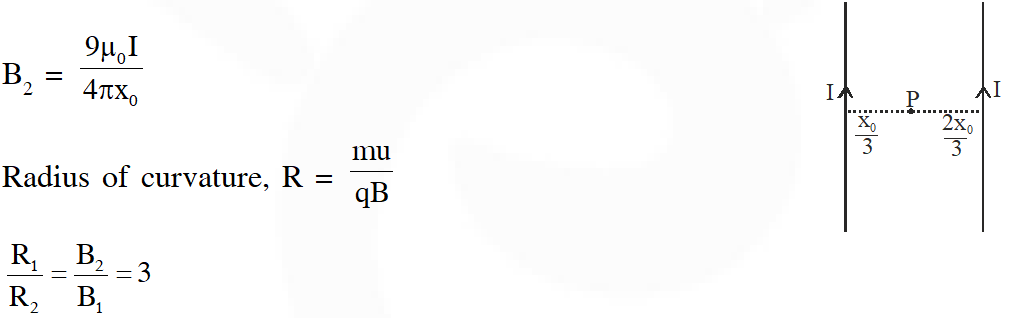
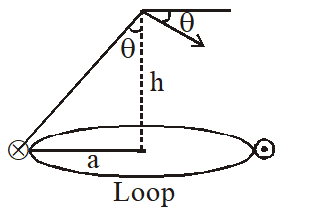
Q. When d $\approx$ a but wires are not touching the loop, it is found that the net magnetic field on the axis of the loop is zero at a height h above the loop. In that case
(A) current in wire 1 and wire 2 is the direction PQ and RS, respectively and h $\approx$ a
(B) current in wire 1 and wire 2 is the direction PQ and SR, respectively and h $\approx$ a
(C) current in wire 1 and wire 2 is the direction PQ and SR, respectively and h $\approx$ 1.2 a
(D) current in wire 1 and wire 2 is the direction PQ and RS, respectively and h $\approx$ 1.2 a
[JEE-Advanced-2014]
Ans. (C)
$\mathrm{B}_{\text {wire }}=\frac{\mu_{0} \mathrm{i}}{2 \pi \sqrt{\mathrm{a}^{2}+\mathrm{h}^{2}}} 2 \sin \theta$
$=\frac{\mu_{0} \mathrm{ia}}{\pi\left(\mathrm{a}^{2}+\mathrm{h}^{2}\right)}$
$\mathrm{B}_{\text {loop }}=\frac{\mu_{0} \mathrm{ia}^{2}}{2\left(\mathrm{a}^{2}+\mathrm{h}^{2}\right)^{3 / 2}}$
$\mathrm{B}_{\text {wire }}=\mathrm{B}_{\text {loop }}$
$\frac{\mu_{0} \mathrm{ia}}{\pi\left(\mathrm{a}^{2}+\mathrm{h}^{2}\right)}=\frac{\mu_{0} \mathrm{i} \mathrm{a}^{2}}{2\left(\mathrm{a}^{2}+\mathrm{h}^{2}\right)^{3 / 2}}$
$\sqrt{a^{2}+h^{2}}=\frac{\pi a}{2}$
$a^{2}+h^{2}=2.5 \mathrm{a}^{2}$
$\mathrm{h}^{2}=1.5 \mathrm{a}^{2}$
$\mathrm{h} \approx 1.2 \mathrm{a}$
$\mathrm{B}_{\text {wire }}=\frac{\mu_{0} \mathrm{i}}{2 \pi \sqrt{\mathrm{a}^{2}+\mathrm{h}^{2}}} 2 \sin \theta$
$=\frac{\mu_{0} \mathrm{ia}}{\pi\left(\mathrm{a}^{2}+\mathrm{h}^{2}\right)}$
$\mathrm{B}_{\text {loop }}=\frac{\mu_{0} \mathrm{ia}^{2}}{2\left(\mathrm{a}^{2}+\mathrm{h}^{2}\right)^{3 / 2}}$
$\mathrm{B}_{\text {wire }}=\mathrm{B}_{\text {loop }}$
$\frac{\mu_{0} \mathrm{ia}}{\pi\left(\mathrm{a}^{2}+\mathrm{h}^{2}\right)}=\frac{\mu_{0} \mathrm{i} \mathrm{a}^{2}}{2\left(\mathrm{a}^{2}+\mathrm{h}^{2}\right)^{3 / 2}}$
$\sqrt{a^{2}+h^{2}}=\frac{\pi a}{2}$
$a^{2}+h^{2}=2.5 \mathrm{a}^{2}$
$\mathrm{h}^{2}=1.5 \mathrm{a}^{2}$
$\mathrm{h} \approx 1.2 \mathrm{a}$
Q. Consider d >> a, and the loop is rotated about its diameter parallel to the wires by $30^{\circ}$ from the position shown in the figure. If the currents in the wires are in the opposite directions, the torque on the loop at its new position will be (assume that the net field due to the wires is constant over the loop)
(A) $\frac{\mu_{0} \mathrm{I}^{2} \mathrm{a}^{2}}{\mathrm{d}}$
(B) $\frac{\mu_{0} I^{2} a^{2}}{2 d}$
(C) $\frac{\sqrt{3} \mu_{0} \mathrm{I}^{2} \mathrm{a}^{2}}{\mathrm{d}}$
(D) $\frac{\sqrt{3} \mu_{0} \mathrm{I}^{2} \mathrm{a}^{2}}{2 \mathrm{d}}$
[JEE-Advanced-2014]
Ans. (B)
$|\vec{\tau}|=|\vec{M} \times \vec{B}|=M B \sin 30^{\circ}$
where $\mathrm{M}=\left(\pi \mathrm{a}^{2}\right) \mathrm{I}$ and $\mathrm{B}=2 \times \frac{\mu_{0} \mathrm{I}}{2 \pi \mathrm{d}}=\frac{\mu_{0} \mathrm{I}}{\pi \mathrm{d}}$ Therefore
$\tau=\left(\frac{\mu_{0} \mathrm{I}}{\pi \mathrm{d}}\right)\left(\pi \mathrm{a}^{2} \mathrm{I}\right)\left(\frac{1}{2}\right)=\frac{\mu_{0} \mathrm{I}^{2} \mathrm{a}^{2}}{2 \mathrm{d}}$
Q. A conductor (shown in the figure) carrying constant current I is kept in the x-y plane in a unfirom magnetic field $\overrightarrow{\mathrm{B}}$. If F is the magnitude of the total magnetic force acting on the conductor,
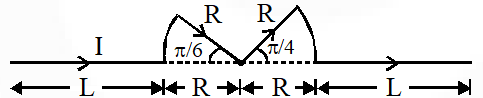(A) If $\overrightarrow{\mathrm{B}}$ is along $\hat{\mathrm{z}}, \mathrm{F} \propto(\mathrm{L}+\mathrm{R})$
(B) If $\overrightarrow{\mathrm{B}}$ is along $\hat{\mathrm{x}}, \mathrm{F}=0$
(C) If $\overrightarrow{\mathrm{B}}$ is along $\hat{\mathrm{y}}, \mathrm{F} \propto(\mathrm{L}+\mathrm{R})$
(D) If $\overrightarrow{\mathrm{B}}$ is along $\hat{\mathrm{z}}, \mathrm{F}=0$
[JEE-Advanced-2015]
(A) If $\overrightarrow{\mathrm{B}}$ is along $\hat{\mathrm{z}}, \mathrm{F} \propto(\mathrm{L}+\mathrm{R})$
(B) If $\overrightarrow{\mathrm{B}}$ is along $\hat{\mathrm{x}}, \mathrm{F}=0$
(C) If $\overrightarrow{\mathrm{B}}$ is along $\hat{\mathrm{y}}, \mathrm{F} \propto(\mathrm{L}+\mathrm{R})$
(D) If $\overrightarrow{\mathrm{B}}$ is along $\hat{\mathrm{z}}, \mathrm{F}=0$
[JEE-Advanced-2015]
Ans. (A,B,C)
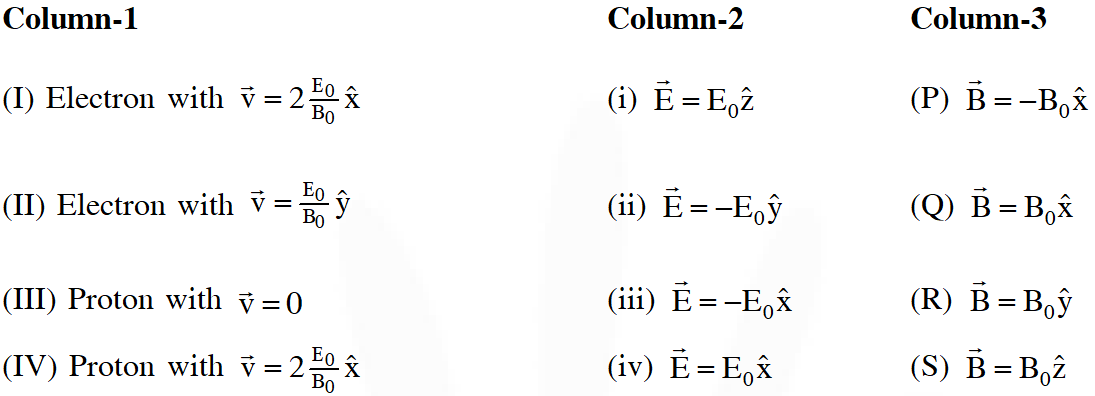
Q. In which case will the particle move in a straight line with constant velocity ?
(A) (II) (iii) (S) (B) (IV) (i) (S) (C) (III) (ii) (R) (D) (III) (iii) (P)
[JEE-Advanced-2017]
Ans. (A)
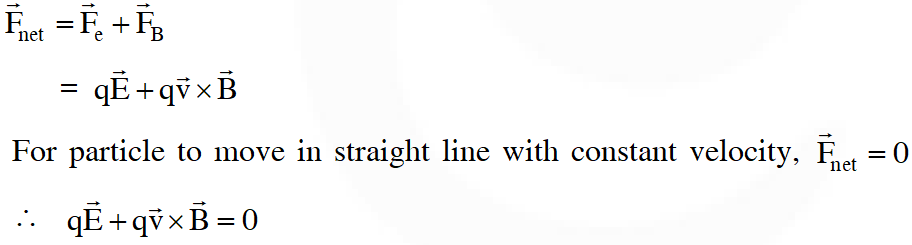
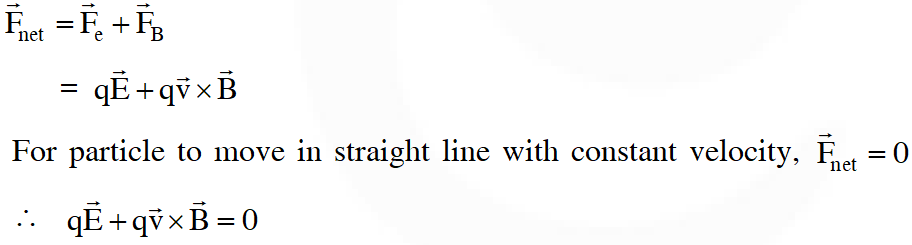
Q. In which case will the particle describe a helical path with axis along the positive z-direction ?
(A) (II) (ii) (R) (B) (IV) (ii) (R) (C) (IV) (i) (S) (D) (III) (iii) (P)
[JEE-Advanced-2017]
Ans. (C)
For path to be helix with axis along +ve z-direction, particle should experience a centripetal acceleration in x-y plane.
For the given set of options only option (C) satisfy the condition. Path is helical with increasing pitch.
Q. In which case would the particle move in a straight line along the negative direction of y-axis (i.e., move along $-\hat{y}$) ?
(A) (II) (iii) (S) (B) (IV) (i) (S) (C) (III) (ii) (R) (D) (III) (iii) (P)
[JEE-Advanced-2017]
Ans. (D)
For particle to move in -ve y-direction, either its velocity must be in –ve y-direction (if initial velocity $\neq$ 0) & force should be parallel to velocity or it must experience a net force in –ve y-direction only (if initial velocity = 0)
Q. A symmetric star shaped conducting wire loop is carrying a steady state current I as shown in the figure. The distance between the diametrically opposite vertices of the star is 4a. The magnitude of the magnetic field at the center of the loop is :
[JEE-Advanced-2017]
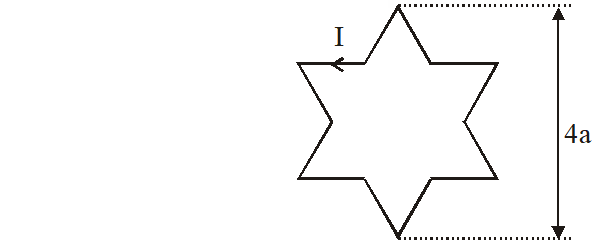
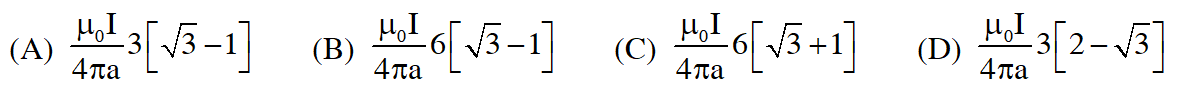[JEE-Advanced-2017]
Ans. (B)
The given points (1, 2, 3, 4, 5, 6) makes $360^{\circ}$ angle at 'O'. Hence angle made by vertices 1 & 2 with 'O' is $60^{\circ}$.
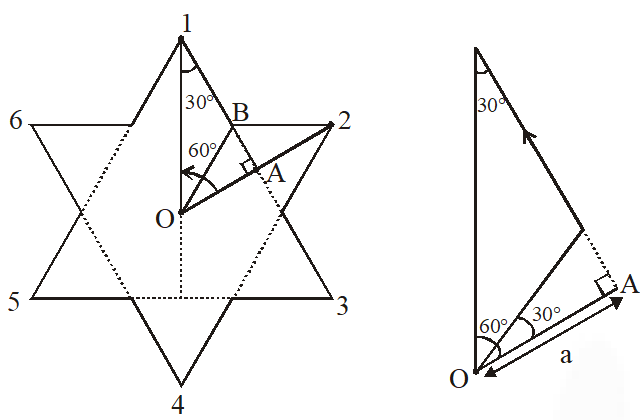Direction of magnetic field at 'O' due to each segment is same. Since it is symmetric star shape, magnitude will also be same.
Magnetic field due to section BC.
$\left(\mathrm{B}_{1}\right)=\frac{\mathrm{k} \mathrm{i}}{\mathrm{a}}(\sin (+60)-\sin 30)=\frac{\mathrm{ki}}{2 \mathrm{a}}(\sqrt{3}-1)$
$\mathrm{B}_{\mathrm{net}}=12 \times \mathrm{B}_{1}=\frac{6 \mathrm{ki}}{\mathrm{a}}(\sqrt{3}-1) \&\left(\mathrm{k}=\frac{\mu_{0}}{4 \pi}\right)$
Direction of magnetic field at 'O' due to each segment is same. Since it is symmetric star shape, magnitude will also be same.
Magnetic field due to section BC.
$\left(\mathrm{B}_{1}\right)=\frac{\mathrm{k} \mathrm{i}}{\mathrm{a}}(\sin (+60)-\sin 30)=\frac{\mathrm{ki}}{2 \mathrm{a}}(\sqrt{3}-1)$
$\mathrm{B}_{\mathrm{net}}=12 \times \mathrm{B}_{1}=\frac{6 \mathrm{ki}}{\mathrm{a}}(\sqrt{3}-1) \&\left(\mathrm{k}=\frac{\mu_{0}}{4 \pi}\right)$
Q. A uniform magnetic field B exists in the region between x = 0 and x = $\frac{3 \mathrm{R}}{2}$ (region 2 in the figure) pointing normally into the plane of the paper. A particle with charge +Q and momentum p directed along x-axis enters region 2 from region 1 at point $P_{1}$ (y = –R). Which of the following options(s) is/are correct ?
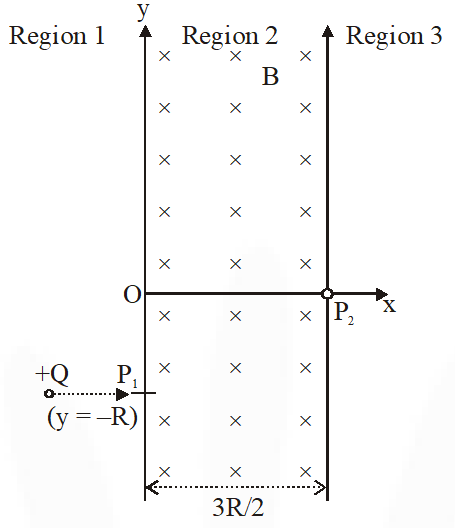(A) For $\mathrm{B}=\frac{8}{13} \frac{\mathrm{p}}{\mathrm{QR}}$, the particle will enter region 3 through the point $P_{2}$ on x-axis
(B) For $\mathrm{B}>\frac{2}{3} \frac{\mathrm{p}}{\mathrm{QR}}$, the particle will re-enter region 1
(C) For a fixed B, particle of same charge Q and same velocity v, the distance between the point $P_{1}$ and the point of re-entry into region 1 is inversely proportional to the mass of the particle.
(D) When the particle re-enters region 1 through the longest possible path in region 2, the magnitude of the chage in its linear momentum between point $P_{1}$ and the farthest point from y-axis is $\frac{\mathrm{p}}{\sqrt{2}}$.
[JEE-Advanced-2017]
(A) For $\mathrm{B}=\frac{8}{13} \frac{\mathrm{p}}{\mathrm{QR}}$, the particle will enter region 3 through the point $P_{2}$ on x-axis
(B) For $\mathrm{B}>\frac{2}{3} \frac{\mathrm{p}}{\mathrm{QR}}$, the particle will re-enter region 1
(C) For a fixed B, particle of same charge Q and same velocity v, the distance between the point $P_{1}$ and the point of re-entry into region 1 is inversely proportional to the mass of the particle.
(D) When the particle re-enters region 1 through the longest possible path in region 2, the magnitude of the chage in its linear momentum between point $P_{1}$ and the farthest point from y-axis is $\frac{\mathrm{p}}{\sqrt{2}}$.
[JEE-Advanced-2017]
Ans. (A,B)
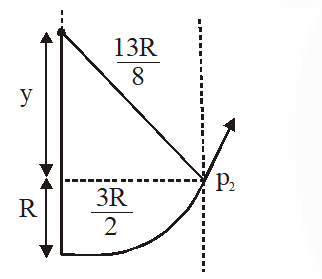For $\mathrm{B}=\fra
c{8}{13} \frac{\mathrm{p}}{\mathrm{QR}},$ radius of path
$\mathrm{R}^{\prime}=\frac{\mathrm{p}}{\mathrm{Q.B}}=\frac{\mathrm{p} \times 13 \mathrm{QR}}{\mathrm{Q} 8 \mathrm{p}}=\frac{13}{8} \mathrm{R}$
using pythagorous theorem, $\mathrm{y}=\frac{5 \mathrm{R}}{8}$
$\therefore$ particle will enter region 3 through point $\mathrm{P}_{2}$
for $\mathrm{B}>\frac{2}{3} \frac{\mathrm{p}}{\mathrm{QR}}$
Radius of path $<\frac{3 \mathrm{PQR}}{\mathrm{Q} 2 \mathrm{p}}=\frac{3}{2} \mathrm{R}$
$\therefore$ Particle will not enter in region $3 \&$ will re-enter region 1
charge in momentum = $\sqrt{2} \mathrm{p}$. When particle enters region 1 between entry point & farthest point from y-axis.
For $\mathrm{B}=\fra
c{8}{13} \frac{\mathrm{p}}{\mathrm{QR}},$ radius of path
$\mathrm{R}^{\prime}=\frac{\mathrm{p}}{\mathrm{Q.B}}=\frac{\mathrm{p} \times 13 \mathrm{QR}}{\mathrm{Q} 8 \mathrm{p}}=\frac{13}{8} \mathrm{R}$
using pythagorous theorem, $\mathrm{y}=\frac{5 \mathrm{R}}{8}$
$\therefore$ particle will enter region 3 through point $\mathrm{P}_{2}$
for $\mathrm{B}>\frac{2}{3} \frac{\mathrm{p}}{\mathrm{QR}}$
Radius of path $<\frac{3 \mathrm{PQR}}{\mathrm{Q} 2 \mathrm{p}}=\frac{3}{2} \mathrm{R}$
$\therefore$ Particle will not enter in region $3 \&$ will re-enter region 1
charge in momentum = $\sqrt{2} \mathrm{p}$. When particle enters region 1 between entry point & farthest point from y-axis.
Q. Two infinitely long straight wires lie in the xy-plane along the lines x = $\pm R$. The wire located at x = +R carries a constant current $\mathbf{I}_{1}$ and the wire located at x = –R carries a constant current $\mathrm{I}_{2}$. A circular loop of radius R is suspended with its centre at $(0,0, \sqrt{3} \mathrm{R})$ and in a plane parallel to the xy-plane. This loop carries a constant current I in the clockwise direction as seen from above the loop. The current in the wire is taken to be positive if it is in the $+\hat{j}$ direction. Which of the following statements regarding the magnetic field $\overrightarrow{\mathrm{B}}$ is (are) true ?
(A) If $\mathbf{I}_{1}$ = $\mathbf{I}_{2}$, then cannot be equal to zero at the origin (0, 0, 0)
(B) If $\mathbf{I}_{1}$ > 0 and $\mathbf{I}_{2}$ < 0, then can be equal to zero at the origin (0, 0, 0)
(C) If $\mathbf{I}_{1}$ < 0 and $\mathbf{I}_{2}$ > 0, then can be equal to zero at the origin (0, 0, 0)
(D) If $\mathbf{I}_{1}$ = $\mathbf{I}_{2}$, then the z-component of the magnetic field at the centre of the loop is $\left(-\frac{\mu_{0} I}{2 R}\right)$
[JEE-Advanced-2018]
Ans. (A,B,D)
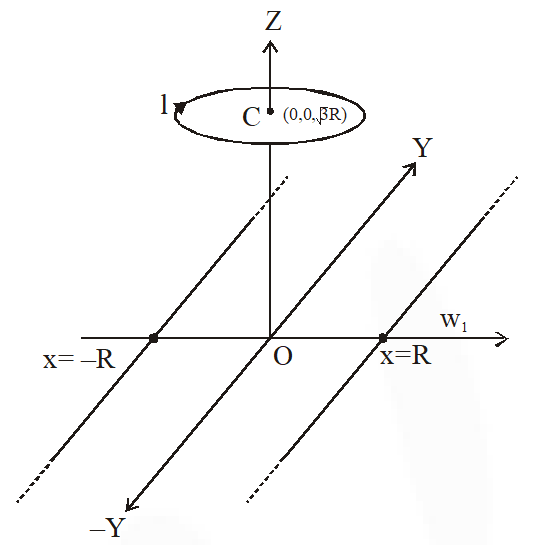
Q. In the x-y-plane, the region y > 0 has a uniform magnetic field $B_{1} \hat{k}$ and the region y < 0 has a another uniform magnetic field $B_{2} \hat{k}$. A positively charged particle is projected from the origin along the positive y-axis with speed $\mathrm{v}_{0}=\pi \mathrm{ms}^{-1}$ at $\mathrm{t}=0$ as shown in the figure. Neglect gravity in this problem. Let t = T be the time when the particle crosses the x-axis from below for the first time. If $\mathrm{B}_{2}=4 \mathrm{B}_{1}$, the average speed of the particle, in $\mathrm{ms}^{-1}$, along the x-axis in the time interval T is _______.
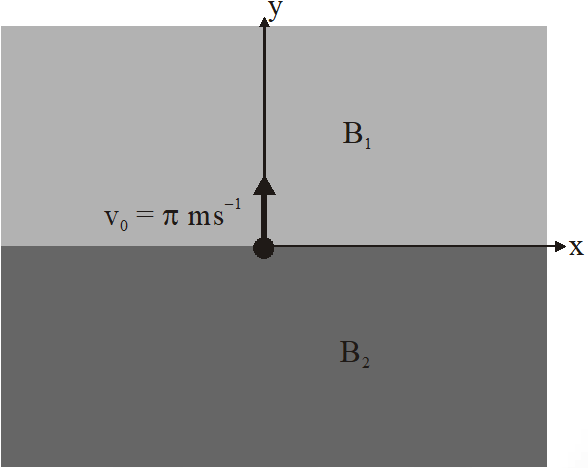[JEE-Advanced-2018]
[JEE-Advanced-2018]
Ans. 2
(1) Average speed along x-axis
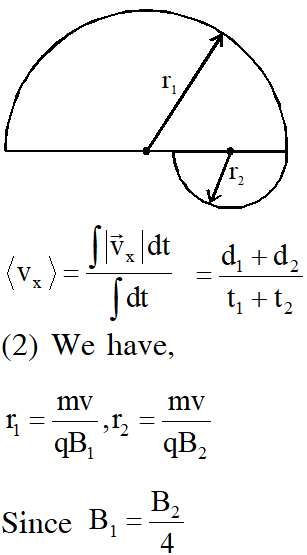
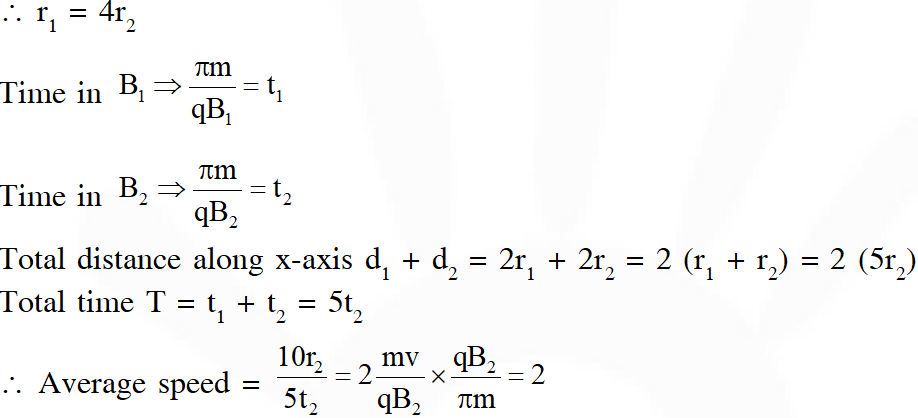
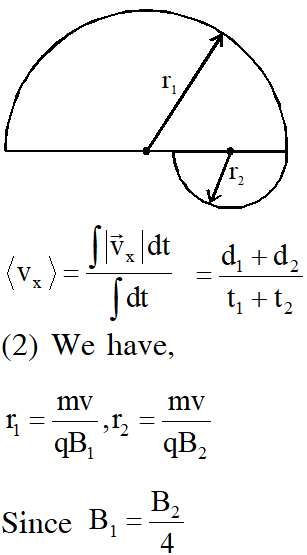
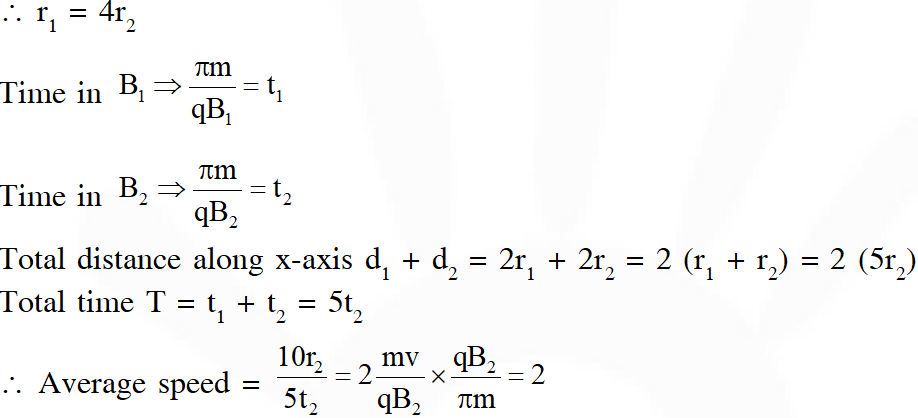
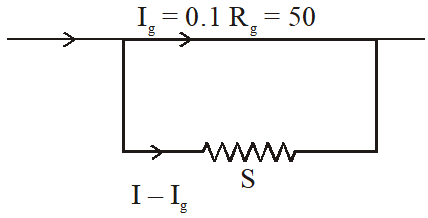
Q. A moving coil galvanometer has 50 turns and each turn has an area $2 \times 10^{-4} \mathrm{m}^{2}$. The magnetic field porduced by the magnet inside the galvanometer is 0.02 T. The torsional constant of the suspension wire is $10^{-4} \mathrm{N} \mathrm{m} \mathrm{rad}^{-1}$. When a current flows through the galvanometer, a full scale deflection occurs if the coil rotates by 0.2 rad. The resistance of the coil of the galvanometer is 50 $\Omega$. This galvanometer is to be converted into an ammeter capable of measuring current in the range 0 – 1.0 A. For this purpose, a shunt resistance is to be added in parallel to the galvanometer. The value of this shunt resistance, in ohms, is...........
[JEE-Advanced-2018]
Ans. 5.55
