JEE Main Previous Year Question of Math with Solutions are available at eSaral. Practicing JEE Main Previous Year Papers Questions of mathematics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
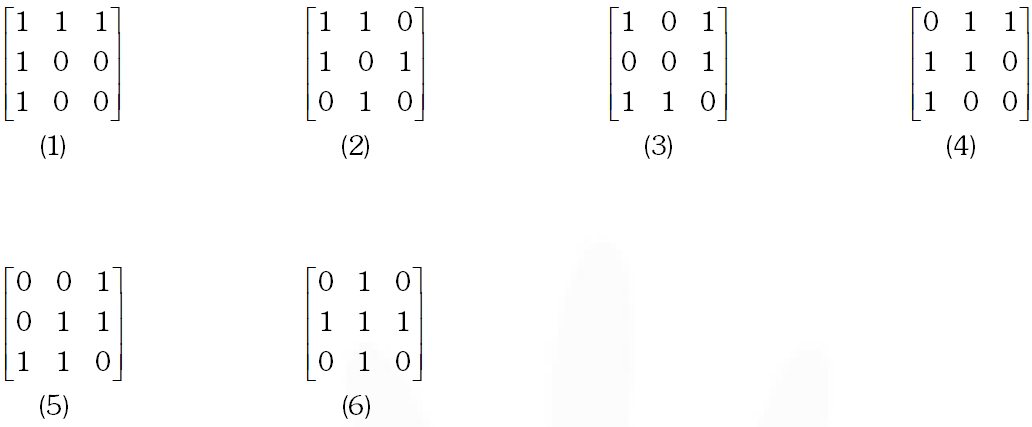
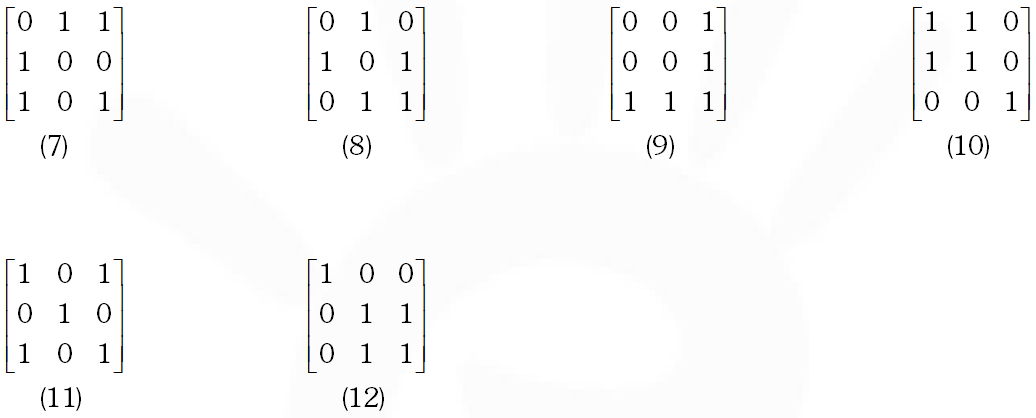
Q. Let A be the set of all 3 3 symmetric matrices all of whose entries are either 0 or 1. Five of these entries are 1 and four of them are 0.
(A) The number of matrices in A is –
(A) 12 (B) 6 (C) 9 (D) 3
(B) The number of matrices A in A for which the system of linear equations
$A\left[\begin{array}{l}{x} \\ {y} \\ {z}\end{array}\right]=\left[\begin{array}{l}{1} \\ {0} \\ {0}\end{array}\right]$ has a unique solution, is –
(A) less than 4
(B) at least 4 but less than 7
(C) at least 7 but less than 10
(D) at least 10
(C) The number of matrices A in A for which the system of linear equations $A\left[\begin{array}{l}{x} \\ {y} \\ {z}\end{array}\right]=\left[\begin{array}{l}{1} \\ {0} \\ {0}\end{array}\right]$ is inconsistent, is –
(A) 0 (B) more than 2 (C) 2 (D) 1
[JEE 2009, 4+4+4]
Ans. ( (A) A ,(b) B, (c) B )
Q. (A) The number of 3 3 matrices A whose entries are either 0 or 1 and for which the system $A\left[\begin{array}{l}{x} \\ {y} \\ {z}\end{array}\right]=\left[\begin{array}{l}{1} \\ {0} \\ {0}\end{array}\right]$ has exactly two distinct solutions, is
(A) 0 (B) $2^{9}-1$ (C) 168 (D) 2
(B) Let $\mathrm{k}$ be a positive real number and let $\mathrm{A}=\left[\begin{array}{ccc}{2 \mathrm{k}-1} & {2 \sqrt{\mathrm{k}}} & {2 \sqrt{\mathrm{k}}} \\ {2 \sqrt{\mathrm{k}}} & {1} & {-2 \mathrm{k}} \\ {-2 \sqrt{\mathrm{k}}} & {2 \mathrm{k}} & {-1}\end{array}\right]$ and
$\mathrm{B}=\left[\begin{array}{ccc}{0} & {2 \mathrm{k}-1} & {\sqrt{\mathrm{k}}} \\ {1-2 \mathrm{k}} & {0} & {2 \sqrt{\mathrm{k}}} \\ {-\sqrt{\mathrm{k}}} & {-2 \sqrt{\mathrm{k}}} & {0}\end{array}\right]$
If $\operatorname{det}(\operatorname{adj} \mathrm{A})+\operatorname{det}(\operatorname{adj} \mathrm{B})=10^{6},$ then $[\mathrm{k}]$ is equal to
[Note : adj M denotes the adjoint of a square matrix M and [k] denotes the largest integer less than or equal to k].
(C) Let p be an odd prime number and Tp be the following set of 2 2 matrices:
$\mathrm{T}_{\mathrm{p}}=\left\{\mathrm{A}=\left[\begin{array}{ll}{\mathrm{a}} & {\mathrm{b}} \\ {\mathrm{c}} & {\mathrm{a}}\end{array}\right]: \mathrm{a}, \mathrm{b}, \mathrm{c} \in\{0,1,2, \ldots \ldots, \mathrm{p}-1\}\right.$
(i) The number of $A$ in $T_{p}$ such that $A$ is either symmetric or skew symmetric or both, and det(A) divisible by p is –
(A) $(\mathrm{p}-1)^{2}$
(B) 2 (p – 1)
(C) $(p-1)^{2}+1$
(D) 2p –1
(ii) The number of $A$ in $T_{p}$ such that the trace of $A$ is not divisible by $p$
but det (A) is divisible by p is –
[Note : The trace of a matrix is the sum of its diagonal entries.]
(A) $(p-1)\left(p^{2}-p+1\right)$
(B) $\mathrm{p}^{3}-(\mathrm{p}-1)^{2}$
(C) $(p-1)^{2}$
(D) $(p-1)\left(p^{2}-2\right)$
(iii) The number of $A$ in $T_{p}$ such that $\operatorname{det}(A)$ is not divisible by $p$ is –
(A) $2 p^{2}$
(B) $\mathrm{p}^{3}-5 \mathrm{p}$
(C) $\mathrm{p}^{3}-3 \mathrm{p}$
(D) $\mathrm{p}^{3}-\mathrm{p}^{2}$
[JEE 2010, 3+3+3+3+3]
Ans. ($(a) A,(b) 4 ;(c)(i) D,(i i) C,(\text { iii }) D$)
For the matrix $(6),(9),(10),(11)$ the system of linear equation is incosistent.
(A) The given matrix system is a linear system in $\mathrm{x}, \mathrm{y}, \mathrm{z},$ hence it can have either a unique solution or no-solution or infinitely many solutions. It can never have exactly two distinct solutions.
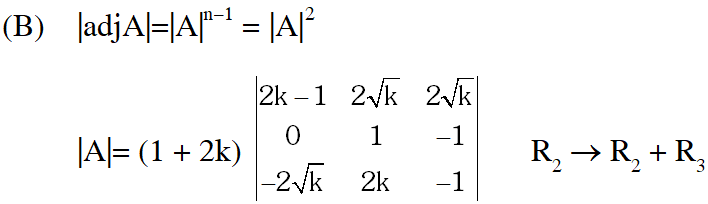
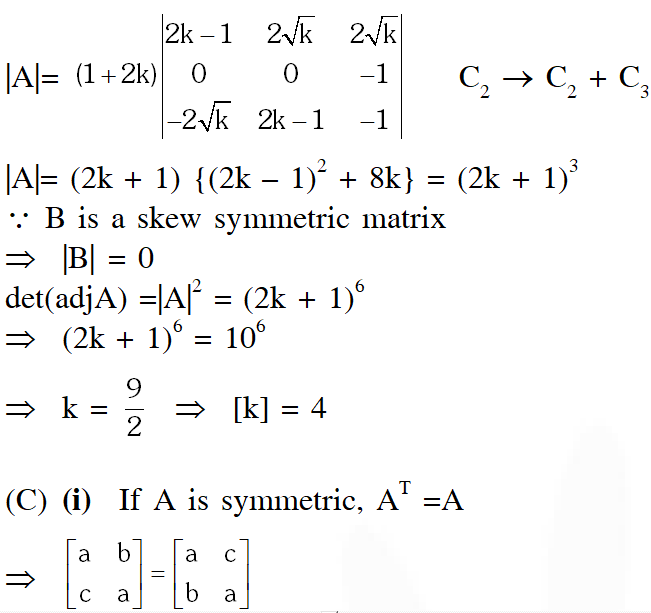
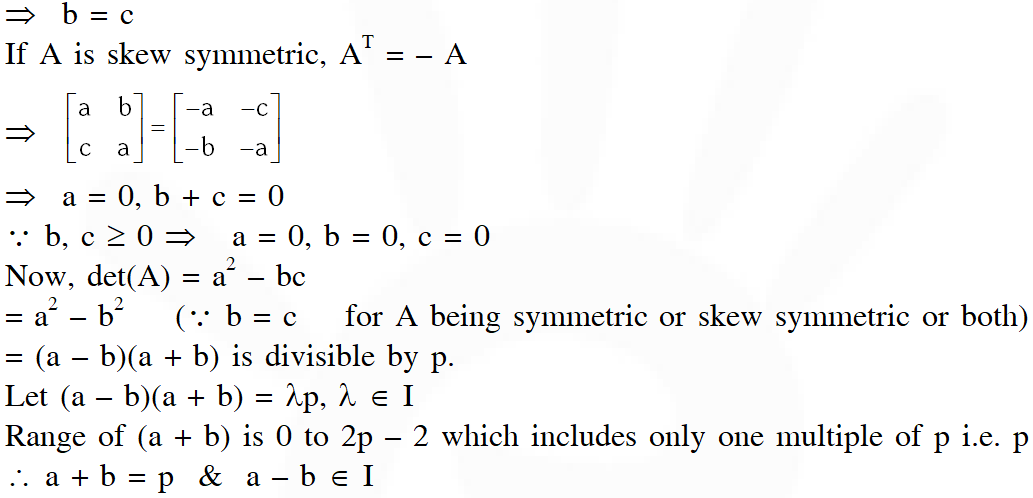
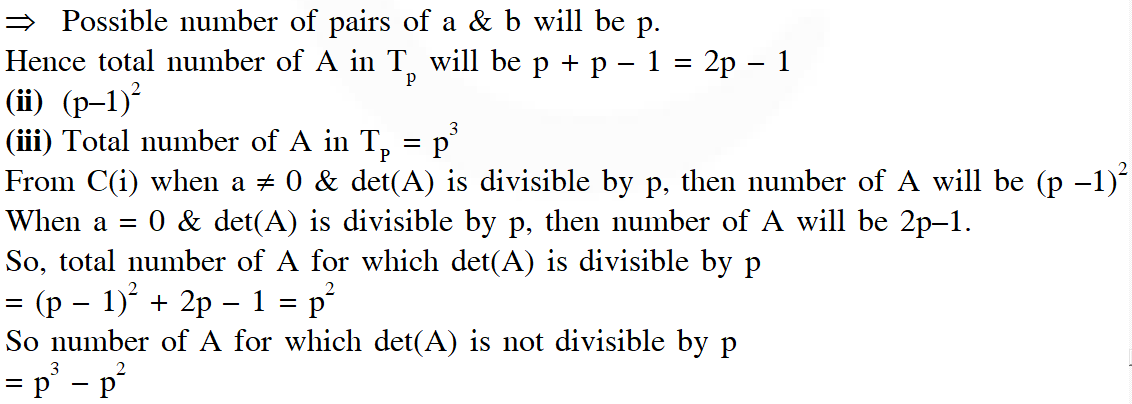
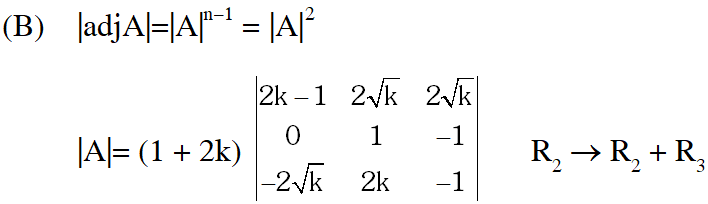
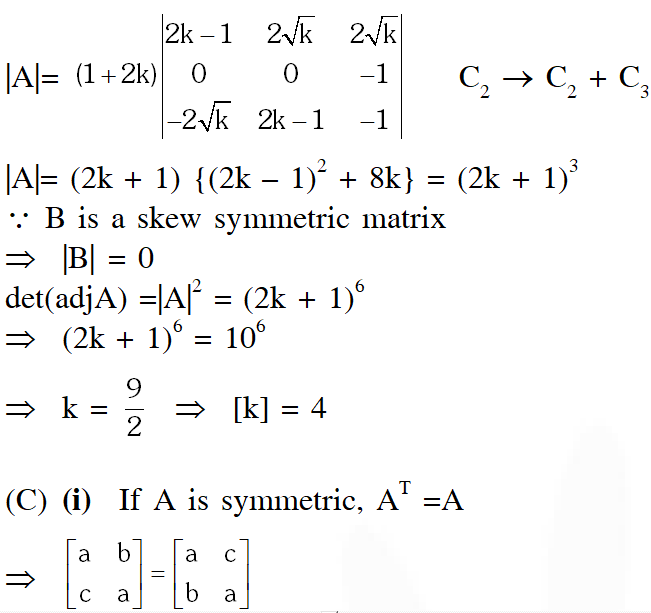
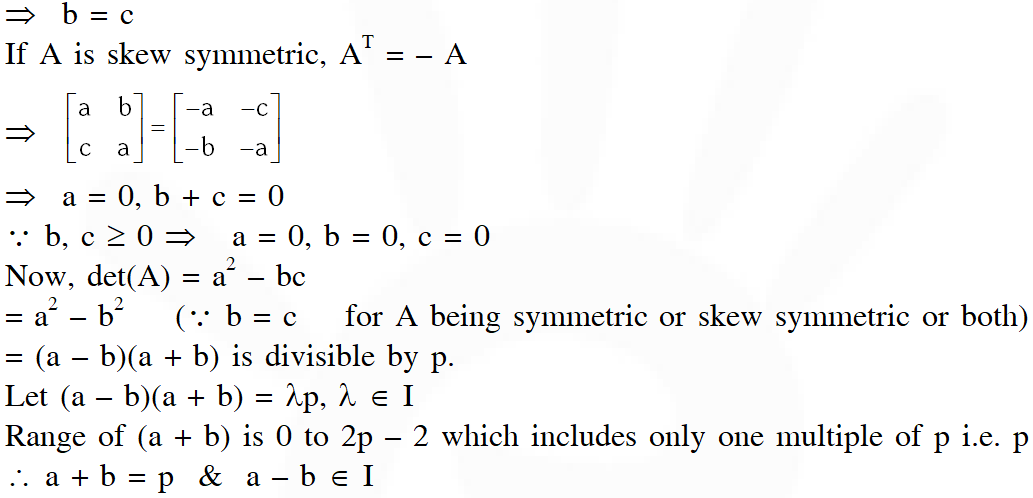
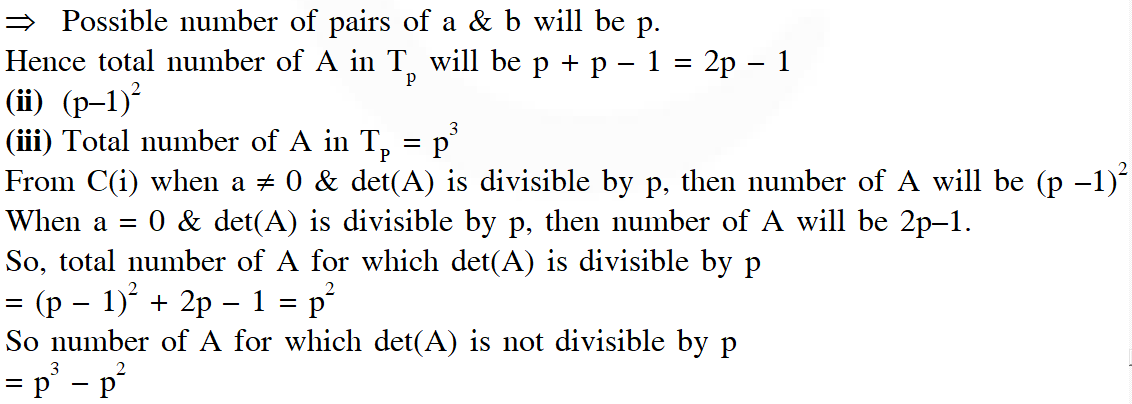
Q. Let $\mathrm{M}$ and $\mathrm{N}$ be two $3 \times 3$ non-singular skew-symmetric matrices such that $\mathrm{MN}=\mathrm{NM}$. If $\mathrm{P}^{\mathrm{T}}$ denotes the transpose of $\mathrm{P},$ then $\mathrm{M}^{2} \mathrm{N}^{2}\left(\mathrm{M}^{\mathrm{T}} \mathrm{N}\right)^{-1}\left(\mathrm{MN}^{-1}\right)^{\mathrm{T}}$ is equal to –
(A) $\mathbf{M}^{2}$
(B) $-N^{2}$
(C) $-M^{2}$
(D) MN
[JEE 2011, 4]
Ans. (Bonus)
(Comment : Although 3 3 skew symmetric matrices can never be non-singular. Therefore the information given in question is wrong. Now if we consider only non singular skew symmetric matrices M & N, then the solution is-)
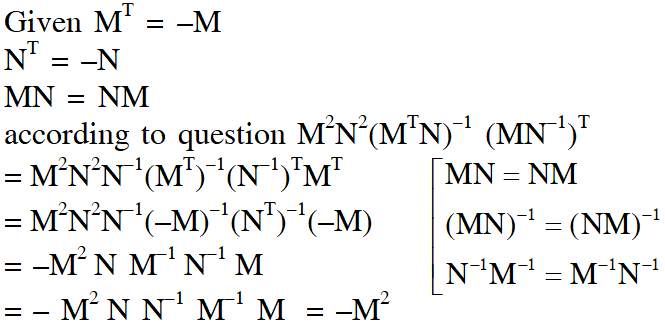
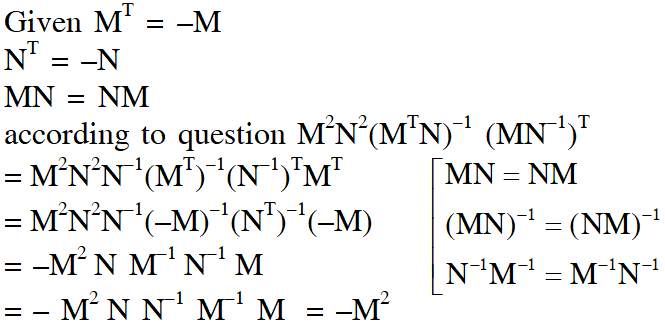
Q. Let $\omega \neq 1$ be a cube root of unity and $S$ be the set of all non-singular matrices of the form $\left[\begin{array}{lll}{1} & {a} & {b} \\ {\omega} & {1} & {c} \\ {\omega^{2}} & {\omega} & {1}\end{array}\right],$ where each of a,b and $c$ is either $\omega$ or $\omega^{2} .$ Then the number of distinct matrices in the set $\mathrm{S}$ is-
(A) 2 (B) 6 (C) 4 (D) 8
[JEE 2011, 3, (–1)]
Ans. (A)
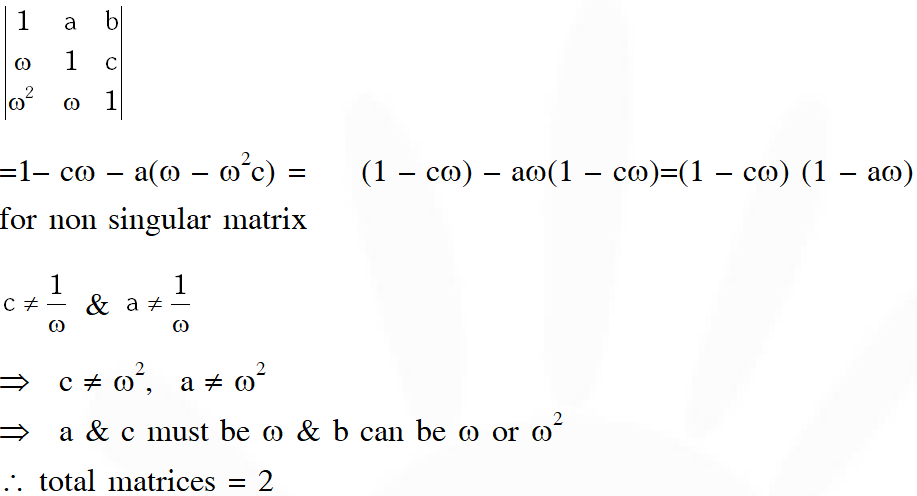
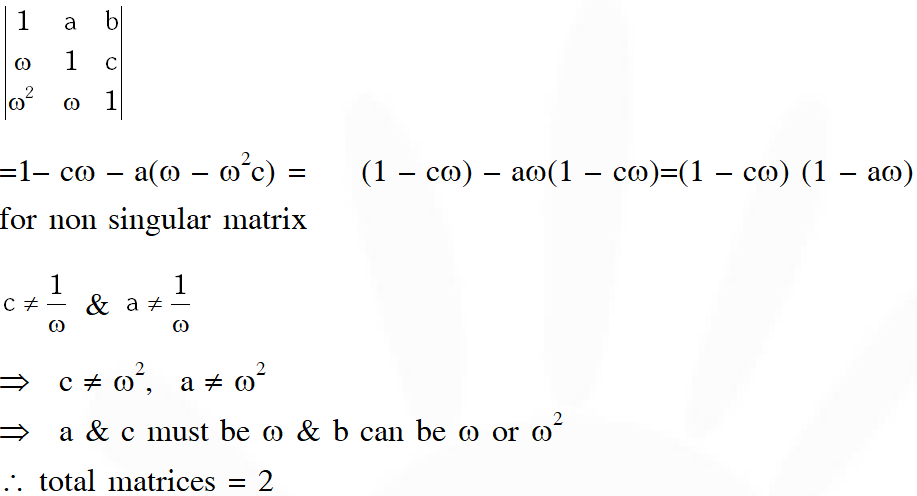
Q. Let M be 3 3 matrix satisfying $\mathbf{M}\left[\begin{array}{l}{0} \\ {1} \\ {0}\end{array}\right]=\left[\begin{array}{r}{-1} \\ {2} \\ {3}\end{array}\right], \mathbf{M}\left[\begin{array}{c}{1} \\ {-1} \\ {0}\end{array}\right]=\left[\begin{array}{r}{1} \\ {1} \\ {-1}\end{array}\right]$ and $\mathbf{M}\left[\begin{array}{l}{1} \\ {1} \\ {1}\end{array}\right]=\left[\begin{array}{c}{0} \\ {0} \\ {12}\end{array}\right]$ Then the sum of the diagonal entries of M is
[JEE 2011, 4]
Ans. 9
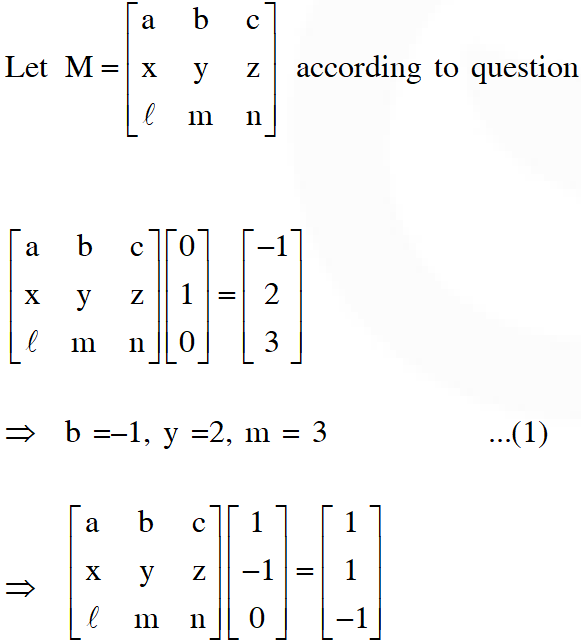
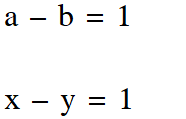
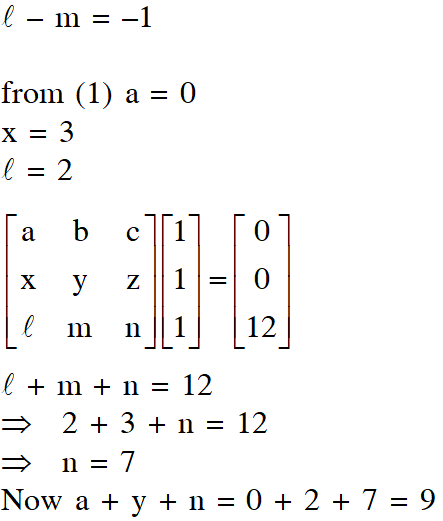
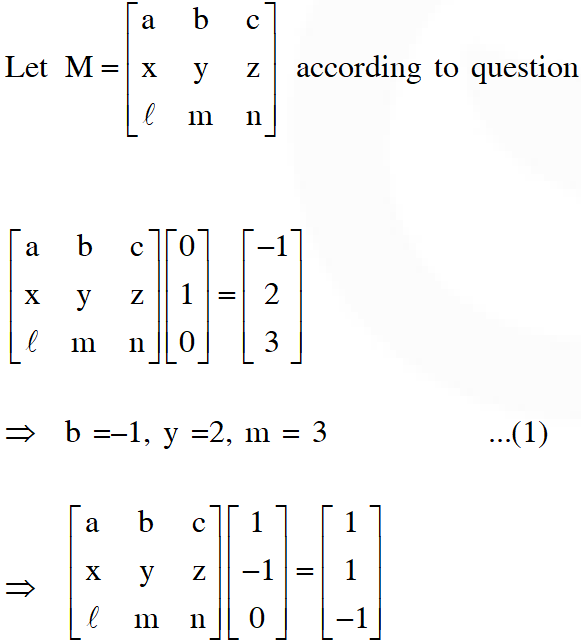
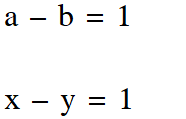
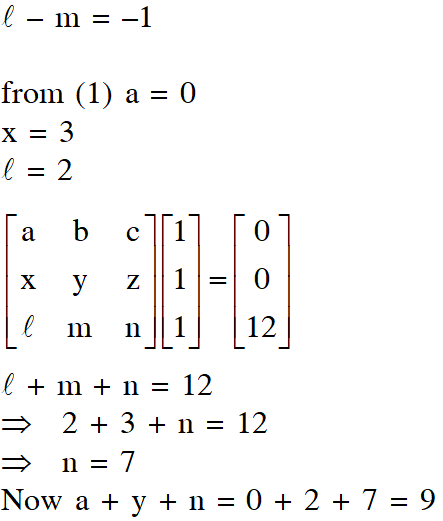
Q. Let $\mathrm{P}=\left[\mathrm{a}_{\mathrm{ij}}\right]$ be a $3 \times 3$ matrix and let $\mathrm{Q}=\left[\mathrm{b}_{\mathrm{ij}}\right],$ where $\mathrm{b}_{\mathrm{ij}}=2^{\mathrm{i}+\mathrm{j}} \mathrm{a}_{\mathrm{ij}}$ for $1 \leq \mathrm{i}, \mathrm{j} \leq 3$ If the determinant of $\mathrm{P}$ is $2,$ then the determinant of the matrix $\mathrm{Q}$ is –
(A) $2^{10}$
(B) $2^{11}$
(C) $2^{12}$
$(D) 2^{13}$
[JEE 2011, 4]
Ans. (D)
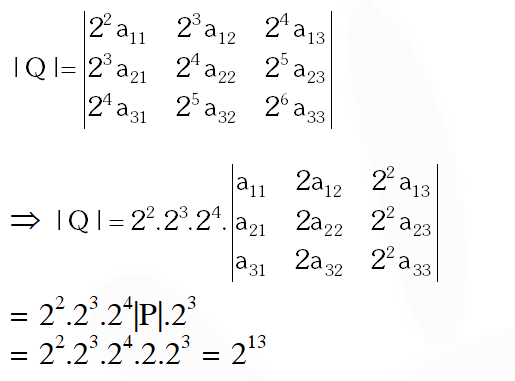
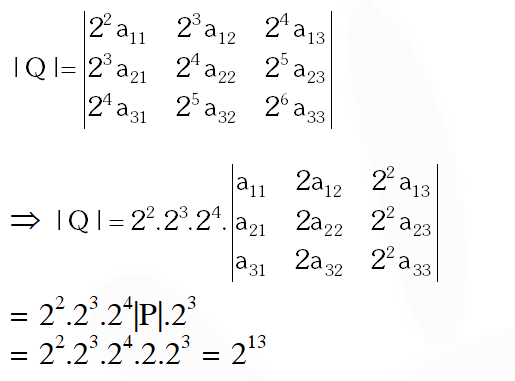
Q. If $\mathrm{P}$ is a $3 \times 3$ matrix such that $\mathrm{P}^{\mathrm{T}}=2 \mathrm{P}+\mathrm{I},$ where $\mathrm{P}^{\mathrm{T}}$ is the transpose of $\mathrm{P}$ and $\mathrm{I}$ is the $3 \times 3 \times 3$ identity matrix, then there exists a column matrix
$\mathrm{X}=\left[\begin{array}{l}{\mathrm{x}} \\ {\mathrm{y}} \\ {\mathrm{z}}\end{array}\right] \neq\left[\begin{array}{l}{0} \\ {0} \\ {0}\end{array}\right]$ such that
(A) $\mathrm{PX}=\left[\begin{array}{l}{0} \\ {0} \\ {0}\end{array}\right]$ (B) PX = X (C) PX = 2X (D) PX = –X
[JEE 2012, 3M, –1M]
Ans. (D)
$\mathrm{P}^{\mathrm{T}}=2 \mathrm{P}+\mathrm{I}$
$\Rightarrow \mathrm{P}=2 \mathrm{P}^{\mathrm{T}}+\mathrm{I}$
$\Rightarrow \mathrm{P}=2(2 \mathrm{P}+\mathrm{I})+\mathrm{I}$
$\Rightarrow P=4 P+3 I$
$\Rightarrow P=-I$
$\Rightarrow \mathrm{PX}=-\mathrm{X}$
Q. If the adjoint of a $3 \times 3$ matrix $\mathrm{P}$ is $\left[\begin{array}{ccc}{1} & {4} & {4} \\ {2} & {1} & {7} \\ {1} & {1} & {3}\end{array}\right],$ then the possible value(s) of the determinant of $\mathrm{P}$ is (are)
(A) –2 (B) –1 (C) 1 (D) 2
[JEE 2012, 4M]
Ans. (A,D)
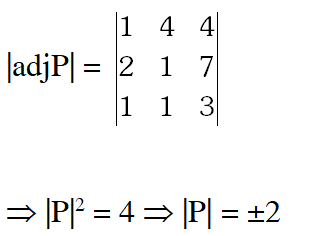
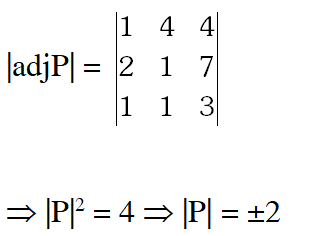
Q. For 3 3 matrices M and N, which of the following statement(s) is (are) NOT correct ?
(A) $\mathbf{N}^{\mathrm{T}} \mathbf{M}$ N is symmetric or skew symmetric, according as M is symmetric or
skew symmetric
(B) MN – NM is skew symmetric for all symmetric matrices M and N
(C) MN is symmetric for all symmetric matrices M and N
(D) (adj M) (adj N) = adj (M N) for all invertible matrices M and N
[JEE-Advanced 2013, 4, (–1)]
Ans. (C,D)
(A) $\mathrm{B}=\mathrm{N}^{\mathrm{T}} \mathrm{MN}$
$\mathrm{B}^{\mathrm{T}}=\left(\mathrm{N}^{\mathrm{T}} \mathrm{MN}\right)^{\mathrm{T}}=\mathrm{N}^{\mathrm{T}} \mathrm{M}^{\mathrm{T}} \mathrm{N}$
Now it depands on $\mathrm{M}$ if $\mathrm{M}=\mathrm{M}^{\mathrm{T}}$
So A is true
$(\mathrm{B}) \mathrm{B}=(\mathrm{MN}-\mathrm{NM})$
$\mathrm{B}=(\mathrm{MN}-\mathrm{NM})^{\mathrm{T}}$
$=\mathbf{N}^{\mathrm{T}} \mathbf{M}^{\mathrm{T}}-\mathbf{M}^{\mathrm{N}} \mathbf{N}^{\mathrm{T}}$
$=\mathrm{NM}-\mathrm{MN}=-(\mathrm{B})$ Skew symmetric
B is ture
$(\mathrm{C}) \mathrm{B}=\mathrm{MN}$
$\mathrm{B}^{\mathrm{T}}=(\mathrm{MN})^{\mathrm{T}}$
$\mathrm{B}^{\mathrm{T}}=\mathrm{N}^{\mathrm{T}} \mathrm{M}^{\mathrm{T}}$
$\mathrm{B}^{\mathrm{T}}=\mathrm{NM} \neq \mathrm{B}$ so wrong statement
(D) Obviousely wrong
because adj $(\mathrm{BA})=\operatorname{adj}(\mathrm{A}) \cdot \operatorname{adJ}(\mathrm{B})$
Q. Let M be a 2 2 symmetric matrix with integer entries. Then M is invertible if
(A) the first column of M is the transpose of the second row of M
(B) the second row of M is the transpose of the first column of M
(C) M is a diagonal matrix with nonzero entries in the main diagonal
(D) the product of entries in the main diagonal of M is not the square of an integer
[JEE(Advanced)-2014, 3]
Ans. (C,D)
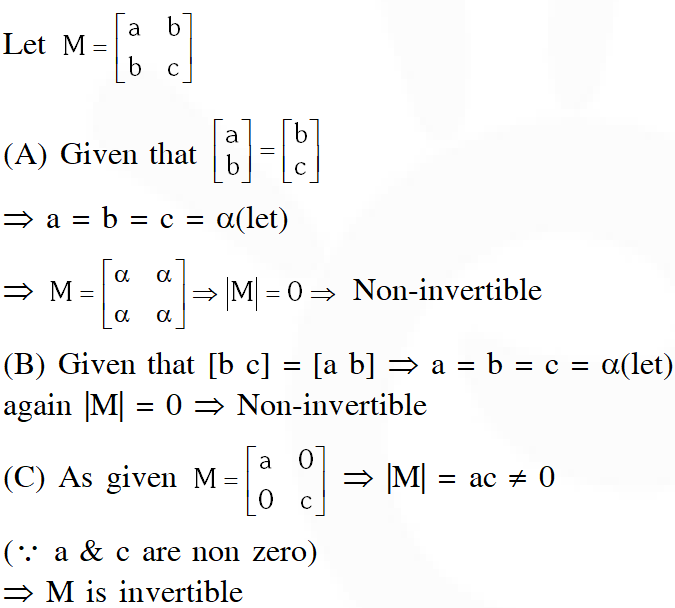
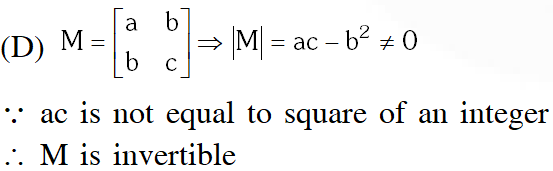
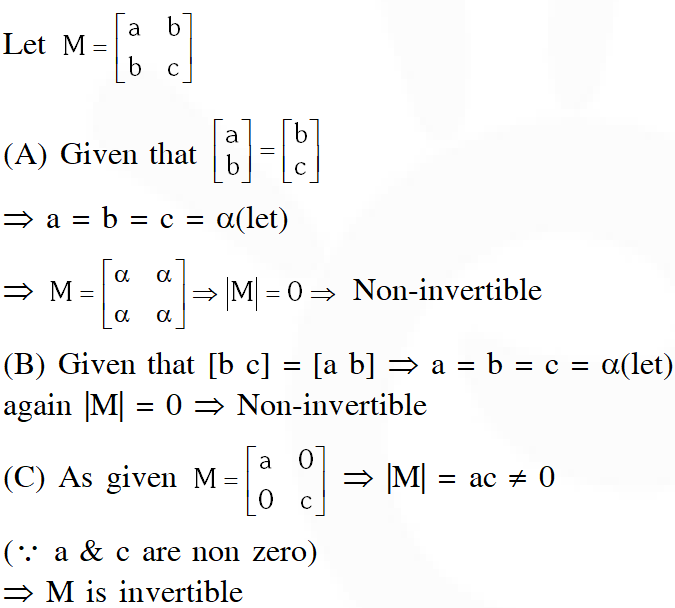
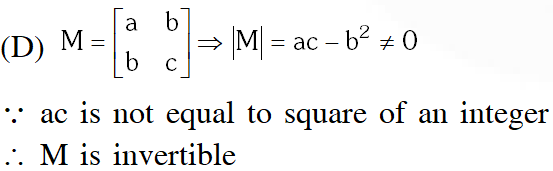
Q. Let $\mathrm{M}$ and $\mathrm{N}$ be two $3 \times 3$ matrices such that $\mathrm{MN}=\mathrm{NM}$. Further, if $\mathrm{M} \neq \mathrm{N}^{2}$ and $\mathrm{M}^{2}=$ $\mathrm{N}^{4},$ then
(A) determinant of $\left(\mathrm{M}^{2}+\mathrm{MN}^{2}\right)$ is 0
(B) there is a $3 \times 3$ non-zero matrix $\mathrm{U}$ such that $\left(\mathrm{M}^{2}+\mathrm{MN}^{2}\right) \mathrm{U}$ is zero Matrix
(C) determinant of $\left(\mathrm{M}^{2}+\mathrm{MN}^{2}\right) \geq 1$
(D) for a $3 \times 3$ matrix $\mathrm{U},$ if $\left(\mathrm{M}^{2}+\mathrm{MN}^{2}\right)$ U equals the zero matrix then $\mathrm{U}$ is the zero matrix
[JEE(Advanced)-2014, 3]
Ans. (A,B)
$\mathrm{M}^{2}=\mathrm{N}^{4}$
$\mathrm{M}^{2}=\mathrm{N}^{4}=0(\therefore \mathrm{MN}=\mathrm{NM})$
$\left(\mathrm{M}+\mathrm{N}^{2}\right)\left(\mathrm{M}-\mathrm{N}^{2}\right)=0$
So $\left(\mathrm{M}+\mathrm{N}^{2}\right)=0$
$\mathrm{Now} \mathrm{M} \cdot\left(\mathrm{M}+\mathrm{N}^{2}\right)=0$
$\mathrm{M}^{2}+\mathrm{MN}^{2}=0$
$\left|\mathrm{M}^{2}+\mathrm{MN}^{2}\right|=0$
Option A is right So we know $A \cdot B=0$
when $\mathrm{B} \neq 0$
$\Rightarrow(\mathrm{A})=0$
So in $\mathrm{U}\left(\mathrm{M}^{2}+\mathrm{MN}^{2}\right) \mathrm{U}=0$
Because $\mathrm{U} \neq 0$ But $\left|\mathrm{M}^{2}+\mathrm{MN}^{2}\right|=0$
So option $\mathrm{B}$ is also right
Q. Let X and Y be two arbitrary, 3 3, non-zero, skew-symmetric matrices and Z be an arbitrary 3 × 3, non-zero, symmetric matrix. Then which of the following matrices is (are) skew symmetric ?
(A) $\mathrm{Y}^{3} \mathrm{Z}^{4}-\mathrm{Z}^{4} \mathrm{Y}^{3}$
(B) $\mathrm{X}^{44}+\mathrm{Y}^{44}$
(C) $\mathrm{X}^{4} \mathrm{Z}^{3}-\mathrm{Z}^{3} \mathrm{X}^{4}$
(D) $\mathrm{X}^{23}+\mathrm{Y}^{23}$
[JEE(Advanced)-2015, 4M, –2M]
Ans. (C,D)
$\mathrm{x}^{\mathrm{T}}=-\mathrm{x}, \mathrm{y}^{\mathrm{T}}=-\mathrm{y}, \mathrm{z}^{\mathrm{T}}=\mathrm{z}$
(A) Let $P=y^{3} z^{4}-z^{4} y^{3}$
$\mathrm{P}^{\mathrm{T}}=\left(\mathrm{y}^{3} \mathrm{z}^{4}\right)^{\mathrm{T}}-\left(\mathrm{z}^{4} \mathrm{y}^{3}\right)^{\mathrm{T}}$
$=-z^{4} y^{3}+y^{3} z^{4}=P \Rightarrow$ symmetric
(B) $\quad$ Let $\mathrm{P}=\mathrm{x}^{44}+\mathrm{y}^{44}$
$\mathrm{P}^{\mathrm{T}}=\left(\mathrm{X}^{44}\right)^{\mathrm{T}}+\left(\mathrm{y}^{44}\right)^{\mathrm{T}}=\mathrm{P} \Rightarrow$ symmetric
(C) Let $P=x^{4} z^{3}-z^{3} x^{4}$
$\mathrm{P}^{\mathrm{T}}=\left(\mathrm{z}^{3}\right)^{\mathrm{T}}\left(\mathrm{x}^{4}\right)^{\mathrm{T}}-\left(\mathrm{x}^{4}\right)^{\mathrm{T}}\left(\mathrm{z}^{3}\right)^{\mathrm{T}}$
$=\mathrm{z}^{3} \mathrm{x}^{4}-\mathrm{x}^{4} \mathrm{z}^{3}=-\mathrm{P} \Rightarrow$ skew symmetric
(D) Let $P=x^{23}+y^{23}$ $\mathrm{P}^{\mathrm{T}}=-\mathrm{x}^{23}-\mathrm{y}^{23}=-\mathrm{P} \Rightarrow$ skew symmetric
Q. Let $P=\left[\begin{array}{ccc}{3} & {-1} & {-2} \\ {2} & {0} & {\alpha} \\ {3} & {-5} & {0}\end{array}\right],$ where $\alpha \in R,$ Suppose $Q=\left[q_{i j}\right]$ is a matrix such that $P Q=k I$ where $\mathrm{k} \in \mathrm{R}, \mathrm{k} \neq 0$ and $\mathrm{I}$ is the identity matrix of order $3 .$ If $\mathrm{q}_{23}=-\frac{\mathrm{k}}{8}$ and $\operatorname{det}(\mathrm{Q})=\frac{\mathrm{k}^{2}}{2}$ then-
(A) = 0, k = 8
(B) $4 \alpha-k+8=0$
(C) $\operatorname{det}(\operatorname{Padj}(\mathrm{Q}))=2^{9}$
(D) det(Qadj(P)) = $2^{13}$
[JEE(Advanced)-2016]
Ans. (B,C)
$\mathrm{PQ}=\mathrm{kI}$
$|\mathrm{P}| \cdot|\mathrm{Q}|=\mathrm{k}^{3} \Rightarrow|\mathrm{P}|=2 \mathrm{k} \neq 0 \Rightarrow \mathrm{P}$ is an invertible matrix
$\because \mathrm{PQ}=\mathrm{kI}$
$\therefore \mathrm{Q}=\mathrm{k} \mathrm{P}^{-1} \mathrm{I}$
$\therefore \mathrm{Q}=\frac{\mathrm{adj.P}}{2}$
$\because \mathrm{q}_{23}=-\frac{\mathrm{k}}{8}$
$\therefore \frac{-(3 \alpha+4)}{2}=-\frac{k}{8} \Rightarrow k=4$
$\therefore|\mathrm{P}|=2 \mathrm{k} \Rightarrow \mathrm{k}=10+6 \alpha \ldots(\mathrm{i})$
Put value of $k$ in (i).. we get $\alpha=-1$
$\therefore 4 \alpha-k+8=0$
$\& \operatorname{det}(\mathrm{P}(\mathrm{adj} . \mathrm{Q}))=|\mathrm{P}||\operatorname{adj} . \mathrm{Q}|=2 \mathrm{k} \cdot\left(\frac{\mathrm{k}^{2}}{2}\right)^{2}=\frac{\mathrm{k}^{5}}{2}=2^{9}$
Q. Let $P=\left[\begin{array}{lll}{1} & {0} & {0} \\ {4} & {1} & {0} \\ {16} & {4} & {1}\end{array}\right]$ and $I$ be the identity matrix of order $3 .$ If $Q=\left[q_{i j}\right]$ is a matrix such that $\mathrm{P}^{50}-\mathrm{Q}=\mathrm{I},$ then $\frac{\mathrm{q}_{31}+\mathrm{q}_{32}}{\mathrm{q}_{21}}$ equals
(A) 52 (B) 103 (C) 201 (D) 205
[JEE(Advanced)-2016]
Ans. (A)
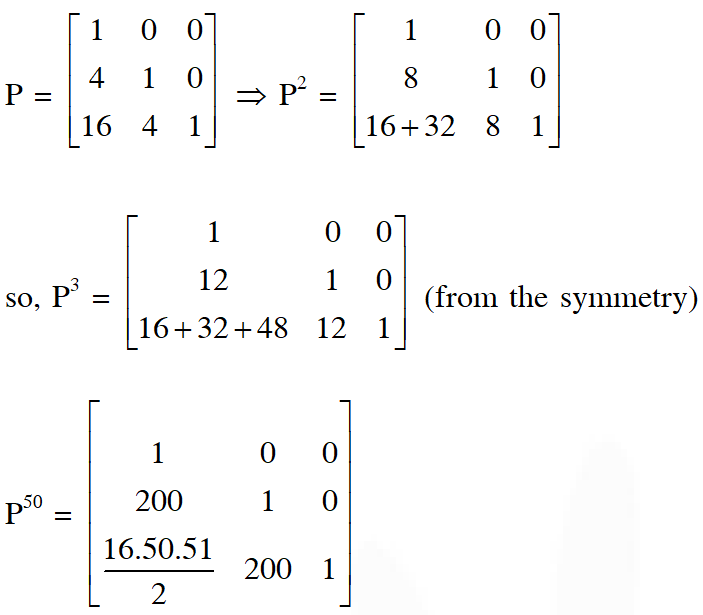
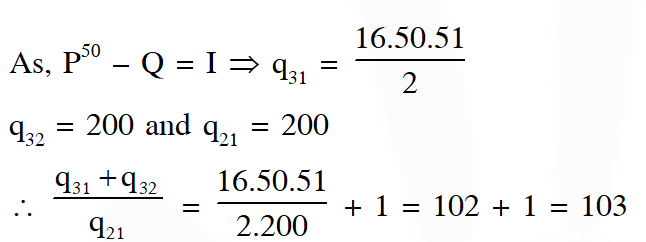
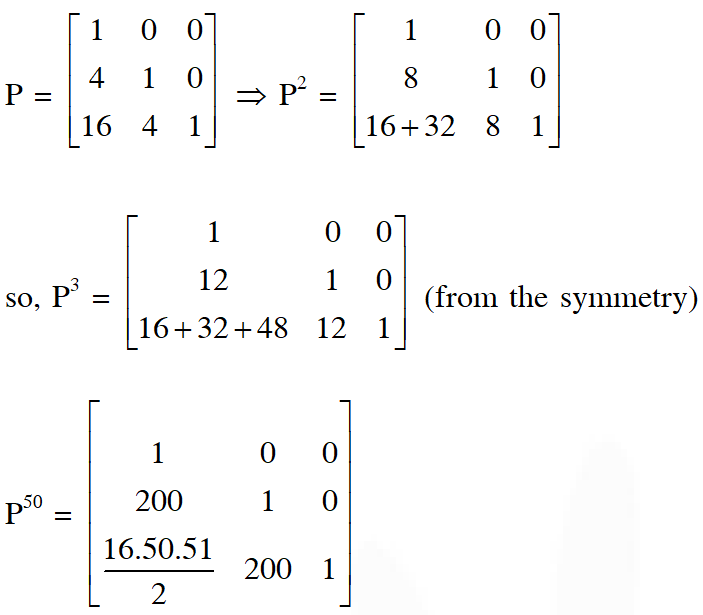
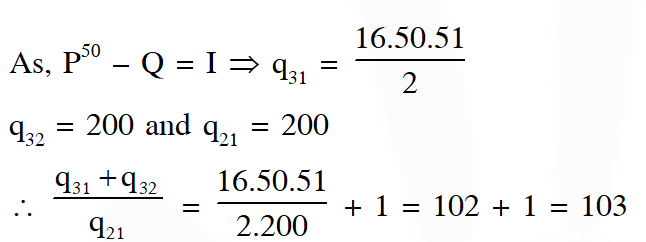
Q. Which of the following is(are) NOT the square of a 3 3 matrix with real entries ?
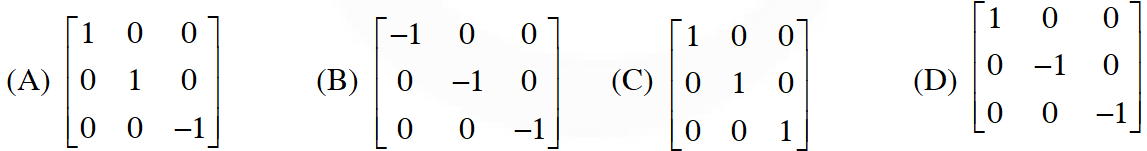[JEE(Advanced)-2017]
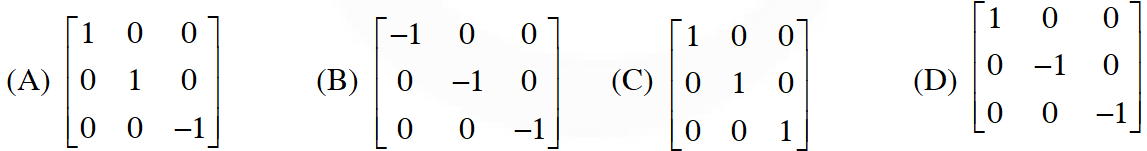[JEE(Advanced)-2017]
Ans. (A,B)
Q. How many $3 \times 3$ matrices $\mathrm{M}$ with entries from $\{0,1,2\}$ are there, for which the sum of the diagonal entries of $\mathrm{M}^{\mathrm{T}} \mathrm{M}$ is $5 ?$
(A) 198 (B) 126 (C) 135 (D) 16
[JEE(Advanced)-2017]
Ans. (A)
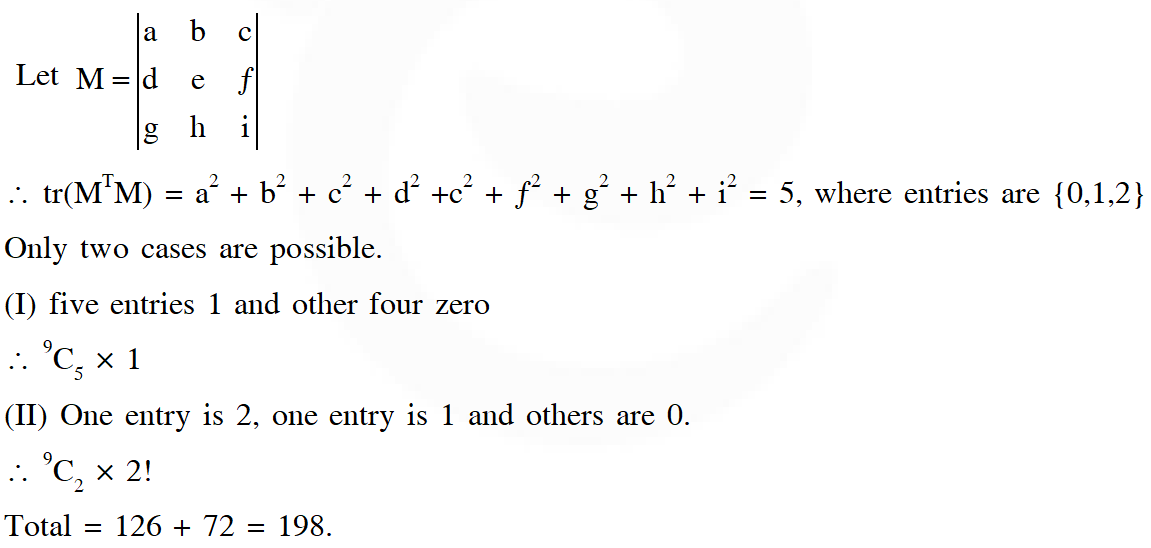
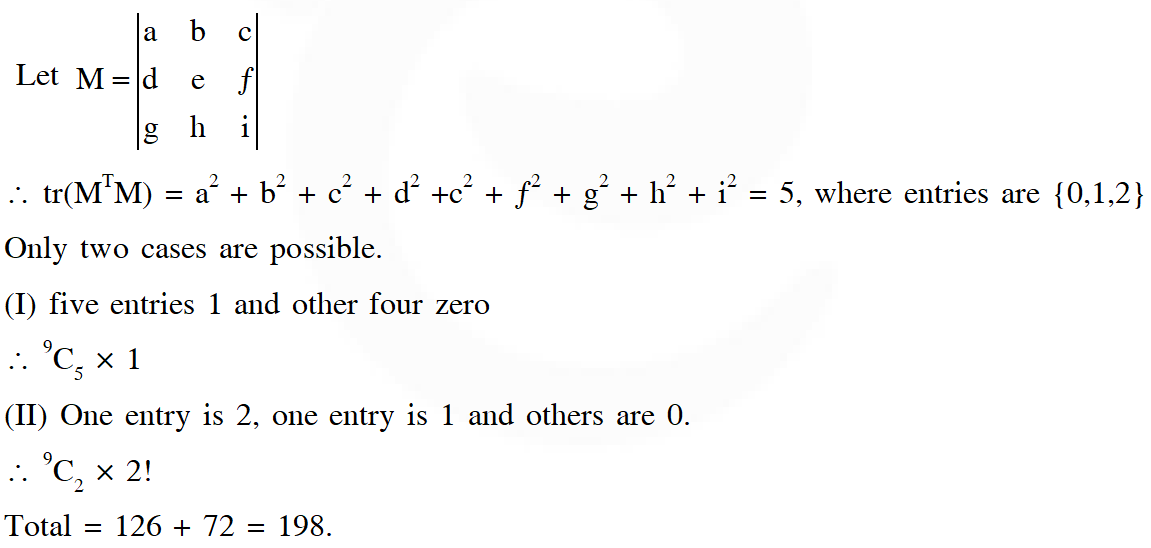
Q. Let S be the of all column matrices $\left[\begin{array}{l}{b_{1}} \\ {b_{2}} \\ {b_{3}}\end{array}\right]$ such that $b_{1}, b_{2}, b_{3} \in \square$ and the system of equations (in real variables)
$-x+2 y+5 z=b_{1}$
$2 x-4 y+3 z=b_{2}$
$x-2 y+2 z=b_{3}$
has at least one solution. Then, which of the following system(s) (in real variables) has (have) at least one solution of each $\left[\begin{array}{l}{b_{1}} \\ {b_{2}} \\ {b_{3}}\end{array}\right] \in S ?$
(A) $\mathrm{x}+2 \mathrm{y}+3 \mathrm{z}=\mathrm{b}_{1}, 4 \mathrm{y}+5 \mathrm{z}=\mathrm{b}_{2}$ and $\mathrm{x}+2 \mathrm{y}+6 \mathrm{z}=\mathrm{b}_{3}$
(B) $x+y+3 z=b_{1}, 5 x+2 y+6 z=b_{2}$ and $-2 x-y-3 z=b_{3}$
(C) $-\mathrm{x}+2 \mathrm{y}-5 \mathrm{z}=\mathrm{b}_{1}, 2 \mathrm{x}-4 \mathrm{y}+10 \mathrm{z}=\mathrm{b}_{2}$ and $\mathrm{x}-2 \mathrm{y}+5 \mathrm{z}=\mathrm{b}_{3}$
(D) $x+2 y+5 z=b_{1}, 2 x+3 z=b_{2}$ and $x+4 y-5 z=b_{3}$
[JEE(Advanced)-2018, 4(–2)]
Ans. (A,C,D)
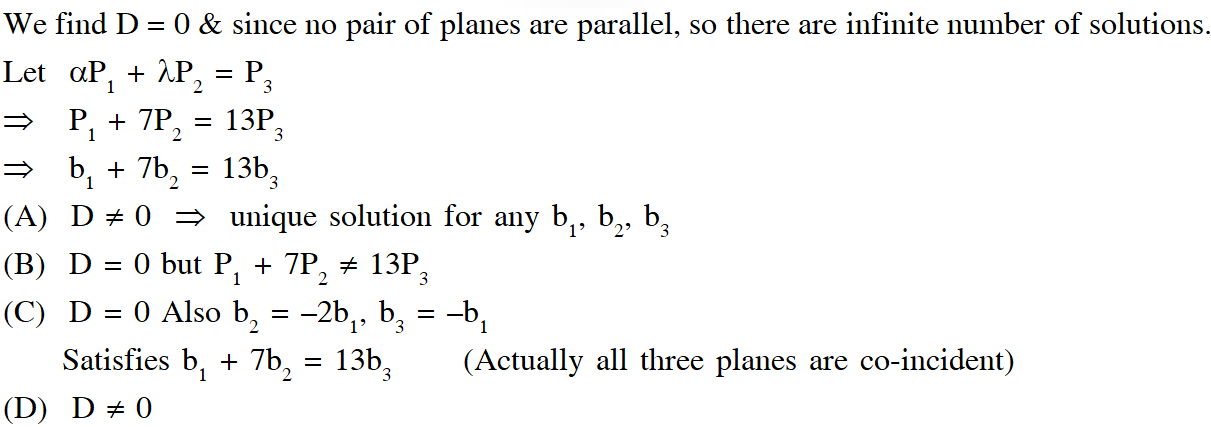
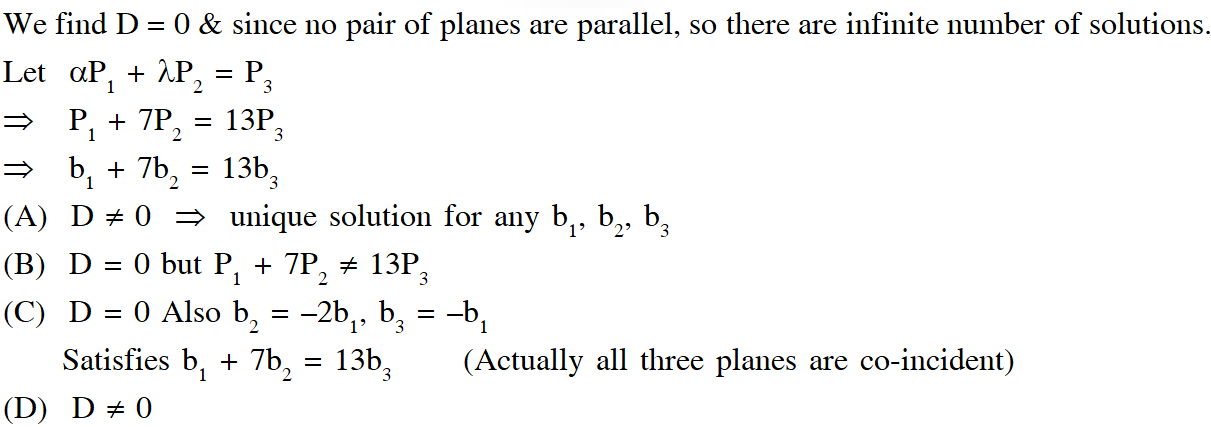
Comments
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.