JEE Main Previous Year Question of Physics with Solutions are available here. Practicing JEE Main Previous Year Papers Questions of Physics will help all the JEE aspirants in realizing the question pattern as well as help in analyzing their weak & strong areas.
Get detailed Class 11th &12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Simulator
Previous Years AIEEE/JEE Mains Questions
Q. The above is a plot of binding energy per nucleon $\mathrm{E}_{\mathrm{b}}$, against the nuclear mass M; A, B, C, D, E, F correspond to different nuclei. Consider four reactions :
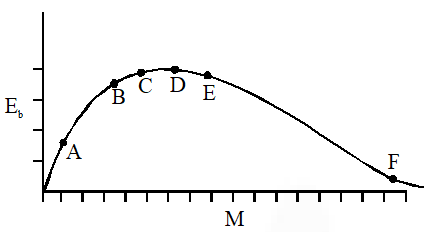(i) $\mathrm{A}+\mathrm{B} \rightarrow \mathrm{C}+\varepsilon$
(ii) $\mathrm{C} \rightarrow \mathrm{A}+\mathrm{B}+\varepsilon$
(iii) $\mathrm{D}+\mathrm{E} \rightarrow \mathrm{F}+\varepsilon$
$(\mathrm{iv}) \mathrm{F} \rightarrow \mathrm{D}+\mathrm{E}+\varepsilon$
where $\varepsilon$ is the energy released ? In which reactions is $\varepsilon$ positive ?
(1) (ii) and (iv) (2) (ii) and (iii) (3) (i) and (iv) (4) (i) and (iii)
[AIEEE - 2009]
(i) $\mathrm{A}+\mathrm{B} \rightarrow \mathrm{C}+\varepsilon$
(ii) $\mathrm{C} \rightarrow \mathrm{A}+\mathrm{B}+\varepsilon$
(iii) $\mathrm{D}+\mathrm{E} \rightarrow \mathrm{F}+\varepsilon$
$(\mathrm{iv}) \mathrm{F} \rightarrow \mathrm{D}+\mathrm{E}+\varepsilon$
where $\varepsilon$ is the energy released ? In which reactions is $\varepsilon$ positive ?
(1) (ii) and (iv) (2) (ii) and (iii) (3) (i) and (iv) (4) (i) and (iii)
[AIEEE - 2009]
Ans. (3)
Q. The speed of daughter nuclei is :-
(1) $\mathrm{c} \sqrt{\frac{\Delta \mathrm{m}}{\mathrm{M}+\Delta \mathrm{m}}}$
(2) $\mathrm{c} \frac{\Delta \mathrm{m}}{\mathrm{M}+\Delta \mathrm{m}}$
(3) $\mathrm{c} \sqrt{\frac{2 \Delta \mathrm{m}}{\mathrm{M}}}$
(4) $\mathrm{c} \sqrt{\frac{\Delta \mathrm{m}}{\mathrm{M}}}$
[AIEEE-2010]
Ans. (3)
Total kinetic energy of products
$=$ Total energy released $\frac{\mathrm{p}^{2}}{2 \mathrm{m}}+\frac{\mathrm{p}^{2}}{2 \mathrm{m}}$
$\left.=(\text { mass defect }) \mathrm{c}^{2} \text { (where } \mathrm{m}=\frac{\mathrm{M}}{2} \text { given }\right)$
$\Rightarrow 2\left(\frac{\mathrm{p}^{2}}{2 \mathrm{m}}\right)=\left[(\mathrm{M}+\Delta \mathrm{m})-\left(\frac{\mathrm{M}}{2}+\frac{\mathrm{M}}{2}\right)\right] \times \mathrm{c}^{2}$
$\Rightarrow 2 \times\left[\frac{\mathrm{p}^{2}}{2\left(\frac{\mathrm{M}}{2}\right)}\right]=(\Delta \mathrm{m}) \mathrm{c}^{2}$
$\Rightarrow \frac{2\left(\frac{\mathrm{M}}{2} \mathrm{v}\right)^{2}}{\mathrm{M}}=(\Delta \mathrm{m}) \mathrm{c}^{2} \Rightarrow \mathrm{v}=\mathrm{c} \sqrt{\frac{2 \Delta \mathrm{m}}{\mathrm{M}}}$
Q. The binding energy per nucleon for the parent nucleus is $E_{1}$ an that for the daughter nuclei is $\mathrm{E}_{2}$. Then:-
(1) $\mathrm{E}_{1}=2 \mathrm{E}_{2}$
$(2) \mathrm{E}_{2}=2 \mathrm{E}_{1}$
(3) $\mathrm{E}_{1}>\mathrm{E}_{2}$
$(4) \mathrm{E}_{2}>\mathrm{E}_{1}$
[AIEEE - 2010]
Ans. (4)
Because energy is releasing $\Rightarrow$ Binding energy per nucleon of product> that of parent $\Rightarrow \mathrm{E}_{2}>$
$\mathrm{E}_{1}$
Q. A radioactive nucleus (initial mass number A and atomic number Z) emits 3 -particles and 2 positrons. The ratio of number of neutrons to that of protons in the final nucleus will be:-
(1) $\frac{\mathrm{A}-\mathrm{Z}-4}{\mathrm{Z}-2}$
(2) $\frac{\mathrm{A}-\mathrm{Z}-8}{\mathrm{Z}-4}$
(3) $\frac{\mathrm{A}-\mathrm{Z}-4}{\mathrm{Z}-8}$
(4) $\frac{\mathrm{A}-\mathrm{Z}-12}{\mathrm{Z}-4}$
[AIEEE - 2010]
Ans. (3)
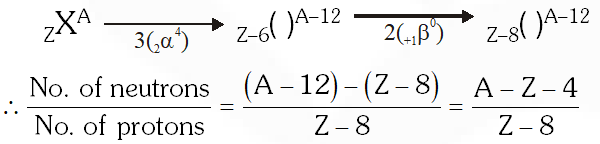
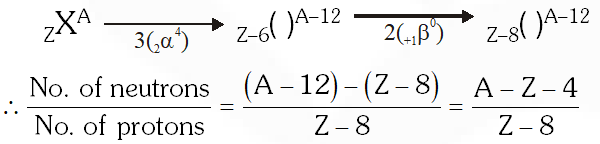
Q. After absorbing a slowly moving neutron of mass $\left.\mathrm{m}_{\mathrm{N}} \text { (momentum } \sim 0\right)$ a nucleus of mass M breaks into two nuclei of masses $\mathrm{m}_{1}$ and $5 \mathrm{m}_{1}\left(6 \mathrm{m}_{1}=\mathrm{M}+\mathrm{m}_{\mathrm{N}}\right)$, respectively. If the de Broglie wavelength of the nucleus with mass $\mathrm{m}_{1}$ is $\lambda$, then de Broglie wavelength of the other nucleus will be:-
(1) $25 \lambda$
(2) $5 \lambda$
(3) $\frac{\lambda}{5}$
( 4)$\lambda$
[AIEEE - 2011]
Ans. (4)
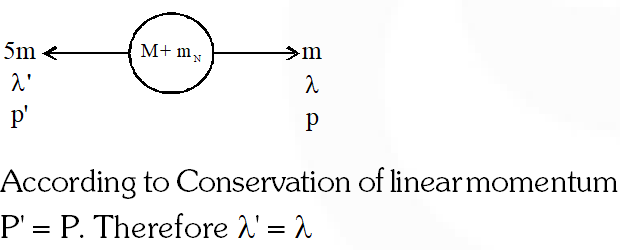
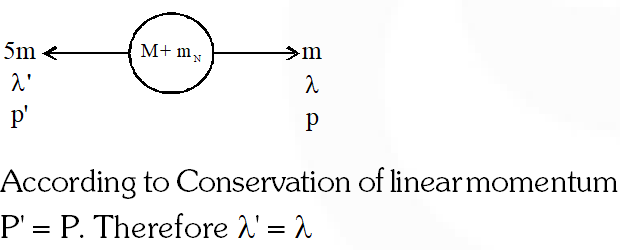
Q. Statement-1: A nucleus having energy $\mathrm{E}_{1}$ decays be $\beta^{-}$ emissionto daughter nucleus having energy $E_{2}$, but the – rays are emitted with a continuous energy spectrum having end point energy $\mathrm{E}_{1}-\mathrm{E}_{2}$.
Statement-1: To conserve energy and momentum in -decay at least three particles must take part in the transformation.
(1) Statement-1 is incorrect, statement-2 is correct
(2) Statement-1 is correct, statement-2 is incorrect
(3) Statement-1 is correct, statement-2 correct; statement-2 is the correct explanation of statement-1
(4) Statement-1 is correct, statement-2 is correct; statement -2 is not the correct explanation of statement-1.
[AIEEE - 2011]
Ans. (3)
Q. Assume that a neutron breaks into a proton and an electron. The energy released during this process is :
(Mass of neutron $=1.6725 \times 10^{-27} \mathrm{kg}$
Mass of proton $=1.6725 \times 10^{-27} \mathrm{kg}$
Mass of electron $\left.=9 \times 10^{-31} \mathrm{kg}\right)$
(1) 5.4 MeV (2) 0.73 MeV (3) 7.10 MeV (4) 6.30 MeV
[AIEEE - 2012]
Ans. (2)
Released energy
$=\left[1.6747 \times 10^{-27}-1.6725 \times 10^{-27}-9 \times 10^{-31}\right]$
$\times\left(3 \times 10^{8}\right)^{2} \mathrm{J}=0.73 \mathrm{MeV}$