JEE Main Previous Year Question of Math with Solutions are available at eSaral. Practicing JEE Main Previous Year Papers Questions of mathematics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Q. From 6 different novels and 3 different dictionaries, 4 novels and 1 dictionary are to be selected and arranged in a row on a shelf so that the dictionary is always in the middle. Then the number of such arrangements is –
(1) At least 750 but less than 1000
(2) At least 1000
(3) Less than 500
(4) At least 500 but less than 750
[AIEEE 2009]
Ans. (2)
The no. of ways to select 4 novels $\& 1$ dictionary from 6 different novels $\& 3$ different dictionary are $6 \mathrm{C}_{4} \times^{3} \mathrm{C}_{1}$
and to arrange these things in shelf so that dictionary is always in middle $-\mathrm{D}--\mathrm{are} 4 !$
Required No. of ways $^{6} \mathrm{C}_{4} \times^{3} \mathrm{C}_{1} \times 4 !=1080$
Q. There are two urns. Urn A has 3 distinct red balls and urn B has 9 distinct blue balls. From each urn two balls are taken out at random and then transferred to the other. The number of ways in which this can be done is -
(1) 3 (2) 36 (3) 66 (4) 108
[AIEEE-2010]
Ans. (4)
Urn $\mathrm{A} \rightarrow 3$ Red balls
Urn $\mathrm{B} \rightarrow 9$ Blue balls
So the number of ways $=$ selection of 2 balls from urn $\mathrm{A} \& \mathrm{B}$ each.
$=^{3} \mathrm{C}_{2} \cdot^{9} \mathrm{C}_{2}=108$
Q. Statement - 1 : The number of ways of distributing 10 identical balls in 4 distinct boxes such that no box is empty is $^{9} \mathrm{C}_{3}$
Statement - 2 : The number of ways of choosing any 3 places from 9 different places is $^{9} \mathrm{C}_{3}$
(1) Statement-1 is true, Statement-2 is false.
(2) Statement-1 is false, Statement-2 is true
(3) Statement-1 is true, Statement-2 is true; Statement-2 is a correct explanation for Statement- 1
(4) Statement-1 is true, Statement-2 is true; Statement-2 is not a correct explanation for Statement- 1
[AIEEE-2011]
Ans. (3)
$\mathrm{B}_{1}+\mathrm{B}_{2}+\mathrm{B}_{3}+\mathrm{B}_{4}=10$
$\mathrm{St}-1: \mathrm{B}_{1} \geq 1, \mathrm{B}_{2} \geq 1, \mathrm{B}_{3} \geq 1, \mathrm{B}_{4} \geq 1$
so no. of negative integers solution of equation
$\mathrm{x}_{1}+\mathrm{x}_{2}+\mathrm{x}_{3}+\mathrm{x}_{4}=10-4=6$
$6+4-1 \mathrm{C}_{4-1}=9 \mathrm{C}_{3}$
$\mathrm{St}-2:$ selction of 3 places from out of
9 places $=^{9} \mathrm{C}_{3}$
Both statements are true and correct explaination
Q. There are 10 points in a plane, out of these 6 are collinear. If N is the number of triangles formed by joining these points, then :
(1) $\mathrm{N}>190$
(2) $\mathrm{N} \leq 100$
(3) $100<\mathrm{N} \leq 140$
(4) $140<\mathrm{N} \leq 190$
[AIEEE-2011]
Ans. (2)
$\begin{aligned} \mathrm{N}=10 \mathrm{C}_{3}-^{6} \mathrm{C}_{3} &=\frac{10 \times 9 \times 8}{3 \times 2 \times 1}-\frac{6 \times 5 \times 4}{3 \times 2 \times 1} \\ &=120-20=100 \end{aligned}$
$\mathrm{N} \leq 100$
Q. Assuming the balls to be identical except for difference in colours, the number of ways in which one or more balls can be selected from 10 white, 9 green and 7 black balls is –
(1) 879 (2) 880 (3) 629 (4) 630
[AIEEE-2012]
Ans. (1)
$\mathrm{W}^{10}, \mathrm{G}^{9}, \mathrm{B}^{7}$
selection of one or more balls
$=(10+1)(9+1)(7+1)-1$
$=11 \times 10 \times 8-1=879$
Q. Let A and B be two sets containing 2 elements and 4 elements respectively. The number of subsets of A × B having 3 or more elements is
(1) 256 (2) 220 (3) 219 (4) 211
[JEE (Main)-2013]
Ans. (3)
$\mathrm{n}(\mathrm{A})=2, \mathrm{n}(\mathrm{B})=4, \mathrm{n}(\mathrm{A} \times \mathrm{B})=\mathrm{n}(\mathrm{A}) \cdot \mathrm{n}(\mathrm{B})=8$
Now subsets having 3 or more elements.
$\mathrm{S} \mathrm{C}_{3}+^{8} \mathrm{C}_{4}+\ldots .+^{8} \mathrm{C}_{8}=2^{8}-^{8} \mathrm{C}_{0}-^{8} \mathrm{C}_{1}-^{8} \mathrm{C}_{2}=256-37=219$
Q. Let $\mathrm{T}_{\mathrm{n}}$ be the number of all possible triangles formed by joining vertices of an n-sided regular polygon. If $\mathrm{T}_{\mathrm{n}+1} \mathrm{T}_{\mathrm{n}}=10,$ then the value of $\mathrm{n}$ is :
(1) 7 (2) 5 (3) 10 (4) 8
[JEE (Main)-2013]
Ans. (2)
$\mathrm{T}_{\mathrm{n}}=\mathrm{n} \mathrm{C}_{3} \Rightarrow \mathrm{n}+1 \mathrm{C}_{3}-^{\mathrm{n}} \mathrm{C}_{3}=10$
$(\mathrm{n}+1) \mathrm{n}(\mathrm{n}-1)-\mathrm{n}(\mathrm{n}-1)(\mathrm{n}-2)=60$
$\mathrm{n}(\mathrm{n}-1)=20$
$\mathrm{n}=5$
Q. The number of points, having both co-ordinates as integers, that lie in the interior of the triangle with vertices (0, 0), (0, 41) and (41, 0) is :
(1) 820 (2) 780 (3) 901 (4) 861
[JEE (Main)-2015]
Ans. (2)
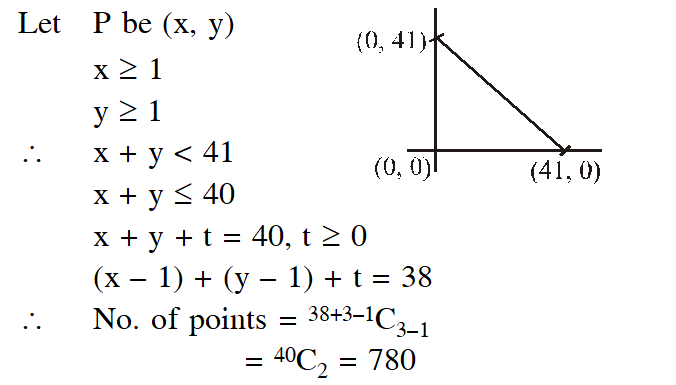
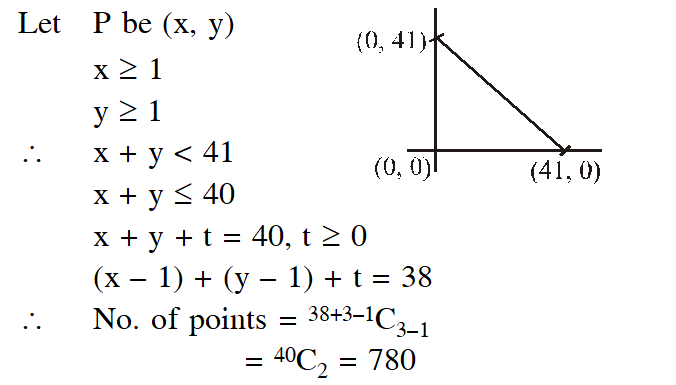
Q. Let A and B be two sets containing four and two elements respectively. Then the number of subsets of the set A × B, each having at least three elements is :
(1) 275 (2) 510 (3) 219 (4) 256
[JEE (Main)-2015]
Ans. (3)
$\mathrm{n}(\mathrm{A})=4, \mathrm{n}(\mathrm{B})=2$
$\mathrm{n}(\mathrm{A} \times \mathrm{B})=8$
Number of subsets having atleast 3 elements
$=2^{8}-\left(1+^{8} \mathrm{C}_{1}+^{8} \mathrm{C}_{2}\right)=219$
Q. The number of integers greater than 6000 that can be formed, using the digits 3,5,6,7 and 8 without repetition, is :
(1) 120 (2) 72 (3) 216 (4) 192
[JEE (Main)-2015]
Ans. (4)
Number of 4 digit numbers greater than 6000 is $\frac{3}{2} \times 4 \times 3 \times 2=72$
Number of 5 digit numbers greater than 6000 is $5 !=120$
So total number of numbers $=72+120=192$
Q. If all the words (with or without meaning) having five letters, formed using the letters of the word SMALL and arranged as in a dictionary; then the position of the word SMALL is:
[JEE (Main)-2016]
Ans. (1)
Total number of words which can be formed using all the letters of the word 'SMALL'
$=\frac{5 !}{2 !}=60$
Now, $60^{\text {th }}$ word is $\rightarrow$ SMLLA
59th word is $\rightarrow$ SMALL
58th word is $\rightarrow$ SMALL
Q. A man X has 7 friends, 4 of them are ladies and 3 are men. His wife Y also has 7 friends, 3 of them are ladies and 4 are men. Assume X and Y have no common friends. Then the total number of ways in which X and Y together can throw a party inviting 3 ladies and 3 men, so that 3 friends of each of X and Y are in this party, is :
(1) 484 (2) 485 (3) 468 (4) 469
[JEE (Main)-2017]
Ans. (2)
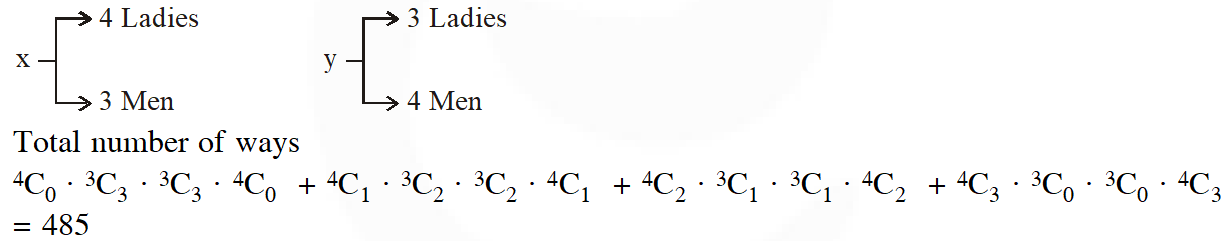
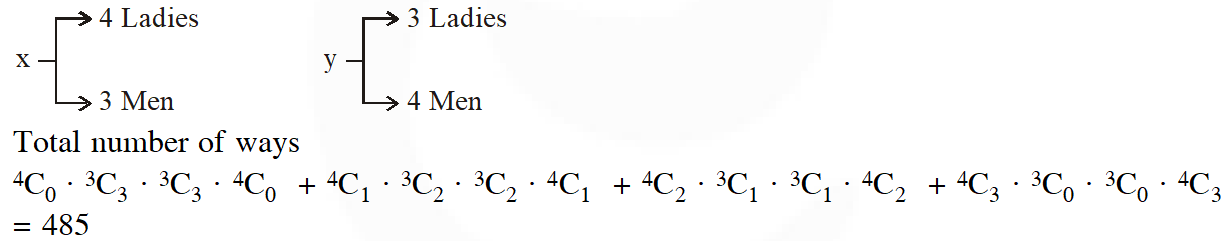
Q. From 6 different novels and 3 different dictionaries, 4 novels and 1 dictionary are to be selected and arranged in a row on a shelf so that the dictionary is always in the middle. The number of such arrangements is-
(1) less than 500
(2) at least 500 but less than 750
(3) at least 750 but less than 1000
(4) at least 1000
[JEE (Main)-2018]
Ans. (4)
$\begin{aligned} \text { Number of ways } &=\left(\begin{array}{c}{6} \\ {4}\end{array}\right)\left(\begin{array}{l}{3} \\ {1}\end{array}\right) 4 ! \\ &=15 \times 3 \times 24 \\ &=1080 \end{aligned}$
Comments
Juanita
Feb. 7, 2024, 6:46 p.m.
Wow, fantastic blog format! How lengthy have you been running
a blog for? you made running a blog glance easy. The full glance of your web site is great, as well as the content!
You can see similar: Silvoria.shop and here Silvoria.shop
canadian pharmacy online
Oct. 26, 2023, 12:47 p.m.
I've been browsing online more than 3 hours today, yet I never found any interesting article like yours. It's pretty worth enough for me. In my opinion, if all webmasters and bloggers made good content as you did, the net will be much more useful than ever before.
Manoswini panda
Feb. 16, 2021, 5:02 p.m.
Sorry it is given actually my phone is not. Working properly
