Hey, do you want to learn about the Principle of Parallel plate capacitor? If yes. Then keep reading.
 Equivalent capacitance
$C_{P}=(n-1) \frac{\varepsilon_{0} A}{d}$
Equivalent capacitance
$C_{P}=(n-1) \frac{\varepsilon_{0} A}{d}$
 The original uniform field $E_{0}$ exists in distance d-t so potential difference between the plates
The original uniform field $E_{0}$ exists in distance d-t so potential difference between the plates
$V=E_{0}(d-t)=\frac{\sigma}{\varepsilon_{0}}(d-t)$
$=\frac{Q}{\varepsilon_{0} A}(d-t)$
Capacitance $C=\frac{Q}{V}$
$=\frac{\varepsilon_{0} A}{d(1-t / d)}=\frac{C_{0}}{1-t / d}$
$c>c_{0}$ so capacitance increases on introducing a metallic slab between the plates.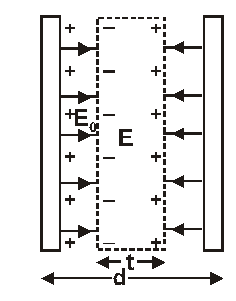
When a dielectric is introduced between plates then $\mathrm{E}_{0}$ field is present outside the dielectric and field E exists inside the dielectric. The potential difference between the plates
$V=E_{0}(d-t)+E t=E_{0}(d-t)$
$+\frac{E_{0} t}{K}=E_{0}\left[d-t\left(1-\frac{1}{K}\right)\right]$
$\mathrm{V}=\frac{\sigma}{\varepsilon_{0}}\left[\mathrm{~d}-\mathrm{t}\left(1-\frac{1}{\mathrm{~K}}\right)\right]$
$=\frac{\mathrm{Qd}}{\varepsilon_{0} \mathrm{~A}}\left[1-\frac{\mathrm{t}}{\mathrm{d}}\left(1-\frac{1}{\mathrm{~K}}\right)\right]$
Capacitance $C=\frac{Q}{V} \frac{\varepsilon_{0} A}{d\left[1-\frac{t}{d}\left(1-\frac{1}{K}\right)\right]}$
$=\frac{C_{0}}{1-\frac{t}{d}\left(1-\frac{1}{K}\right)}$
If dq charge is given to capacitor at potential V
then dW = V dq
or
$W=\int_{0}^{Q} \frac{q}{C} d q$
$\frac{Q^{2}}{2 C}=\frac{1}{2} C V^{2}=\frac{1}{2} Q V$
So, that's all from this article. If you liked this article on the Principle of Parallel plate capacitors then please share it with your friends. If you have any confusion related to this topic then feel free to ask in the comments section down below.
For a better understanding of this chapter, please check the detailed notes of the Electric charge and field. To watch Free Learning Videos on physics by Saransh Gupta sir Install the eSaral App.
Principle of Parallel plate capacitor
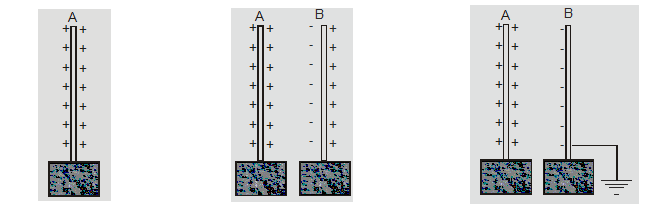
Let an insulated metal plate A be given a positive charge till its potential becomes maximum. When another insulated plate B is brought near A. Then by induction inner face of B becomes negatively charged and the outer face becomes positively charged. The negative charge tries to reduce the potential of A and the positive charge tries to increase it. When the outer surface of B is earthed positive charge flows to the earth while the negative charge stays on causing a reduction in the potential of A. Thus, a larger amount of charge can be given to A to raise it to maximum potential.
Important Points
- The capacitance of an insulated conductor is increased by bringing an uncharged earthed conductor near it.
- An arrangement of two conductors carrying equal and opposite charge separated by a dielectric medium are said to form a capacitor.
- The capacitor is an arrangement for storing a large amount of charge and hence electrical energy in a small space.
- The capacity of a capacitor is defined as the ratio of charge Q on the plates to the potential difference between the plates i.e. $C=\frac{Q}{V}$
- Capacitors are used in various electrical circuits like oscillators, in tuning circuits, filter circuits, electric fan, and motor, etc.
- The shape of conductors can be a plane, spherical or cylindrical make a parallel plate, spherical or cylindrical capacitor.
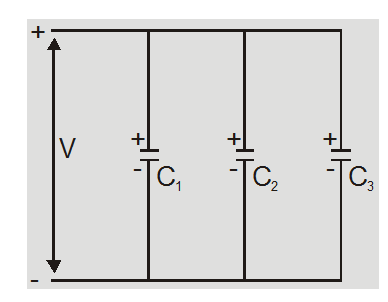
Capacitors in parallel

- Capacitors are said to be connected in parallel between two points if it is possible to proceed from one point to another point along different paths.
- Capacitors are said to be in parallel if the potential across each individual capacitor is the same and equal to the applied potential.
- Charge on each capacitor is different and is proportional to capacity of capacitor $Q \propto C$ so $\mathrm{Q}_{1}=\mathrm{C}_{1} \mathrm{~V}$ , $\mathrm{Q}_{2}=\mathrm{C}_{2} \mathrm{~V}$ , $Q_{3}=C_{3} V$
- The parallel combination obeys law of conservation of charge So
$\mathrm{Q}=\mathrm{Q}_{1}+\mathrm{Q}_{2}+\mathrm{Q}_{3}$
$=C_{1} V+C_{2} V+C_{3} V$
$=\left(C_{1}+C_{2}+C_{3}\right) V$equivalent capacitance $C_{p}=\frac{Q}{V}$
$=C_{1}+C_{2}+C_{3}$ - The equivalent capacitance may be defined as the capacitance of a single capacitor that would acquire the same total charge Q with the same potential difference V.
- The equivalent capacitance in parallel is equal to the sum of individual capacitances.
- The equivalent capacitance is greater than the largest of individual capacitances.
- The capacitors are connected in parallel (a) to increase the capacitance (b) when larger capacitance is required at low potential.
- If n identical capacitors are connected in parallel then equivalent parallel capacitance $C_{p}=n C$
- The total energy stored in parallel combination
$U=\frac{1}{2} C_{p} V^{2}$
$=\frac{1}{2}\left(\mathrm{C}_{1}+\mathrm{C}_{2}+\mathrm{C}_{3}+\ldots .\right) \mathrm{V}^{2}$
or$\mathrm{U}=\frac{1}{2} \mathrm{C}_{1} \mathrm{~V}^{2}+\frac{1}{2} \mathrm{C}_{2} \mathrm{~V}^{2}+\ldots \ldots=\mathrm{U}_{1}+\mathrm{U}_{2}$
$+U_{3}+\ldots \ldots$
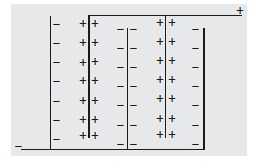
The total energy stored in parallel combination is equal to the sum of energies stored in individual capacitors. - If n plates are arranged as shown they constitute (n–1) capacitors in parallel each of capacitance $\frac{\varepsilon_{0} \mathrm{~A}}{\mathrm{~d}}$
 Equivalent capacitance
$C_{P}=(n-1) \frac{\varepsilon_{0} A}{d}$
Equivalent capacitance
$C_{P}=(n-1) \frac{\varepsilon_{0} A}{d}$
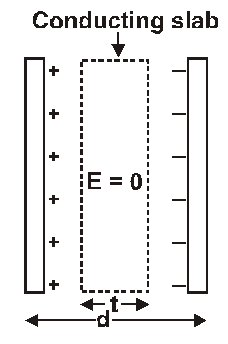
Capacitance of parallel plate capacitor with conducting slab
 The original uniform field $E_{0}$ exists in distance d-t so potential difference between the plates
The original uniform field $E_{0}$ exists in distance d-t so potential difference between the plates
$V=E_{0}(d-t)=\frac{\sigma}{\varepsilon_{0}}(d-t)$
$=\frac{Q}{\varepsilon_{0} A}(d-t)$
Capacitance $C=\frac{Q}{V}$
$=\frac{\varepsilon_{0} A}{d(1-t / d)}=\frac{C_{0}}{1-t / d}$
$c>c_{0}$ so capacitance increases on introducing a metallic slab between the plates.
The capacitance of parallel plate capacitor with dielectric slab

When a dielectric is introduced between plates then $\mathrm{E}_{0}$ field is present outside the dielectric and field E exists inside the dielectric. The potential difference between the plates
$V=E_{0}(d-t)+E t=E_{0}(d-t)$
$+\frac{E_{0} t}{K}=E_{0}\left[d-t\left(1-\frac{1}{K}\right)\right]$
$\mathrm{V}=\frac{\sigma}{\varepsilon_{0}}\left[\mathrm{~d}-\mathrm{t}\left(1-\frac{1}{\mathrm{~K}}\right)\right]$
$=\frac{\mathrm{Qd}}{\varepsilon_{0} \mathrm{~A}}\left[1-\frac{\mathrm{t}}{\mathrm{d}}\left(1-\frac{1}{\mathrm{~K}}\right)\right]$
Capacitance $C=\frac{Q}{V} \frac{\varepsilon_{0} A}{d\left[1-\frac{t}{d}\left(1-\frac{1}{K}\right)\right]}$
$=\frac{C_{0}}{1-\frac{t}{d}\left(1-\frac{1}{K}\right)}$
- $C>C_{0}$ so capacitance increases on introducing a dielectric slab between plates of capacitor.
- The capacitance is independent of position of dielectric slab between the plates.
- If whole space is filled with dielectric than t = d and $C=K C_{0}$
Energy stored in Capacitor
The charging of a capacitor involves transfer of electrons from one plate to another. The battery transfers a positive charge from negative to positive plate. Some work is done in transferring this charge which is stored as electrostatic energy in the field.If dq charge is given to capacitor at potential V
then dW = V dq
or
$W=\int_{0}^{Q} \frac{q}{C} d q$
$\frac{Q^{2}}{2 C}=\frac{1}{2} C V^{2}=\frac{1}{2} Q V$
Important Points
- The energy is stored in the electric field between plates of capacitors.
- The energy stored depends on capacitance, charge, and potential difference. This does not depend on the shape of the capacitor.
- The energy is obtained at cost of the chemical energy of the battery
So, that's all from this article. If you liked this article on the Principle of Parallel plate capacitors then please share it with your friends. If you have any confusion related to this topic then feel free to ask in the comments section down below.
For a better understanding of this chapter, please check the detailed notes of the Electric charge and field. To watch Free Learning Videos on physics by Saransh Gupta sir Install the eSaral App.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
