Question:
2 cubes each of volume $64 \mathrm{~cm}^{3}$ are joined end to end. Find the surface area of the resulting cuboid.
Solution:
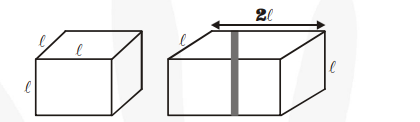
Let $\ell \mathrm{cm}$ be the length of an edge of the cube having volume $=64 \mathrm{~cm}^{3}$.
Then, $\ell^{3}=64=(4)^{3} \Rightarrow \ell=4 \mathrm{~cm}$
Now, the dimensions of the resulting cuboid made by joining two cubes (see figure) are 8 cm × 4 cm × 4 cm (i.e., length = 8 cm,
breadth $=4 \mathrm{~cm}$ and height $=4 \mathrm{~cm}$ )
Surface area of cuboid $=2(\ell b+b h+h \ell)$
= 2 (8 × 4 + 4 × 4 + 4 × 8)
$=2(32+16+32)=2 \times 80=160 \mathrm{~cm}^{2}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
