50 students enter for a school javelin throw competition. The distance (in metre) thrown are recorded below
(i) Construct a cumulative frequency table.
(ii) Draw a cumulative frequency curve (less than type) and calculate the median distance drawn by using
this curve.
(iii) Calculate the median distance by using the formula for median.
(iv) Are the median distance calculated in (ii) and (iii) same?
To draw less than type ogive, we plot the points (0, 0), (20, 6), (40,17), (60, 34), (80, 46), (100, 50), join all these points by free hand.
Now, $\frac{N}{2}=\frac{50}{2}=25$
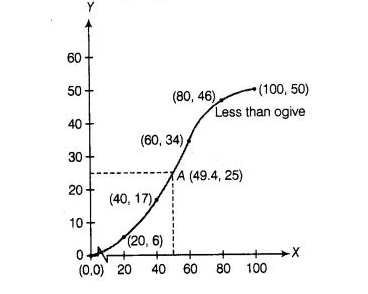
Taking Y = 25 on y-axis and draw a line parallel to X-axis, which meets the curve at point A From point A we draw a line perpendicular to X-axis,
where this meets that point is the required median i.e., 49.4.
(iii) Now, $\frac{N}{2}=\frac{50}{2}=25$
which lies is the interval $40-60$.
$\therefore \quad l=40, h=20, c f=17$ and $f=17$
$\therefore$ Median $=l+\left(\frac{\frac{N}{2}-c f}{f}\right) \times h$
$=40+\frac{(25-17)}{17} \times 20$
$=40+\frac{8 \times 20}{17}$
$=40+9.41$
$=49.41$
(lv) Yes, median distance calculated by parts (ii) and (iii) are same.