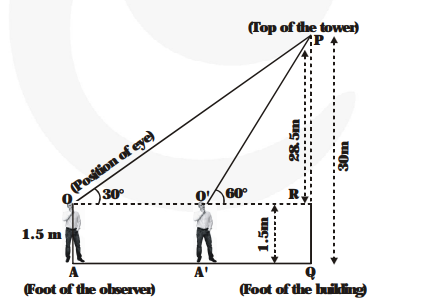
A 1.5 m tall boy is standing at some distance from a 30 m tall building

PQ = 30 m is the height of the building. OA = 1.5 m is the height of the boy. Its first position is at OA OR is horizontal line through the position of the eye at O.

$\angle \mathrm{POR}=30^{\circ}$ (Given)

The second position of the boy is at $\mathrm{O}^{\prime} \mathrm{A}^{\prime}$ and

$\angle \mathrm{PO}^{\prime} \mathrm{R}=60^{\circ} .$

Here, $\quad R Q=O A=1.5 \mathrm{~m}$

and $\quad P R=30 \mathrm{~m}-1.5 \mathrm{~m}=28.5 \mathrm{~m}$

$\Rightarrow \mathrm{OR}=28.5 \times \sqrt{\mathbf{3}} \mathrm{m} \ldots(1)$

$\Rightarrow O^{\prime} R=\frac{28.5}{\sqrt{3}} m$

The distance walked by the boy towards the building.

$=\mathrm{OO}^{\prime}=\mathrm{OR}-\mathrm{O}^{\prime} \mathrm{R}$

$=28.5 \times \sqrt{\mathbf{3}} \mathbf{m}-\frac{\mathbf{2 8 5}}{\sqrt{\mathbf{3}}} \mathbf{m}[$ From $(1)$ and $(2)]$

$=\mathbf{2 8 5} \times\left\{\sqrt{\mathbf{3}}-\frac{1}{\sqrt{\mathbf{3}}}\right\} \mathbf{m}$

$=28.5 \times \frac{(\mathbf{3}-\mathbf{1})}{\sqrt{\mathbf{3}}} \mathbf{m}=\mathbf{2 8 . 5} \times \frac{\mathbf{2}}{\sqrt{\mathbf{3}}} \mathbf{m}$

$=\frac{57}{\sqrt{3}} \mathbf{m}=19 \sqrt{3} \mathbf{m}$