A 15 high tower casts a shadow 24 Long

Let BC = 15 m be the tower and its shadow AB is 24 m. At that time ∠CAB = 8, Again, let EF = h be a telephone pole and its shadow DE = 16 m. At

the same time ∠EDF = 8 Here, ΔASC and ΔDEF both are right angled triangles.

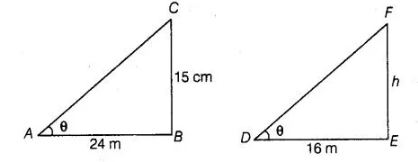
In $\triangle A B C$ and $\triangle D E F$, $\angle C A B=\angle E D F=\theta$

$\angle B=\angle E$ [each 90°]

$\therefore$ $\triangle A B C \sim \triangle D E F$ [by AAA similarity criterion]

Then, $\frac{A B}{D E}=\frac{B C}{E F}$

$\Rightarrow$ $\frac{24}{16}=\frac{15}{h}$

$\therefore$ $h=\frac{15 \times 16}{24}=10$

Hence, the height of the telephone pole is 10 m.