Question:
A 5.5m long ladder is leaned against a wall. The ladder reaches the wall to a height of 4.4m. Find^the distance between the wall and the foot
of the ladder.
Solution:
Let the distance between the wall and the foot of the ladder be $x \mathrm{~m}$
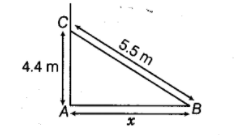
In right angled $\triangle A B C$, by using Pythagoras theorem, we get
$B C^{2}=A B^{2}+A C^{2}$
$\Rightarrow \quad(5.5)^{2}=x^{2}+(4.4)^{2}$
$\Rightarrow \quad x^{2}=(5.5)^{2}-(4.4)^{2}$
$\Rightarrow: \quad x^{2}=30.25-19.36$
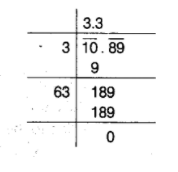
$\Rightarrow \quad x^{2}=10.89$
$\Rightarrow \quad x=\sqrt{10.89}$
$\therefore \quad x=3.3 \mathrm{~m}$
Hence, the distance between the wall and the foot of the ladder is $3.3 \mathrm{~m}$.