A and B are respectively the points on

False

Given, PQ = 12.5 cm, PA = 5 cm, BR = 6 cm and PB = 4 cm

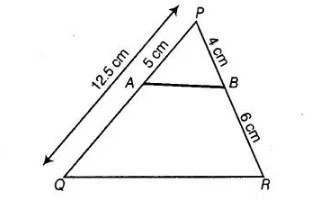
Then, $Q A=Q P-P A=12.5-5=7.5 \mathrm{~cm}$

Now, $\frac{P A}{A Q}=\frac{5}{7.5}=\frac{50}{75}=\frac{2}{3}$ $\ldots$ (i)

and $\frac{P B}{B R}=\frac{4}{6}=\frac{2}{3}$ ... (ii)

From Eqs. (i) and (ii), $\frac{P A}{A Q}=\frac{P B}{B R}$

By converse of basic proportionality theorem,

$A B \| Q R$