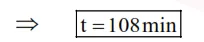A and B decompose via first order kinetics with half-lives $54.0 \mathrm{~min}$ and $18.0 \mathrm{~min}$ respectively. Starting from an equimolar non reactive mixture of $\mathrm{A}$ and $\mathrm{B}$, the time taken for the concentration of A to become 16 times that of B is min. (Round off to the Nearest Integer).
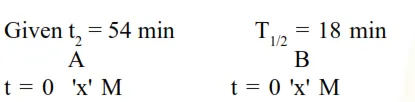
$\Rightarrow$ To calculate : $\left[\mathrm{A}_{\mathrm{t}}\right]=16 \times\left[\mathrm{B}_{\mathrm{t}}\right] \ldots . .(1)$ time $=?$

$\mathrm{n} \rightarrow$ no of Half lives
$\Rightarrow$ Now from the relation (1)
$\left[\mathrm{A}_{\mathrm{t}}\right]=16 \times\left[\mathrm{B}_{\mathrm{t}}\right]$
$\Rightarrow \quad \frac{\mathrm{x}}{(2)^{\mathrm{n}_{1}}}=\frac{\mathrm{x}}{(2)^{\mathrm{n}_{2}}} \times 16 \Rightarrow(2)^{\mathrm{n}_{2}}=(2)^{\mathrm{n}_{1}} \times(2)^{4}$
$\Rightarrow \mathrm{n}_{2}=\mathrm{n}_{1}+4 \quad \Rightarrow \quad \frac{\mathrm{t}}{\left(\mathrm{t}_{1 / 2}\right)_{2}}=\frac{\mathrm{t}}{\left(\mathrm{t}_{1 / 2}\right)_{1}}+4$
$\Rightarrow \quad \mathrm{t}\left(\frac{1}{18}-\frac{1}{54}\right)=4 \Rightarrow \mathrm{t}=\frac{4 \times 18 \times 54}{36}$