A B C D is a parallelogram and X is the mid-point

False

Given, $A B C D$ is a parallelogram and ar $(A X C D)=24 \mathrm{~cm}^{2}$

Let area of parallelogram $A B C D$ is $2 y \mathrm{~cm}^{2}$ and join $A C$.

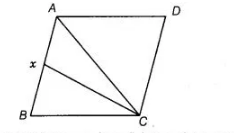
We know that, diagonal divides the area of parallelogram in two equal areas.

$\therefore \quad \operatorname{ar}(\Delta A B C)=\operatorname{ar}(A C D)=y \quad$ [say]

Also, $X$ is the mid-point of $A B$.

So, $\operatorname{ar}(\Delta A C X)=\operatorname{ar}(B C X)$ [since, $X$ is median in $\triangle A B C$ ]

$=\frac{1}{2} \operatorname{ar}(A B C)=\frac{1}{2} y$

Now, ar $(A X C D)=\operatorname{ar}(\triangle A D C)+\operatorname{ar}(A C X)$

$24=y+\frac{y}{2}$ [given]

$\Rightarrow$ $24=\frac{3 y}{2}$

$\Rightarrow$ $y=\frac{24 \times 2}{3}=16 \mathrm{~cm}^{2}$

Hence, $\operatorname{ar}(\Delta A B C)=16 \mathrm{~cm}^{2}$

Therefore, given statement is false.