$A B C D$ is a rhombus such that $\angle A C B=40^{\circ}$, then $\angle A D B$ is
(a) $40^{\circ}$
(b) $45^{\circ}$
(c) $50^{\circ}$
(d) $60^{\circ}$
(c) Given, $A B C D$ is a rhombus such that $\angle A C B=40^{\circ} \Rightarrow \angle O C B=40^{\circ}$
Since, $A D \| B C$
$\angle D A C=\angle B C A=40^{\circ}$ [alternate interior angles]
Also, $\angle A O D=90^{\circ}$
[diagonals of a rhombus are perpendicular to each other]
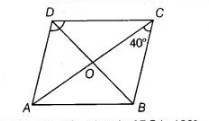
We know that, sum of all angles of a triangle $A D O$ is $180^{\circ}$.
$\therefore \quad \angle A D O+\angle D O A+\angle O A D=180^{\circ}$
$\angle A D O=180^{\circ}-\left(40^{\circ}+90^{\circ}\right)$
$=180^{\circ}-130^{\circ}=50^{\circ}$
$\Rightarrow \quad \angle A D B=50^{\circ}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
