Question.
A ball is dropped from a height of $90 \mathrm{~m}$ on a floor. At each collision with the floor, the ball loses one tenth of its speed. Plot the speed-time graph of its motion between $t=0$ to $12 \mathrm{~s} .$
A ball is dropped from a height of $90 \mathrm{~m}$ on a floor. At each collision with the floor, the ball loses one tenth of its speed. Plot the speed-time graph of its motion between $t=0$ to $12 \mathrm{~s} .$
solution:
Ball is dropped from a height, s = 90 m
Initial velocity of the ball, $u=0$
Acceleration, $a=g=9.8 \mathrm{~m} / \mathrm{s}^{2}$
Final velocity of the ball $=v$
From second equation of motion, time $(t)$ taken by the ball to hit the ground can be obtained as:
$s=u t+\frac{1}{2} a t^{2}$
$90=0+\frac{1}{2} \times 9.8 t^{2}$
$t=\sqrt{18.38}=4.29 \mathrm{~s}$
From first equation of motion, final velocity is given as:
$v=u+a t$
$=0+9.8 \times 4.29=42.04 \mathrm{~m} / \mathrm{s}$
Rebound velocity of the ball, $u_{\mathrm{r}}=\frac{9}{10} v=\frac{9}{10} \times 42.04=37.84 \mathrm{~m} / \mathrm{s}$
Time $(t)$ taken by the ball to reach maximum height is obtained with the help of first equation of motion as:
$v=u_{r}+a t^{\prime}$
$0=37.84+(-9.8) t$
$t^{\prime}=\frac{-37.84}{-9.8}=3.86 \mathrm{~s}$
Total time taken by the ball $=t+t^{\prime}=4.29+3.86=8.15 \mathrm{~s}$
As the time of ascent is equal to the time of descent, the ball takes $3.86 \mathrm{~s}$ to strike back on the floor for the second time.
The velocity with which the ball rebounds from the floor $=\frac{9}{10} \times 37.84=34.05 \mathrm{~m} / \mathrm{s}$
Total time taken by the ball for second rebound $=8.15+3.86=12.01 \mathrm{~s}$
The speed-time graph of the ball is represented in the given figure as: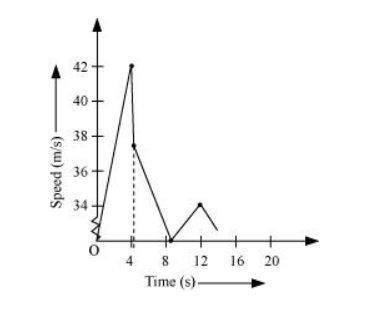
Ball is dropped from a height, s = 90 m
Initial velocity of the ball, $u=0$
Acceleration, $a=g=9.8 \mathrm{~m} / \mathrm{s}^{2}$
Final velocity of the ball $=v$
From second equation of motion, time $(t)$ taken by the ball to hit the ground can be obtained as:
$s=u t+\frac{1}{2} a t^{2}$
$90=0+\frac{1}{2} \times 9.8 t^{2}$
$t=\sqrt{18.38}=4.29 \mathrm{~s}$
From first equation of motion, final velocity is given as:
$v=u+a t$
$=0+9.8 \times 4.29=42.04 \mathrm{~m} / \mathrm{s}$
Rebound velocity of the ball, $u_{\mathrm{r}}=\frac{9}{10} v=\frac{9}{10} \times 42.04=37.84 \mathrm{~m} / \mathrm{s}$
Time $(t)$ taken by the ball to reach maximum height is obtained with the help of first equation of motion as:
$v=u_{r}+a t^{\prime}$
$0=37.84+(-9.8) t$
$t^{\prime}=\frac{-37.84}{-9.8}=3.86 \mathrm{~s}$
Total time taken by the ball $=t+t^{\prime}=4.29+3.86=8.15 \mathrm{~s}$
As the time of ascent is equal to the time of descent, the ball takes $3.86 \mathrm{~s}$ to strike back on the floor for the second time.
The velocity with which the ball rebounds from the floor $=\frac{9}{10} \times 37.84=34.05 \mathrm{~m} / \mathrm{s}$
Total time taken by the ball for second rebound $=8.15+3.86=12.01 \mathrm{~s}$
The speed-time graph of the ball is represented in the given figure as:

Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
