A beam is supported at its ends by supports which are 12 m apart

Solution:

Given: A beam is supported at its ends by supports which are 12 m apart. There is a deflection of 3 cm at the center, and the deflected beam is in the shape of a parabola.

Need to find: How far from the center is the deflection 1 cm

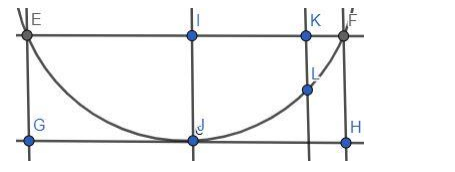
Here EF are the ends of the beam and they are $12 \mathrm{~m}$ apart.

$\mathrm{IJ}$ is the deflection of $3 \mathrm{~cm}$ at the center.

We know, that the distance $\mathrm{IF}=\frac{12}{2}=6 \mathrm{~m}=600 \mathrm{~cm}$ and the deflection $\mathrm{IJ}=\mathrm{FH}=3 \mathrm{~cm}$.

So, the coordinate of the point $F$ is $(600,3)$

Let, the equation of the parabola is: $x^{2}=4 a y$

F point is on the parabola. So, putting the coordinates of $F$ in the equation we get,

$x^{2}=4 a y$

$\Rightarrow 3600=4 a \times 3$

$\Rightarrow a=300$

Here KL denotes the deflection of $1 \mathrm{~cm}$.

So, at the point $L$ the value of $y$-coordinate is $(3-1)=2$

So, by the equation,

$\Rightarrow x^{2}=4 a y=4 \times 300 \times 2=2400$

$\Rightarrow x=49 \mathrm{~cm}$

So, the distance of the point of $1 \mathrm{~cm}$ deflection from the center is $49 \mathrm{~cm}$.