A boat goes 12 km upstream and 40 km downstream in 8 hours.

We have to find the speed of the boat in still water and speed of the stream

Let the speed of the boat in still water be II $\mathrm{km} / \mathrm{hr}$ and the speed of the stream be $=\mathrm{km} / \mathrm{hr}$ then

Speed upstream $=(x-y) \mathrm{kn} / \mathrm{hr}$

Sped down stream $=(x+y) \mathrm{km} / \mathrm{hr}$

\text { Now, Time taken to cover } 12 \mathrm{~km} \text { upstream }=\frac{12}{x-y} h r s

Time taken to cover $40 \mathrm{~km}$ down stream $=\frac{40}{x+y} h r s$

But, total time of journey is 8 hours

$\frac{12}{x-y}+\frac{40}{x+y}=8 \cdots(i)$

Time taken to cover $16 \mathrm{~km}$ upstream $=\frac{16}{x-y} h r s$

Time taken to cover $32 \mathrm{~km}$ down stream $=\frac{32}{x+y} h r s$

In this case total time of journey is given to $8 h r s$

$\frac{16}{(x-y)}+\frac{32}{(x+y)}=8$...(ii)

By $\frac{1}{x-y}=u$ and $\frac{1}{x+y}=v$ in equation (i) and (ii) we get

$12 u+40 v=8$

$16 u+32 v=8$

$12 u+40 v-8=0 \cdots($ iii $)$

$16 u+32 v-8=0 \cdots($ iv $)$

Solving these equations by cross multiplication we get

$\frac{u}{40 \times-8-32 \times-8}=\frac{-v}{12 \times-8-16 \times-8}=\frac{1}{12 \times 32-16 \times 40}$

$\frac{u}{-320+256}=\frac{-v}{-96+128}=\frac{1}{384-640}$

$\frac{u}{-64}=\frac{-v}{32}=\frac{1}{-256}$

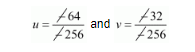
$u=\frac{1}{4}$ and $v=\frac{1}{8}$

Now,

$u=\frac{1}{x-y}$

$\frac{1}{x-y}=\frac{1}{4}$

$4=x-y \cdots(v)$

and

$v=\frac{1}{x+y}$

$\frac{1}{x+y}=\frac{1}{8}$

$x+y=8 \cdots(v i)$

By solving equation $(v)$ and $(v i)$ we get,

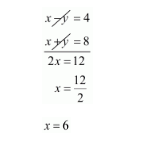
By substituting $x=6$ in equation (vi) we get

$x+y=8$

$6+y=8$

$y=8-6$

$y=2$

Hence, the speed of boat in still water is $6 \mathrm{~km} / \mathrm{hr}$,

The speed of the stream is $2 \mathrm{~km} / \mathrm{hr}$.