A boy is standing on the ground and flying a kite with 100 m of string at an elevation of 30°. Another boy is sanding on the roof of a 10 m high building and is flying his kite at an elevation of 45°. Both the boys are on opposite sides of both the kites. Find the length of the string that the second boy must have so that the two kites meet.
Let 
be the string of string 
m. let 
be the ground and a boy flying kite of 
m string at an elevation of
.And another boy flying kite of 10 m high building at an angle of elevation
.
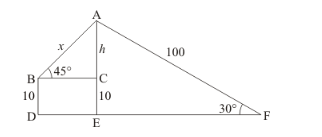
Let $A E=H, A C=h, C E=10, A B=x$, and $A F=100 \mathrm{~m} . \angle A B C=45^{\circ}, \angle A F E=30^{\circ}$
Here we have to find length of string.
We use trigonometric ratios.
In ΔAFE,
$\Rightarrow \sin 30^{\circ}=\frac{A E}{A F}$
$\Rightarrow \frac{1}{2}=\frac{H}{100}$
$\Rightarrow H=50$
$\Rightarrow h=H-10$
$\Rightarrow h=50-10$
$\Rightarrow h=40$
Again in ΔABC,
$\Rightarrow \sin 45^{\circ}=\frac{A B}{A C}$
$\Rightarrow \frac{1}{\sqrt{2}}=\frac{h}{x}$
$\Rightarrow \frac{1}{\sqrt{2}}=\frac{40}{x}$
$\Rightarrow x=40 \sqrt{2}$
Hence the length of string is $40 \sqrt{2}$.