A butterfly is flying with a velocity $4 \sqrt{2} \mathrm{~m} / \mathrm{s}$ in North-East direction. Wind is slowly blowing at $1 \mathrm{~m} / \mathrm{s}$ from North to South. The resultant displacement of the butterfly in 3 seconds is :
Correct Option: , 4
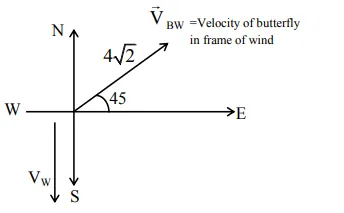
$\vec{V}_{B W}=4 \sqrt{2} \cos 45 \hat{i}+4 \sqrt{2} \sin 45 \hat{j}$
$=4 \hat{i}+4 \hat{j}$
$\overrightarrow{\mathrm{V}}_{\mathrm{W}}=-\hat{\mathrm{j}}$
$\overrightarrow{\mathrm{V}}_{\mathrm{B}}=\overrightarrow{\mathrm{V}}_{\mathrm{BW}}+\overrightarrow{\mathrm{V}}_{\mathrm{W}}=4 \hat{\mathrm{i}}+3 \hat{\mathrm{j}}$
$\overrightarrow{\mathrm{S}}_{\mathrm{B}}=\overrightarrow{\mathrm{V}}_{\mathrm{B}} \times \mathrm{t}=(4 \hat{\mathrm{i}}+3 \hat{\mathrm{j}}) \times 3=12 \hat{\mathrm{i}}+9 \hat{\mathrm{j}}$
$\left|\vec{S}_{\mathrm{B}}\right|=\sqrt{(12)^{2}+(9)^{2}}=15 \mathrm{~m}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.