A capillary tube made of glass of radius $0.15 \mathrm{~mm}$ is dipped vertically in a beaker filled with methylene iodide (surface tension $=0.05 \mathrm{Nm}^{-1}$, density $=667 \mathrm{~kg} \mathrm{~m}^{-3}$ ) which rises to height $h$ in the tube. It is observed that the two tangents drawn from liquid-glass interfaces (from opp. sides of the capillary) make an angle of $60^{\circ}$ with one another. Then $h$ is close to $\left(g=10 \mathrm{~ms}^{-2}\right)$.
Correct Option: , 2
(2) Given,
Angle of contact $\theta=30^{\circ}$
Surface tension, $T=0.05 \mathrm{Nm}^{-1}$
Radius of capillary tube, $r=0.15 \mathrm{~mm}=0.15 \times 10^{-3} \mathrm{~m}$
Density of methylene iodide, $\rho=667 \mathrm{~kg} \mathrm{~m}^{-3}$
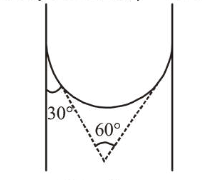
Capillary rise, $h=\frac{2 T \cos \theta}{\rho g r}$
$=\frac{2 \times 0.05 \times \frac{\sqrt{3}}{2}}{667 \times 10 \times 0.15 \times 10^{-3}}=0.087 \mathrm{~m}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.