A car weighs 1800 kg.

solution:

Mass of the car, m = 1800 kg

Distance between the front and back axles, d = 1.8 m

Distance between the C.G. (centre of gravity) and the back axle = 1.05 m

The various forces acting on the car are shown in the following figure.



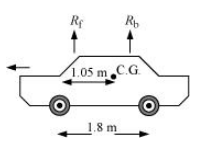
$R_{\mathrm{f}}$ and $R_{\mathrm{b}}$ are the forces exerted by the level ground on the front and back wheels respectively.

At translational equilibrium:

$R_{\mathrm{f}}+R_{\mathrm{b}}=m g$

$=1800 \times 9.8$

$=17640 \mathrm{~N} \ldots(i)$

For rotational equilibrium, on taking the torque about the C. G., we have:

$R_{\mathrm{f}}(1.05)=R_{\mathrm{b}}(1.8-1.05)$

$R_{\mathrm{f}} \times 1.05=R_{\mathrm{b}} \times 0.75$

$\frac{R_{\mathrm{f}}}{R_{\mathrm{b}}}=\frac{0.75}{1.05}=\frac{5}{7}$

$\frac{R_{\mathrm{b}}}{R_{\mathrm{f}}}=\frac{7}{5}$

$R_{\mathrm{b}}=1.4 R_{\mathrm{f}}$ $\ldots(i i)$

Solving equations $(i)$ and $(i i)$, we get:

$1.4 R_{\mathrm{f}}+R_{\mathrm{f}}=17640$

$R_{\mathrm{f}}=\frac{17640}{2.4}=7350 \mathrm{~N}$

$\therefore R_{b}=17640-7350=10290 \mathrm{~N}$

Therefore, the force exerted on each front wheel $=\frac{7350}{2}=3675 \mathrm{~N}$, and

The force exerted on each back wheel $=\frac{10290}{2}=5145 \mathrm{~N}$